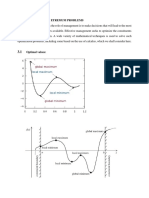
Chapter 8, Section 3 Handout We are now ready to undertake a brief but useful look at local maxima and minima

for functions of the type z = f ( x, y ) . We will be extending the second-derivative test we learned in Chapter 5; a little more work is involved since we are dealing with multivariable functions, but yet the technique is similar. The most challenging part about the second-derivative test, when dealing with multivariable functions is finding the critical values. When we found critical values in Chapter 5, we found the partition numbers of the first derivative that fit into the domain of the original function. We have a similar technique but, we must find the partition numbers of both first-order partial derivatives, simultaneously. (In other words, we will be finding the points of intersection for the first-order partial derivatives.) The critical points are called points now instead of values, because we are dealing with multivariable functions that have both x and y coordinates. Once we find the critical points for a multivariable function, now we go on to determine where we have local extrema. LOCAL EXTREMA AND PARTIAL DERIVATIVES: Let f ( a, b ) be a local extremum (a local max or a local min) for the function f. If both f x and f y exist at ( a, b ) , then f x ( a, b ) = 0 and f y ( a, b ) = 0 . SECOND-DERIVATIVE TEST FOR LOCAL EXTREMA OF MULTIVARIABLE FUNCTIONS: Given: 1. z = f ( x, y ) 2. f x ( a, b ) = 0 and f y ( a, b ) = 0 [ ( a, b ) is a critical point] 3. All second-order partial derivatives of f exist in some circular region containing (a, b) as a center. 4. A = f xx ( a, b ) , B = f xy ( a, b ) , C = f yy ( a, b ) Then: Case 1. If AC B 2 > 0 and A < 0, then f ( a, b ) is a local maximum. Case 2. If AC B 2 > 0 and A > 0, then f ( a, b ) is a local minimum. Case 3. If AC B 2 < 0 , then f (a, b) is a saddle point which is neither a max nor a min. Case 4. If AC B 2 = 0, the test fails.

PICTURES OF MAX, MIN, AND SADDLE POINT