Professional Documents
Culture Documents
Random Fractals: Logan Axon
Uploaded by
Babai KunduOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Random Fractals: Logan Axon
Uploaded by
Babai KunduCopyright:
Available Formats
Random fractals
Logan Axon
Notre Dame
March 29, 2010
Introduction
What is a fractal?
There is no universally agreed upon denition of fractal. Mandelbrot
took the from the Latin fractus meaning broken. He used it to describe
sets that were too badly behaved for traditional geometry.
Outline
1
Bad behavior by example
2
Fractal dimension
3
Random fractals
Logan Axon (Notre Dame) Random fractals March 29, 2010 2 / 36
The Cantor middle thirds set
Start with the unit interval [0, 1]. Remove the middle third to get
_
0,
1
3
_
2
3
, 1
. Continue removing middle thirds. The Cantor set C is
what is left.
0 1
.
.
.
C
Logan Axon (Notre Dame) Random fractals March 29, 2010 3 / 36
The Cantor middle thirds set
In symbols . . .
E
0
= [0, 1]
E
1
=
_
0,
1
3
_
_
2
3
, 1
_
E
2
=
_
0,
1
9
_
_
2
9
,
1
3
_
_
2
3
,
7
9
_
_
8
9
, 1
_
.
.
.
C =
i =0
E
i
0 1
.
.
.
C
Exercise
What is the total length of all the intervals removed in the construction of
C?
Logan Axon (Notre Dame) Random fractals March 29, 2010 4 / 36
Properties of the Cantor set C
1
It is self-similar: The part of C in
_
0,
1
3
is a scaled copy of all of C.
2
It has detail at all scales.
3
It is simple to dene but hard to describe geometrically.
4
Its local geometry is strange: every open interval containing one
point of C must contain other points of C as well as points not in C.
All fractals should have these properties.
Logan Axon (Notre Dame) Random fractals March 29, 2010 5 / 36
The von Koch curve
0) Begin with a unit line.
1) Replace the middle third with
the top of an equilateral
triangle.
2) Replace the middle third of each
of the 4 line segments.
.
.
.
The result is a continuous, nowhere
dierentiable curve with innite
length called the von Koch curve.
.
.
.
Logan Axon (Notre Dame) Random fractals March 29, 2010 6 / 36
The von Koch curve
Logan Axon (Notre Dame) Random fractals March 29, 2010 7 / 36
Generalizations of the von Koch curve
The construction of the von Koch curve can be modied in a number of
ways.
The quadratic von Koch curve or Minkowski sausage:
Logan Axon (Notre Dame) Random fractals March 29, 2010 8 / 36
The dragon curve
Image source: Wikipedia
Logan Axon (Notre Dame) Random fractals March 29, 2010 9 / 36
The Mandelbrot set
Image source: http://www.math.utah.edu/
~
pa/math/mandelbrot/mandelbrot.html
Constructed by looking at iterations of a function on C. We wont deal
with this kind of fractal.
Logan Axon (Notre Dame) Random fractals March 29, 2010 10 / 36
Dimension of a fractal
One of the main tools in fractal geometry is fractal dimension.
Warning: There are a lot of dierent ways to dene fractal dimension
(Hausdor dimension is the most widely used). Our denition is almost
Hausdor dimension but only works for certain kinds of fractals.
Idea
Look at covering the fractal with smaller and smaller sets. As the sets get
smaller we need more of them to cover the fractal. Measure how fast the
number of sets increases as the size of the sets decreases.
Logan Axon (Notre Dame) Random fractals March 29, 2010 11 / 36
Covering the Cantor set
The construction of the Cantor set shows how to cover it with smaller and
smaller sets.
We can cover C with:
0 1
.
.
.
0) 1 set of size 1;
1) 2 sets of size
1
3
;
2) 4 sets of size
1
9
;
.
.
.
n) 2
n
sets of size . . .
3
n
.
Logan Axon (Notre Dame) Random fractals March 29, 2010 12 / 36
Covering the Cantor set
The construction of the Cantor set shows how to cover it with smaller and
smaller sets.
We can cover C with:
0 1
.
.
.
0) 1 set of size 1;
1) 2 sets of size
1
3
;
2) 4 sets of size
1
9
;
.
.
.
n) 2
n
sets of size . . . 3
n
.
Logan Axon (Notre Dame) Random fractals March 29, 2010 12 / 36
Fractal dimension of the Cantor set
We want to measure how fast 2
n
grows relative to how fast 3
n
shrinks.
Do this by looking at
lim
n
3
nx
2
n
for dierent values of x.
lim
n
3
nx
(2
n
) = lim
n
_
2 3
x
_
n
=
_
_
if 2 3
x
> 1
1 if 2 3
x
= 1
0 if 2 3
x
< 1
Logan Axon (Notre Dame) Random fractals March 29, 2010 13 / 36
Fractal dimension of the Cantor set
We want to measure how fast 2
n
grows relative to how fast 3
n
shrinks.
Do this by looking at
lim
n
3
nx
2
n
for dierent values of x.
lim
n
3
nx
(2
n
) = lim
n
_
2 3
x
_
n
=
_
_
if 2 3
x
> 1
1 if 2 3
x
= 1
0 if 2 3
x
< 1
Logan Axon (Notre Dame) Random fractals March 29, 2010 13 / 36
Fractal dimension of the Cantor set
8
d
x
0
1
y = lim
n
3
nx
2
n
The fractal dimension of the Cantor set is the value d where
lim
n
3
nx
(2
n
) switches from to 0. This happens when 2 3
x
= 1.
Logan Axon (Notre Dame) Random fractals March 29, 2010 14 / 36
Fractal dimension of the Cantor set
2 3
x
= 1 2 = 3
x
log 2 = x log 3
x =
log 2
log 3
Therefore the fractal dimension of the Cantor set is
log 2
log 3
0.6309.
We wish to do this more generally. We wont always be covering with
straight line segments so we need a good denition for the size of a more
general set.
Logan Axon (Notre Dame) Random fractals March 29, 2010 15 / 36
Fractal dimension of the Cantor set
2 3
x
= 1 2 = 3
x
log 2 = x log 3
x =
log 2
log 3
Therefore the fractal dimension of the Cantor set is
log 2
log 3
0.6309.
We wish to do this more generally. We wont always be covering with
straight line segments so we need a good denition for the size of a more
general set.
Logan Axon (Notre Dame) Random fractals March 29, 2010 15 / 36
Diameter
Denition
The diameter of a set is the largest distance between two points in the set.
To be technically correct, the diameter of a set is the supremum of the
distances between two points in the set.
For example:
The diameter of the line segment [0, 1] is 1;
The diameter of a triangle is the length of its longest side;
The diameter of a rectangle is the length of its diagonal;
The diameter of a disk is twice the radius.
Logan Axon (Notre Dame) Random fractals March 29, 2010 16 / 36
Fractal dimension
Suppose N
is the minimum number of sets of diameter needed to cover
the set F. We compare how fast N
grows relative to the how fast
shrinks by looking at
lim
0+
x
N
.
8
m
d
x
0
y = lim
0+
x
N
Logan Axon (Notre Dame) Random fractals March 29, 2010 17 / 36
Fractal dimension
The fractal dimension of F is the value d where lim
0+
x
N
switches
from to 0.
8
m
d
x
0
In symbols:
d = inf
_
x : lim
0+
x
N
= 0
_
The actual value lim
0+
d
N
may be 0, , or anything in between.
This value is called the d-dimensional measure of the set.
Logan Axon (Notre Dame) Random fractals March 29, 2010 18 / 36
Why dimension?
Why is this called fractal dimension?
It agrees with our ideas of what dimension should be:
The fractal dimension of a point is 0;
The fractal dimension of a line is 1;
.
.
.
And the fractal dimension of the Cantor set is 0.6309. The Cantor set
had properties between those of a point and a line. It makes sense that
the fractal dimension of the Cantor set is between 0 and 1.
Logan Axon (Notre Dame) Random fractals March 29, 2010 19 / 36
Fractal dimension of the von Koch curve
Generalize the technique from the calculation for C. Again the
construction tells us how to get covers of the curve.
We can cover the curve with:
(0) 1 full-sized copy of the curve;
(1) 4 copies of the curve scaled by
1
3
;
(2) 16 copies of the curve scaled by
1
9
;
.
.
.
(n) 4
n
copies of the curve scaled by
3
n
.
The diameter of the curve itself is 1. So . . .
Logan Axon (Notre Dame) Random fractals March 29, 2010 20 / 36
Bestiary
The dimension of a point is 0.
The dimension of the Cantor middle thirds set is
log 2
log 3
0.6309.
The dimension of a line is 1.
The dimension of the von Koch curve is
log 4
log 3
1.262.
The dimension of the Minkowski sausage is 1.5.
The dimension of the dragon curve is 2.
Many more on Wikipedia.
Logan Axon (Notre Dame) Random fractals March 29, 2010 21 / 36
Romanesco broccoli (image source: Wikipedia)
Logan Axon (Notre Dame) Random fractals March 29, 2010 22 / 36
The coast of Britain
In one of his early papers on fractals Mandelbrot addressed the question,
How long is the coast of Britain? This is a hard question in part because
you get dierent answers depending on how much detail you include.
Image source: Wikipedia
Logan Axon (Notre Dame) Random fractals March 29, 2010 23 / 36
The coast of Britain
How long is the coast of Britain?
Mandelbrots answer was that the coast of Britain is a fractal and so
asking for the length is the wrong question. Instead a better measurement
is the fractal dimension, which Richardson estimated to be 1.25.
The coast of Britain is not strictly self-similar: it varies randomly. It is
stochastically self-similar.
We can get the same kind of stochastic self-similarity by adding an
element of randomness to our constructions.
Logan Axon (Notre Dame) Random fractals March 29, 2010 24 / 36
The coast of Britain
How long is the coast of Britain?
Mandelbrots answer was that the coast of Britain is a fractal and so
asking for the length is the wrong question. Instead a better measurement
is the fractal dimension, which Richardson estimated to be 1.25.
The coast of Britain is not strictly self-similar: it varies randomly. It is
stochastically self-similar.
We can get the same kind of stochastic self-similarity by adding an
element of randomness to our constructions.
Logan Axon (Notre Dame) Random fractals March 29, 2010 24 / 36
A random von Koch curve
Add randomness to the construction of the von Koch curve by ipping a
coin to decide if each triangle we add should point up or down.
.
.
.
.
.
.
Logan Axon (Notre Dame) Random fractals March 29, 2010 25 / 36
Two random von Koch curves
Logan Axon (Notre Dame) Random fractals March 29, 2010 26 / 36
A random Cantor set
As we construct the Cantor set, ip a biased coin to decide whether or not
to include each interval (after starting with [0, 1]). Include the interval if
the ip gives heads. For example, if the probability of heads is
2
3
:
H, H
T, T, H, H
T, H, H, T
H, T, T, H
H, H, H, T
.
.
.
Logan Axon (Notre Dame) Random fractals March 29, 2010 27 / 36
A random Cantor set
Let R be the random Cantor set obtained from this construction.
Question
Its possible that R = . How likely is this?
We can calculate the exact probability that R = , P(R = ), using the
self-similarity of the construction. The result depends on the bias of the
coin. Let p be the probability that the coin is heads.
Logan Axon (Notre Dame) Random fractals March 29, 2010 28 / 36
Calculating P(R = )
There are 3 ways that R can be empty:
1
Neither [0,
1
3
] nor [
2
3
, 1] is included.
2
Exactly one of [0,
1
3
] or [
2
3
, 1] is included and R is eventually empty
below that interval.
3
Both of [0,
1
3
] and [
2
3
, 1] is included and R is eventually empty below
both intervals.
The probability that R is eventually empty below [0,
1
3
] given that [0,
1
3
]
was included in the construction is exactly P(R = ) by self-similarity.
The same holds for [
2
3
, 1].
Logan Axon (Notre Dame) Random fractals March 29, 2010 29 / 36
Calculating P(R = )
The 3 ways that R can be empty:
1
Neither [0,
1
3
] nor [
2
3
, 1] is included.
2
Exactly one of [0,
1
3
] or [
2
3
, 1] is included and R is eventually empty
below that interval.
3
Both of [0,
1
3
] and [
2
3
, 1] is included and R is eventually empty below
both intervals.
Let q = P(R = ). Recall that p is the probability of heads. These events
happen with probabilities:
1
(1 p)
2
;
2
2p(1 p)q;
3
p
2
q
2
.
Logan Axon (Notre Dame) Random fractals March 29, 2010 30 / 36
Calculating P(R = )
Therefore q = P(R = ) is a solution to the equation
x = p
2
x
2
+ 2p(1 p)x + (1 p)
2
.
The solutions to this equation are 1 and
_
1p
p
_
2
. Which solution is
P(R = )?
If p
1
2
, then
_
1p
p
_
2
1. Hence
P(R = ) = 1.
On the other hand, P(R = ) 0 as p 1. Hence for p >
1
2
P(R = ) =
_
1 p
p
_
2
< 1.
Logan Axon (Notre Dame) Random fractals March 29, 2010 31 / 36
Calculating P(R = )
Therefore q = P(R = ) is a solution to the equation
x = p
2
x
2
+ 2p(1 p)x + (1 p)
2
.
The solutions to this equation are 1 and
_
1p
p
_
2
. Which solution is
P(R = )?
If p
1
2
, then
_
1p
p
_
2
1. Hence
P(R = ) = 1.
On the other hand, P(R = ) 0 as p 1. Hence for p >
1
2
P(R = ) =
_
1 p
p
_
2
< 1.
Logan Axon (Notre Dame) Random fractals March 29, 2010 31 / 36
Calculating P(R = )
Therefore q = P(R = ) is a solution to the equation
x = p
2
x
2
+ 2p(1 p)x + (1 p)
2
.
The solutions to this equation are 1 and
_
1p
p
_
2
. Which solution is
P(R = )?
If p
1
2
, then
_
1p
p
_
2
1. Hence
P(R = ) = 1.
On the other hand, P(R = ) 0 as p 1. Hence for p >
1
2
P(R = ) =
_
1 p
p
_
2
< 1.
Logan Axon (Notre Dame) Random fractals March 29, 2010 31 / 36
The dimension of a random Cantor set
If the random Cantor set is , then theres no point in asking about its
dimension. A theorem (next slide) tells us that if the random Cantor set is
not , then with probability 1 its dimension is the solution d of
3
d
(2p(1 p)) + 3
d
(2)p
2
= 1.
3
d
(2p(1 p)) + 3
d
(2)p
2
= 1 2p(1 p) + 2p
2
= 3
d
2p = 3
d
d =
log(2p)
log 3
For p =
2
3
, d 0.2619.
For p = 1, d =
log 2
log 3
0.6309, as we calculated before.
Logan Axon (Notre Dame) Random fractals March 29, 2010 32 / 36
The dimension of a random Cantor set
If the random Cantor set is , then theres no point in asking about its
dimension. A theorem (next slide) tells us that if the random Cantor set is
not , then with probability 1 its dimension is the solution d of
3
d
(2p(1 p)) + 3
d
(2)p
2
= 1.
3
d
(2p(1 p)) + 3
d
(2)p
2
= 1 2p(1 p) + 2p
2
= 3
d
2p = 3
d
d =
log(2p)
log 3
For p =
2
3
, d 0.2619.
For p = 1, d =
log 2
log 3
0.6309, as we calculated before.
Logan Axon (Notre Dame) Random fractals March 29, 2010 32 / 36
The dimension of a random Cantor set
If the random Cantor set is , then theres no point in asking about its
dimension. A theorem (next slide) tells us that if the random Cantor set is
not , then with probability 1 its dimension is the solution d of
3
d
(2p(1 p)) + 3
d
(2)p
2
= 1.
3
d
(2p(1 p)) + 3
d
(2)p
2
= 1 2p(1 p) + 2p
2
= 3
d
2p = 3
d
d =
log(2p)
log 3
For p =
2
3
, d 0.2619.
For p = 1, d =
log 2
log 3
0.6309, as we calculated before.
Logan Axon (Notre Dame) Random fractals March 29, 2010 32 / 36
A random Cantor set
For our random Cantor set we think of the construction as replacing each
component with 2 stochastically similar components. Each replacement
piece was either a
1
3
-scaled copy or a 0-scaled copy (i.e. ).
Logan Axon (Notre Dame) Random fractals March 29, 2010 33 / 36
The theorem
Consider a random Cantor set in which each component of the
construction is replaced by 2 copies with random scaling s
1
and s
2
. Let N
be the (random) number of these copies that is non-empty.
Theorem (Falconer, Graf, Mauldin, Williams)
This random Cantor set has probability q of being empty, where q = x is
the smallest non-negative solution to the equation
P(N = 0) +P(N = 1)x +P(N = 2)x
2
= x.
Logan Axon (Notre Dame) Random fractals March 29, 2010 34 / 36
The theorem continued
N is the (random) number of the copies that is non-empty and s
1
, s
2
are
the (random) scaling of the copies.
Theorem (Falconer, Graf, Mauldin, Williams)
This random Cantor set has probability q of being empty, where q = x is
the smallest non-negative solution to the equation
P(N = 0) +P(N = 1)x +P(N = 2)x
2
= x.
If it is not , then with probability 1 the random Cantor set has dimension
d, where d = y is the solution of
E
_
s
y
1
+ s
y
2
_
= 1.
Logan Axon (Notre Dame) Random fractals March 29, 2010 35 / 36
References
Kenneth Falconer. Fractal Geometry. Wiley, 2003.
Benoit B. Mandelbrot. How long is the coast of Britain? Statistical
self-similarity and fractional dimension. Science: 156, 1967.
Benoit B. Mandelbrot.
http://www.math.yale.edu/
~
bbm3/index.html.
Logan Axon (Notre Dame) Random fractals March 29, 2010 36 / 36
You might also like
- Characteristics of Counter Example Loops in The Collatz ConjectureDocument38 pagesCharacteristics of Counter Example Loops in The Collatz ConjectureDimas Cabré i ChacónNo ratings yet
- Philippine Christian UniversityDocument59 pagesPhilippine Christian UniversityRenzNo ratings yet
- PHYS 6553 Fall 2016 Problem Set 1 SolutionDocument8 pagesPHYS 6553 Fall 2016 Problem Set 1 SolutionJason HuaNo ratings yet
- Compton Scattering: Niklaus H Afliger (Niklaus@lcc - CH) January 19, 2010Document24 pagesCompton Scattering: Niklaus H Afliger (Niklaus@lcc - CH) January 19, 2010Niklaus HaefligerNo ratings yet
- Cantor Set FunctionDocument15 pagesCantor Set FunctionRenato GaloisNo ratings yet
- Fractals and DimensionDocument29 pagesFractals and DimensionfdsafjklsdakdasjffdafdsafsdNo ratings yet
- Boyce/Diprima 10 Ed, CH 10.7: The Wave Equation: Vibrations of An Elastic StringDocument39 pagesBoyce/Diprima 10 Ed, CH 10.7: The Wave Equation: Vibrations of An Elastic StringphakphumNo ratings yet
- Week 5 ÁÖ° Áø ÜÆò°¡ 12ÇÐ Â Math AA HLDocument3 pagesWeek 5 ÁÖ° Áø ÜÆò°¡ 12ÇÐ Â Math AA HLKevinNo ratings yet
- The Collage Theorem and Its Applications: Faculty Advisor: Jane Mcdougall Soyeon Kang April 8, 2016Document18 pagesThe Collage Theorem and Its Applications: Faculty Advisor: Jane Mcdougall Soyeon Kang April 8, 2016ayan.av0010No ratings yet
- Newton Raphson Fractals:A Review: International Journal of Emerging Trends & Technology in Computer Science (IJETTCS)Document5 pagesNewton Raphson Fractals:A Review: International Journal of Emerging Trends & Technology in Computer Science (IJETTCS)International Journal of Application or Innovation in Engineering & ManagementNo ratings yet
- FractalsDocument29 pagesFractalsrajivrama75% (4)
- Density Center of MassDocument6 pagesDensity Center of MassMagdaPinzónNo ratings yet
- ChrisShaver CantorSetPaper4 PDFDocument19 pagesChrisShaver CantorSetPaper4 PDFKamilNo ratings yet
- Box Counting DimDocument18 pagesBox Counting DimJose FernandezNo ratings yet
- 09 AnalysisDocument6 pages09 Analysismirjana zegaracNo ratings yet
- Calculus Non-Routine Problems and SolutionsDocument51 pagesCalculus Non-Routine Problems and Solutionskaushik247No ratings yet
- Assignment 3 - 1920Document2 pagesAssignment 3 - 1920smithson JoeNo ratings yet
- EE101 L3 Center of MassDocument20 pagesEE101 L3 Center of MassYao SsengssNo ratings yet
- OSC Calc03 SASG 01 01Document12 pagesOSC Calc03 SASG 01 01AlperenNo ratings yet
- Christopher Shaver - An Exploration of The Cantor SetDocument19 pagesChristopher Shaver - An Exploration of The Cantor SetNine000No ratings yet
- Fractals HandoutDocument15 pagesFractals HandoutJanelle Ann BacoNo ratings yet
- Exam #1 Problem 1 (35 Points) Isotopic AbundanceDocument5 pagesExam #1 Problem 1 (35 Points) Isotopic Abundance*83*22*No ratings yet
- Interference & DiffractionDocument36 pagesInterference & DiffractionsalafismeNo ratings yet
- Romero BHDocument121 pagesRomero BHDiego1980bNo ratings yet
- Romero-Apunte Agujeros NegrosDocument121 pagesRomero-Apunte Agujeros NegrosHauVuNguyenDuyNo ratings yet
- M39 Knig9404 Ism C39 PDFDocument22 pagesM39 Knig9404 Ism C39 PDFnorma_jeannNo ratings yet
- As Lecture11Document2 pagesAs Lecture11mrtfkhangNo ratings yet
- MAT130.5 (MTM) Handout #8 - Area Between Two Curves, Spring 2020Document25 pagesMAT130.5 (MTM) Handout #8 - Area Between Two Curves, Spring 2020Tasnim Alam Piyash 1731712No ratings yet
- Unit 1 NotesDocument50 pagesUnit 1 NotesAbbas KhanNo ratings yet
- 4 055 S ShatterWineGlass StudentVersionDocument5 pages4 055 S ShatterWineGlass StudentVersionPedro DuvanNo ratings yet
- 1963 1999Document74 pages1963 1999Itsos SotirisNo ratings yet
- QSP Examples1Document8 pagesQSP Examples1Utilities CoNo ratings yet
- Chalenge Problems On IntegrationDocument6 pagesChalenge Problems On IntegrationRomerio Ribeiro da Silva0% (1)
- 2.1 Rates of Change and LimitsDocument23 pages2.1 Rates of Change and Limitsnomore891No ratings yet
- Silk DampingDocument2 pagesSilk DampingAlexandre SimmerlingNo ratings yet
- Chap14 PDFDocument61 pagesChap14 PDFKarn KumarNo ratings yet
- Chaos Lecture NotesDocument16 pagesChaos Lecture Notessl1uckyNo ratings yet
- Section 3 - Brownian MotionDocument33 pagesSection 3 - Brownian MotionSamuel EricksonNo ratings yet
- Caotic Mechanics MaximaDocument25 pagesCaotic Mechanics MaximaStefano MilaniNo ratings yet
- MCV 4U1 Exam Review 1Document52 pagesMCV 4U1 Exam Review 1Eduardo Yépez M.No ratings yet
- GEC 104 Lecture NotesDocument6 pagesGEC 104 Lecture NotesAngela BatallangNo ratings yet
- Chapter 3 - Discrete Radom Variables and Probability DistributionDocument70 pagesChapter 3 - Discrete Radom Variables and Probability DistributionTran Minh Nhut (K17 HCM)No ratings yet
- Solid Mechanics Study Material PDFDocument35 pagesSolid Mechanics Study Material PDFirinat101No ratings yet
- Center of Mass: Ofa Solid of RevolutionDocument24 pagesCenter of Mass: Ofa Solid of RevolutionWati KaNo ratings yet
- 11 Upper Bound Resonances Anosov FlowsDocument40 pages11 Upper Bound Resonances Anosov FlowsFrédéric FaureNo ratings yet
- Functional AnalysisDocument96 pagesFunctional AnalysistimcantangoNo ratings yet
- Plane Waves and Problems of Steady Vibrations in The Theory of Viscoelasticity For Kelvin-Voigt Materials With Double PorosityDocument18 pagesPlane Waves and Problems of Steady Vibrations in The Theory of Viscoelasticity For Kelvin-Voigt Materials With Double PorosityAndreea BucurNo ratings yet
- Matind I 11-12-Integration ApplicationDocument18 pagesMatind I 11-12-Integration ApplicationDhesyarmani P. RothschildiNo ratings yet
- Fractals: Cantor Set, Sierpinski Triangle, Koch Snowflake, Fractal DimensionDocument7 pagesFractals: Cantor Set, Sierpinski Triangle, Koch Snowflake, Fractal DimensionNine000No ratings yet
- Spring Break Take Home Problems - AP CalculusDocument2 pagesSpring Break Take Home Problems - AP CalculusteachopensourceNo ratings yet
- What Is The Definition of A Fractal?Document12 pagesWhat Is The Definition of A Fractal?Hilda HandayaniNo ratings yet
- Three-Dimensional Matching Is NP-HardDocument4 pagesThree-Dimensional Matching Is NP-HardRaul HernándezNo ratings yet
- Baum Welch HMMDocument24 pagesBaum Welch HMMtruongvinhlan19895148No ratings yet
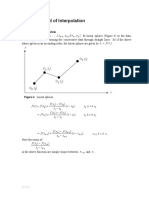
- Spline Method of InterpolationDocument7 pagesSpline Method of InterpolationNadineNo ratings yet
- AP Calculus BC Stuff You Must KnowDocument7 pagesAP Calculus BC Stuff You Must KnowJulian PradeepNo ratings yet
- C32 - Applications of Derivatives - Part 2Document22 pagesC32 - Applications of Derivatives - Part 2Triet TruongNo ratings yet
- Questions IE621Document10 pagesQuestions IE621KushNo ratings yet
- Chapter 2: Derivatives: by Assoc - Prof. Mai Duc ThanhDocument19 pagesChapter 2: Derivatives: by Assoc - Prof. Mai Duc ThanhTriet TruongNo ratings yet
- Trinity College Admissions Quiz (Mathematics With Physics 2) 1999Document3 pagesTrinity College Admissions Quiz (Mathematics With Physics 2) 1999oliverjohnboydNo ratings yet
- Structural Analysis Thesis PresentationDocument20 pagesStructural Analysis Thesis PresentationmifeNo ratings yet
- Vernacular Press ActDocument1 pageVernacular Press ActBabai KunduNo ratings yet
- Formation of Muslim LeagueDocument3 pagesFormation of Muslim LeagueBabai KunduNo ratings yet
- Warren HastingsDocument5 pagesWarren HastingsBabai Kundu100% (1)
- Indian National CongressDocument2 pagesIndian National CongressBabai KunduNo ratings yet
- Introduction of Railways and Telegraph SystemDocument2 pagesIntroduction of Railways and Telegraph SystemBabai KunduNo ratings yet
- Formation of Muslim LeagueDocument3 pagesFormation of Muslim LeagueBabai KunduNo ratings yet
- Gandhi Jinnah TalksDocument1 pageGandhi Jinnah TalksBabai KunduNo ratings yet
- Indian Flag: India's History: Modern India: History of Indian Flag - (1904 - 1947)Document3 pagesIndian Flag: India's History: Modern India: History of Indian Flag - (1904 - 1947)Babai KunduNo ratings yet
- Gandhi Irwin PactDocument2 pagesGandhi Irwin PactBabai KunduNo ratings yet
- First Partition of BengalDocument9 pagesFirst Partition of BengalBabai KunduNo ratings yet
- CorvusDocument25 pagesCorvusapi-3731524No ratings yet
- Bihar Earthquake: India's History: Modern India: Civil Disobedience Movement Called Off, Bihar Earthquake: 1934Document2 pagesBihar Earthquake: India's History: Modern India: Civil Disobedience Movement Called Off, Bihar Earthquake: 1934Babai KunduNo ratings yet
- First Anglo-Sikh WarDocument5 pagesFirst Anglo-Sikh WarBabai Kundu100% (2)
- Educational ResolutionDocument1 pageEducational ResolutionBabai KunduNo ratings yet
- Anglo Gurkha WarDocument1 pageAnglo Gurkha WarBabai KunduNo ratings yet
- Diwani RightsDocument2 pagesDiwani RightsBabai KunduNo ratings yet
- IPhO (1967 - 2010)Document1,279 pagesIPhO (1967 - 2010)Babai KunduNo ratings yet
- Feynman ParadoxDocument3 pagesFeynman ParadoxBabai KunduNo ratings yet
- Polynomial Time Reduction(s)Document8 pagesPolynomial Time Reduction(s)srinidhi paiNo ratings yet
- Cie Igcse o Level Maths Topic 4Document24 pagesCie Igcse o Level Maths Topic 4Nayeem HakimNo ratings yet
- Topic 5-20200317101441 PDFDocument15 pagesTopic 5-20200317101441 PDFHaffidzry HuzraynNo ratings yet
- Math Diagnostic TestDocument1 pageMath Diagnostic Testclaire de leonNo ratings yet
- Proceedings of The 15th International Conference of The International Association For Computer Methods and Advances in GeomechanicsDocument8 pagesProceedings of The 15th International Conference of The International Association For Computer Methods and Advances in GeomechanicsmkholmyNo ratings yet
- Centre No. Candidate No.Document28 pagesCentre No. Candidate No.rondonramlalNo ratings yet
- Algebra II SyllabusDocument3 pagesAlgebra II Syllabusapi-259543534No ratings yet
- A Note On Z-Algebra PDFDocument8 pagesA Note On Z-Algebra PDFPandu DoradlaNo ratings yet
- My Name IsDocument75 pagesMy Name IsKriez NamuhujaNo ratings yet
- Tws 4 CompleteDocument2 pagesTws 4 Completeapi-213553729No ratings yet
- 2x +X +x+5 (X +1) (X 2) : Ee 412 (Electrical Engineering Correlation 1) Mathematics SubjectsDocument4 pages2x +X +x+5 (X +1) (X 2) : Ee 412 (Electrical Engineering Correlation 1) Mathematics SubjectsgregNo ratings yet
- Solomon - Negative NRG in QEDDocument9 pagesSolomon - Negative NRG in QEDHomers SimpsonNo ratings yet
- Tabu Search Heuristics For The Vehicle Routing ProblemDocument2 pagesTabu Search Heuristics For The Vehicle Routing ProblemAndika Dwi NugrahaNo ratings yet
- Discrete - Time System and AnalysisDocument113 pagesDiscrete - Time System and Analysisapaijas0% (2)
- CMC 2009 PDFDocument25 pagesCMC 2009 PDFElevenPlus ParentsNo ratings yet
- Unit 3 Review LogarithmsDocument15 pagesUnit 3 Review LogarithmsdevikaNo ratings yet
- Lecture4 PDFDocument2 pagesLecture4 PDFjobel alejandrinoNo ratings yet
- HILL, Lester S. - Cryptography in An Algebraic AlphabetDocument8 pagesHILL, Lester S. - Cryptography in An Algebraic AlphabetDouglas DanielNo ratings yet
- Exercise EC5002 Econometrics All QuestionsDocument24 pagesExercise EC5002 Econometrics All Questionsnishit0157623637No ratings yet
- The Scalar Product: Engineering Application 7.6Document12 pagesThe Scalar Product: Engineering Application 7.6Pubg MobileNo ratings yet
- Prolog Programming Exercises1Document3 pagesProlog Programming Exercises1atmroo9No ratings yet
- Cot 1 2020-2021Document5 pagesCot 1 2020-2021Sinned NozidNo ratings yet
- Rotation MatriciesDocument6 pagesRotation MatriciesSoumya Civil SNo ratings yet
- Optimization Methods in Management Science: MIT 15.053, Spring 2013Document9 pagesOptimization Methods in Management Science: MIT 15.053, Spring 2013AnifaNo ratings yet
- Cbse 10Th Maths Exam 2020: Important Mcqs From Chapter 5 Arithmetic Progression With Detailed SolutionsDocument8 pagesCbse 10Th Maths Exam 2020: Important Mcqs From Chapter 5 Arithmetic Progression With Detailed Solutionszakir abbasNo ratings yet
- Math 10 - Q3 M3Document12 pagesMath 10 - Q3 M3Dizzi Dzen MendozaNo ratings yet
- Discriminant AnalysisDocument6 pagesDiscriminant AnalysisKARTHIKEYAN P 1727716No ratings yet
- Ut 01Document116 pagesUt 01obitobiuchiha15No ratings yet
- Reka Bentuk, Pembinaan Dan Pentadbiran UjianDocument9 pagesReka Bentuk, Pembinaan Dan Pentadbiran UjianAiman HazimNo ratings yet