Un'Introduzione Alla Teoria Quantistica Dei Campi

UnIntroduzione alla Teoria Quantistica dei
Campi
Paolo Guiotto
Contents
1 Introduzione 2
2 Il formalismo della Meccanica Hamiltoniana 2
2.1 Il principio di minima azione . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2 Il usso nello spazio delle fasi . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.3 Formulazione algebrica: parentesi di Poisson . . . . . . . . . . . . . . . . . . . 5
2.4 Teorema di Liouville ed unitarietà . . . . . . . . . . . . . . . . . . . . . . . . 6
3 La Meccanica Quantistica e la teoria degli operatori 8
3.1 Alcuni fatti sperimentali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.2 Il concetto di stato quantistico . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.3 Osservabili . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.4 Parentesi di Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.5 Il principio dindeterminazione . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.6 Quantizzazione delle osservabili fondamentali . . . . . . . . . . . . . . . . . . 16
3.6.1 Quantizzazione di Q . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.6.2 Quantizzazione di P . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3.6.3 Quantizzazione di H . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
3.7 Equazione di Schrodinger . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
3.8 LOscillatore Armonico . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.8.1 Analisi spettrale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.8.2 La formula di Mehler . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.9 Latomo di idrogeno . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4 La Formula di Feynman 35
4.1 LIntegrale Funzionale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.1.1 Il problema del rigore della formula di Feynman . . . . . . . . . . . . 39
4.2 La Formula di FeynmanKac . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.3 La misura di Wiener . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
4.4 Applicazioni della formula di FeynmanKac alla MQ . . . . . . . . . . . . . . 44
4.4.1 La legge di Planck . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
5 Il problema della QFT 45
5.1 Equazione di KleinGordon . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
5.2 Parentesi di Poisson . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48
5.3 Rappresentazione di Schrodinger . . . . . . . . . . . . . . . . . . . . . . . . . 50
5.3.1 Spazio degli stati: misure gaussiane in dimensione innita . . . . . . . 50
5.3.2 Regole di commutazione . . . . . . . . . . . . . . . . . . . . . . . . . . 52
5.3.3 Operatori di moltiplicazione e derivazione . . . . . . . . . . . . . . . . 53
1
2
5.3.4 Quantizzazione di H: rinormalizzazione . . . . . . . . . . . . . . . . . 55
1 Introduzione
La teoria quantistica dei campi (nel seguito QFT, dallinglese Quantum Field Theory) si propone
di descrivere la sica dei fenomeni che si svolgono su scala atomica, tenendo conto della teo-
ria geometrica dello spaziotempo introdotta dalla relatività generale. In parole povere si tratta
dellunicazione della meccanica quantistica (in seguito QM, Quantum Mechanics) con la meccanica
relativistica. A rigore quindi, per poter comprendere gli scopi e le tecniche della QFT bisognerebbe
conoscere a fondo scopi e tecniche delle due teorie dalla cui unicazione essa nasce. Essendo questa
unintroduzione alla QFT rivolta a studenti del secondo anno, i quali non hanno in genere una
conoscenza preliminare della QM e della relatività (ne generale, ne speciale), si dovrà ricorrere a
diversi compromessi. Di fatto la teoria della relatività non verrà nemmeno toccata.
Lobiettivo principale che ci proponiamo è quello di presentare un linguaggio matematico che
mostri il pi` u possibile lunitarietà formale della Meccanica Classica, Meccanica Quantistica e Teoria
Quantistica dei Campi, da un lato, dallaltro ci introduca ad alcuni strumenti matematici creati
appositamente per la descrizione e studio dei problemi connessi. Tali strumenti sono in genere
molto complessi ed uno studio sistematico occupa diversi capitoli dellAnalisi Funzionale, per cui
è impossibile sia mantenere un livello di generalità che di precisione formale. Non essendo questo
però lo scopo questa perdità sarà, speriamo, secondaria.
Essendo unambito importantissimo della sica teorica, la bibliograa relativa alla QFT è molto
consistente ma anche molto tecnica. Infatti, lapparato matematico richiesto è quello pi` u avanzato
creato dallanalisi funzionale nel corso del ventesimo secolo. Non è semplice, ne del resto è questo
lo scopo, tracciare una bibliograa essenziale sullargomento. Alcuni riferimenti, tuttavia, sia per
lessere divenuti pietre miliari che per essere abbordabili agli studenti del secondo anno, possono
essere facilmente dati:
Landau, Meccanica, Editori Riuniti
Arnold, Metodi Matematici della Meccanica Classica, Editori Riuniti
Dirac, I Principi della Meccanica Quantistica, Boringhieri
Von Neumann, Mathematical Foundations of Quantum Mechanics
Feynman, Quantum Mechanics and Path Integral, McGraw Hill
Un libro che ha un taglio da sica teorica sulla QFT è quello di Itzykson & Zuber, Quantum Field
Theory, Mc GrawHill. Un taglio pi` u matematico lo si trova nel libro di Glimm & Jae, Quantum
Physics, Springer. Un bellissimo libro (o meglio sarebbe collana) è quello di Reed & Simon, Modern
Methods of Mathematical Physics, Academic Press, specie il vol. 1 Functional Analysis e,
sopratutto, il vol. 2 Fourier Analysis, Self Adjointness, nel quale la teoria del campo libero
(ved. sez. 5) è presentata rigorosamente. Questi riferimenti, ad ogni modo, sono molto dicili
tecnicamente e non sono certo consigliabili come prima lettura.
Inne, va consigliato il meraviglioso libro di Feynman QED, Adelphi (in italiano) che, con un
linguaggio molto semplice, descrive tutta una serie di fenomeni caratteristici della sica atomica
che hanno spinto a costruire la QM e la QFT.
2 Il formalismo della Meccanica Hamiltoniana
Partiamo dal punto dinizio della sica classica, cioè dalle equazioni di Newton. Nel seguito con-
sidereremo sempre il caso in cui una sola particella è presente e questa si muove in uno spazio
sico unidimensionale, di modo da alleggerire le notazioni evitando i vettori (del resto la dierenza
è di secondaria importanza qui). Lo scopo di questa prima parte è di introdurre un formalismo
descrittivo della meccanica classica che verrà ripreso e adattato nella QM e nella QFT.
Come noto, la posizione q(t) al tempo t è descritta attraverso lequazione di Newton
m q(t) = qV (q(t)),
3
ove V (q) è lenergia potenziale. Introduciamo ora le equazioni di Hamilton. Posto p = m q, quantità
di moto (od in breve momento) lequazione di Newton è ricondotta ad un sistema di equazioni del
primo ordine:
_
_
_
q =
1
m
p,
p = qV,
(2.1)
ovvero, introducendo lenergia totale
H(q, p) =
1
2m
p
2
+V (q) = en. cinetica + en. potenziale
al sistema
_
q = pH,
p = qH.
(2.2)
I sistemi della forma generale (2.2) prendono il nome di sistemi hamiltoniani e lo studio delle loro
proprietà analitiche e geometriche ha dato importanti risultati alla meccanica classica.
2.1 Il principio di minima azione
`
E possibile caratterizzare le traiettorie di moto come quelle che minimizzano certi funzionali delle
traiettorie, funzionali che hanno una propria interpretazione sica. Introduciamo la quantità
/(q) =
_
t
1
t
0
1
2
q(t)
2
V (q(t))dt,
detta azione. Fissiamo la posizione iniziale q(t0) = q0 e quella nale q(t1) = q1. Il bel teorema che
segue descrive la meccanica classica:
Teorema 2.1 (Principio di minima azione) La traiettoria seguita dal sistema soluzione delle
equazioni (2.1) è quella che rende stazionaria lazione /.
Dim. Vediamo qualè la proprietà caratteristica di una traiettoria q che sia punto stazionario per
lazione. Se q è una generica traiettoria con la stessa posizione iniziale e nale di q, cioè q(t0) = q(t0),
q(t1) = q(t1), ed indichiamo con q = q q allora avremo che
/( q +q) /( q) = q/( q)q +o(q).
Un punto stazionario deve essere tale che la variazione di / per una piccola perturbazione della
traiettoria q sia trascurabile rispetto a . Ciò signica che si deve avere
q/( q) = 0.
Calcoliamo allora la variazione dellazione e verichiamo che questo fatto:
/( q +q) =
_
t
1
t
0
1
2
(
q(t) +

q(t))
2
V ( q(t) +q(t))dt
=
_
t
1
t
0
1
2
(
q(t)
2
+

q(t)
2
+ 2
q(t)

q(t)) V ( q(t)) qV ( q(t))q(t)dt +o(q)
= /( q) +
_
t
1
t
0
q(t)

q(t) qV ( q(t))q(t)dt +o(q)
int. per parti = /( q)
_
t
1
t
0
_
q(t) +qV ( q(t))

_
q(t)dt +o(q).
4
Dunque / = o(q) se e solo se
_
t
1
t
0
q(t) +qV ( q(t))q(t)dt = 0,

per ogni incremento q(t) tale che q(t0) = q(t1) = 0. Da questa arbitrarietà segue che
q(t) +qV ( q(t)) = 0, t [t0, t1].

Possiamo pertanto porre
q/(q) = q() +qV (q()),
notando che ad ogni q la derivata dellazione associa tutta una funzione. La versione hamiltoniana
del teorema è altrettanto semplice da provare. A tal ne introduciamo lazione hamiltoniana
S(q, p) :=
_
t
1
t
0
( q(t)p(t) H(q(t), p(t)))dt.
Teorema 2.2 La traiettoria nello spazio delle fasi seguita dal sistema soluzione delle equazioni
(2.2) è quella che rende stazionaria lazione hamiltoniana S.
Non ci occuperemo oltre dei principi variazionali. Ci ritorneremo solo verso la ne quando la formula
di Feynman e le sue generalizzazioni avranno reintrodotto fondamentalmente lazione.
2.2 Il usso nello spazio delle fasi
Se al sistema (2.2) aggiungiamo le condizioni iniziali q0 e p0, attraverso la soluzione è denito un
usso nello spazio delle fasi (cioè lo spazio delle q e delle p)
Tt(q0, p0) = (q(t, q0, p0), p(t, qo, po)).
Qui assumeremo che valgano buone ipotesi per garantire esistenza ed unicità globale alle soluzioni
del sistema (2.2) qualunque sia (q0, p0) R
2
. La teoria delle equazioni dierenziali garantisce che
Tt : R
2
R
2
è un dieomorsmo e che vale la legge di gruppo, cioè:
Tt+s = Tt Ts = Ts Tt.
Inoltre ovviamente T0 = Id. Queste proprietà caratterizzano i gruppi ad un parametro di dieomor-
smi. Inoltre, la scrittura (2.2) permette di derivare immediatamente il principio di conservazione
dellenergia:
d
dt
H(q(t), p(t)) = qH q +pH p
per (2.2)
= 0.
Un teorema pi` u profondo è il
Teorema 2.3 (Liouville)
1
[Tt[ = [[.
Dim. Dal cambiamento di variabili segue che
[Tt[ =
_
Tt
dqdp =
_
[det J(Tt)(q, p)[dqdp = [[,

purche [det J(Tt)(q, p)[ = 1. Questo è vero per t = 0 (T0 = Id). Basta poi provare che
d
dt
det J(Tt)(q, p) = 0,
1
Se R
2
è un aperto, [[ sta per la misura di .
5
e questo segue dal calcolo esplicito e dalla forma del sistema (2.2). Infatti: posto che Tt(q, p) =
(q(t, q, p), p(t, q, p)) (q, p) abbiamo che
J(Tt) =
_
qq pq
qp pp
_
, = det(J(Tt)) = qqpp pqqp.
Allora
d
dt
detJ(Tt) = (qqpp pqqp)
= q qpp +qqp p p qqp pqq p.

Derivando le equazioni di Hamilton si ottiene
q q = qpHqq +ppHqp,
p q = qpHpq +ppHpp,
q p = (qqHqq +qpHqp) ,
p p = (qqHpq +qpHpp) ,
e mettendo tutto assieme con un po di pazienza si vede subito che
d
dt
detJ(Tt) = 0.
Da questo segue che detJ(Tt) = detJ(T0) = 1, da cui la conclusione.
2.3 Formulazione algebrica: parentesi di Poisson
Introduciamo ora limportante concetto di osservabile. Matematicamente si tratta di una qualsiasi
(pi` u o meno) funzione sullo spazio delle fasi, cioè di una f : R
2
R. Se lo stato è caratterizzato
dalle coordinate (q, p), losservabile f vale f(q, p). Particolari osservabili sono le coordinate stesse,
Q(q, p) = q, P(q, p) = p.
Se f è un osservabile e consideriamo levoluzione del sistema il valore dellosservabile cambierà nel
tempo secondo la formula f(q(t), p(t)). Precisamente, se (q0, p0) è lo stato iniziale, f è losservabile,
al tempo t il valore dellosservabile sullo stato del sistema è:
f(q(t, q0, p0), p(t, q0, p0)) =: Ttf(q0, p0).
La scrittura di destra è la denizione che corrisponde al cosidetto punto di vista di Heisenberg
della meccanica. Signica che invece di pensare la dinamica sulle particelle (equazioni di Hamilton
(2.2)) si può immaginare che il sistema resti fermo e che invece siano le osservabili a muoversi.
Questa dinamica delle osservabili presenta una dierenza fondamentale con quella introdotta dalle
equazioni (2.2): mentre quella è in genere non lineare questa è lineare (in parole povere, pi` u semplice);
ovviamente il prezzo da pagare è che la dinamica delle osservabili è nello spazio delle osservabili che,
come spazio di funzioni è uno spazio innito dimensionale. Vediamo allora le equazioni di evoluzione
per le osservabili:
(Ttf)
=
d
dt
f(q(t), p(t)) = (qf) q + (pf) p = (qf)(pH) (pf)(qH) =: |f, Ht = Tt|f, H
(2.3)
dove
|f, g = (qf)(pg) (pf)(qg), (2.4)
si dicono parentesi di Poisson di f e g. Lordine è eettivamente importante poichè si vede imme-
diatamente che
|f, g = |g, f. (2.5)
6
Interessante è il calcolo delle parentesi di Poisson di Q e P:
|Q, P = (qQ)(pP) (pQ)(qP) = 1.
Le parentesi di Poisson (2.4) hanno altre notevoli proprietà. Anzitutto sono lineari in ciascun
argomento, nel senso che:
|c1f1 +c2f2, g = c1|f1, g +c2|f2, g, |f, c1g1 +c2g2 = c1|f, g1 +c2|f, g2. (2.6)
Poi si comportano come una derivazione
2
, nel senso che vale la regola del prodotto:
|fg, h = |f, hg +f|g, h. (2.7)
Meno evidente è la cosidetta identità di Lie:
|f, |g, h +||f, g, h +||f, h, g = 0. (2.8)
Lequazione (2.3) non si presenta in forma chiusa per la funzione f(t, q, p) := Ttf(q, p) a causa del
secondo membro. Tuttavia è semplice mostrare che eettivamente può essere scritta come
(Ttf)
= |Ttf, H (2.9)
Infatti:
(Ttf)
= lim
h0
T
t+h
f Ttf
h
= lim
h0
T
h
(Ttf) Ttf
h
= T0 |Ttf, H = |Ttf, H.
Il formalismo appena introdotto permette di descrivere appieno la meccanica classica:
Teorema 2.4 (Rappresentazione di Heisenberg) Sia H una funzione hamiltoniana, |, le
parentesi di Poisson, Q e P le osservabilicoordinate. La meccanica classica è descritta dalle seguenti
due proprietà:
i) ogni osservabile ft f(t, q, p) soddisfa lequazione di Heisemberg
ft = |ft, H,
ii) |Q, P = 1.
Lo spazio delle osservabili con le parentesi di Poisson di chiama algebra di Lie.
La precedente formulazione è naturale ed importante. Infatti la meccanica quantistica verrà in-
trodotta sullo stesso schema formale (ciò che cambierà radicalmente sarà lalgebra di Lie delle
osservabili, cambiamento obbligato dai risultati sperimentali).
2.4 Teorema di Liouville ed unitarietà
Per apprezzare bene il formalismo di Heisenberg vediamo come da esso sia possibile ritrovare il
teorema di Liouville 2.3, in termini di proprietà algebricogeometriche che derivano dal teorema
2.4. A tal proposito andiamo a studiare meglio loperatore /Hf := |f, H. /H è unoperatore
lineare e lequazione di Heisenberg diventa
ft = /Hft,
dove

rappresenta la derivata rispetto a t. Ora, per analogia con le equazioni dierenziali ordinarie,
potremmo scrivere
ft = e
t1
H
f0.
La notazione e
t1
H
è per ora puramente ttizia ma suggestiva, e sta semplicemente per loperatore
Tt introdotto nella sezione precedente. Siccome parliamo di operatori è bene dire qualcosa su cosa
operano, cioè sulle famose osservabili.
`
E conveniente pensare lo spazio innito dimensionale delle
2
Niente di strano del resto: f, g è denita nella (2.4) attraverso derivate!
7
osservabili come una struttura di spazio vettoriale munito di unapposita topologia. Uno degli spazi
migliori (perche ricco di struttura) è lo spazio
H := L
2
(R
2
) =
_
f : R
2
C :
_
R
2
[f(q, p)[
2
dqdp < +
_
.
La ricchezza di tale spazio è non solo nella struttura vettoriale, ma anche nel fatto che H è munito
di un prodotto scalare hermitiano:
(f, g)
H
:=
_
R
2
f(q, p)g(q, p) dqdp
_
R
2
fg dqdp.
In questo caso
_
R
2
[f[
2
dqdp = (f, f)
2
H
è una norma come si verica facilmente e lo spazio H è
topologicamente completo (e prende il nome di spazio di Hilbert). Osserviamo che tale scelta di H ci
fa subito escludere le nostre osservabili importanti Q, P, H, ma questo è un problema cui bisognerà
abituarsi e che emergerà in tutta la sua complessità con la meccanica quantistica.
Chiaramente e
t1
H
f = Ttf è denita per ogni tipo di osservabile, quindi anche per una f H.
Meno evidente è che stia ancora in H. Assai meno evidente è che la dinamica non ne muti la
lunghezza in H. Questo è di fatto il teorema di Liouville:
Teorema 2.5
Teorema di Liouville e
t1
H
è unitario su H, t R.
Unitario signica che
_
_
e
t1
H
f
_
_
H
= |f|
H
, f H, t R.
Dim. Infatti basta osservare che
[[ =
_
1 dqdp =
_
R
2
[[
2
dqdp = ||
2
H
,
e
[Tt[ =
_
Tt
1 dqdp =
_
R
2
[Tt[
2
dqdp
=
_
R
2
[ Tt[
2
dqdp =
_
R
2
e
t1
H
2
dqdp
=
_
_
e
t1
H
_
_
2
H
.
Dunque se e
t1
H
è unitario su H per ogni t R chiaramente vale Liouville. Viceversa, se vale
Liouville abbiamo che e
t1
H
è unitario sulle funzioni caratteristiche. Basta allora procedere per
approssimazione attraverso funzioni semplici
c
k
k
,
k
disgiunti e si prova rapidamente il caso
generale.
`
E importante slegare lunitarietà dalla dinamica per poter estendere il teorema di Liouville ad altri
ambiti. Proviamo a vedere se cè una proprietà caratteristica intrinseca che si lega allunitarietà.
Se e
t1
H
fosse un numero complesso, lunitarietà signicherebbe che e
t1
H
= e
i
dove R,
ovvero che /H è, in qualche senso, un immaginario puro. Se /H fosse un vero e proprio numero
complesso, il fatto che sia immaginario puro sarebbe espresso dallidentità:
/H = /H.
Ma cosè il coniugato di /H? Attraverso il prodotto hermitiano è possibile darne una caratteriz-
zazione:
(/Hf, g)
H
= (f, /Hg)
H
= (f, /Hg)
H
.
8
Prima di proseguire diciamo qualche parola su /H. Perche se e
t1
H
, conoscendo la dinamica, non ha
grossi problemi di denizione, /H ne ha.
`
E infatti unoperatore dierenziale quindi è richiesta una
restrizione sulle osservabili per poter parlare di /Hf. Verrebbe naturale considerare, per esempio,
come dominio di /H le osservabili f C
1
(R
2
)H. Ciò è insuciente però perche in genere /Hf non
apparterrà ad H. Per stare tranquilli facciamo una restrizione pesante e prendiamo in considerazione
solo osservabili che siano C
(R
2
) a supporto compatto: scriveremo C
c
per indicare tale spazio.
`
E
adesso possibile mostrare il
Lemma 2.6 /H è antisimmetrico, ovvero
(/Hf, g)
H
= (f, /Hg)
H
, f, g C
c
.
Dim. Si tratta della formula dintegrazione per parti:
(/Hf, g)
H
=
_
R
(/Hf) g dqdp
=
_
R
(qf)(pH) g dqdp
_
R
(pf)(qH) g dqdp
=
_
R
fq (pH g) dqdp +
_
R
fp (qH g) dqdp
=
_
R
f (qpH g +pHq g) dqdp +
_
R
f (pqH g +qHp g) dqdp
=
_
R
f(pHqg qHpg)dqdp.
= (f, /Hg)
H
.
Lunitarietà segue direttamente dallantisimmetria in modo formale (indipendente cioè dalla speci-
ca forma di /H):
Corollario 2.7 Se /H è antisimmetrico allora e
t1
H
è unitario su H.
Dim. Poniamo ut := e
t1
H
f, formiamo la quantità |ut|
2
H
e deriviamo rispetto a t tenendo conto
che
ut = /Hut.
Dunque
d
dt
|ut|
2
H
=
d
dt
(ut, ut)
H
= (ut, ut)
H
+ ( ut, ut)
H
= (ut, /Hut)
H
+ (/Hut, ut)
H
= 0.
3 La Meccanica Quantistica e la teoria degli operatori
La meccanica quantistica è nata dalla necessità di una nuova teoria per lo studio dei misterio-
si fenomeni
3
che si vericano su scala atomica. Di fatto lapparato matematico coinvolto nella
3
Rispetto alle concezioni classiche.
9
costruzione della teoria comprende fondamentali capitoli della matematica del ventesimo secolo,
capitoli nati proprio per fornire una solida base alle paradossali regole della teoria sica. Queste
teorie sono la teoria spettrale di operatori, la teoria delle algebre di Banach, la teoria della misura
su spazi di dimensione innita. Il successo spettacolare qualitativo e quantitativo di queste tecniche
nella spiegazione dei nuovi fenomeni ha dichiarato indiscussamente la correttezza della QM. Per
cominciare allora andiamo brevemente a riprodurre lesperimento virtuale cos` come Feynman lo
riporta nel suo libro Quantum Mechanics and Path Integral (è consigliabile anche il libretto
QED di Feynman).
3.1 Alcuni fatti sperimentali
Lesperimento virtuale
4
che ora descriveremo metterà in luce le caratteristiche misteriose della
sica atomica. Una sorgente di elettroni emette elettroni indistintamente in tutte le direzioni del
piano (immaginiamo per semplicità una dinamica unidimensionale, cioè in una sola dimensione
spaziale). Ad una certa distanza cè una paratia con due fori attraverso i quali gli elettroni possono
passare per andare poi a sbattere contro uno schermo. Lo schermo è munito di rilevatori sensibili a
sucienza da segnalare larrivo del signolo elettrone sullo schermo.
Supponiamo di far emettere alla sorgente un gran numero di elettroni in ciascuno dei tre seguenti
casi: a) il solo foro A è aperto; b) il solo foro B è aperto; c) tutti e due i fori sono aperti. La prima
sorpresa si coglie già con gli esperimenti a) e b) poichè quello che vediamo è che, a fronte di un
gran numero di prove gli elettroni sembrano distribuirsi casualmente sullo schermo, con un picco
pi` u o meno smorzato, allaltezza del foro corrispondente.
Quando i due fori sono aperti contemporaneamente succede qualcosa di nuovo. Non si ha una
semplice sovrapposizione dei due casi in cui uno solo dei fori è aperto: la frequenza di arrivare sullo
schermo passando per uno dei due fori non è la somma delle frequenze di passaggio attraverso uno
dei due fori. In parole povere la frequenza non soddisfa le leggi ordinarie del calcolo delle probabilità.
Diverse e complicate spiegazioni sono state date di questo fenomeno. Latteggiamento pragmatico
di prendere atto della situazione e cercare di trovare le nuove regole di calcolo è quello che ha
prodotto i migliori frutti, giacchè è chiaro che le regole della meccanica newtoniana non saranno
pi` u sucienti.
Prima di cedere al pragmatismo possiamo eettuare la seguente variante dellesperimento virtuale.
Subito dietro la paratia, in prossimità di uno dei due fori, quello A ad esempio, mettiamo un
rilevatore di particelle di modo tale che esso scatti quando una particella attraversa il foro A. Lo
scopo è quello di contare esattamente quante particelle passano per A (e di conseguenza quante
passano per B). Se questo apparecchio di rilevazione non inuenzasse il sistema ci aspetteremmo,
dopo lemissione di un gran numero di elettroni, la situazione misteriosa di cui abbiamo appena
detto. Ed invece, non senza stupore, ecco che ciò che si verica sullo schermo nale è proprio lesito
che ci aspetteremmo secondo le leggi classiche del calcolo delle probabilità!
Spiegare questo ulteriore mistero è stato un gran rompicapo per diverso tempo, ntanto che
Heisenberg formulò lipotesi che lapparecchio dovesse inuenzare lesito dellesperimento. Infatti,
egli disse, per constatare il passaggio di unelettrone dobbiamo in qualche modo toccarlo, e ciò è
possibile solo attraverso un urto con unaltra particella di massa pi` u o meno simile (o pi` u grande),
che nellurto nirà con linuenzare il moto dellelettrone.
`
E un po come se lelettrone è un passante
che vuole attraversare la strada e lunico modo di sapere se sta attraversando è quello di andargli
addosso con unautotreno!
Linuenza dellosservazione sullo stato del sistema ha unulteriore conseguenza logica (sperimen-
talmente vericata): in genere, se si compiono due osservazioni successive, lordine nel quale queste
avvengono avrà molta importanza e non è aatto detto che eettuare una prima misurazione di
una certa quantità e poi, successivamente, osservarne una seconda produca lo stesso eetto che
invertendo lordine delle osservazioni.
4
Virtuale perchè non concretamente realizzabile negli stessi termini che qui verranno esposti, ma
sostanzialmente realizzabile.
10
3.2 Il concetto di stato quantistico
Assumiamo allora latteggiamento pragmatico.
`
E anzitutto chiaro che il concetto di stato dovrà
subire un radicale cambiamento. In eetti laspetto aleatorio legato allimprevedibilità di dove si
possa trovare una particella costituisce una novità fondamentale in contrasto col determinismo delle
equazioni dierenziali di Newton. Precisamente non sarà pi` u possibile individuare una posizione
precisa ma solamente la probabilità che la particella si trovi in una certa posizione. Una prima idea
potrebbe essere quella di identicare lo stato con una distribuzione di probabilità, cioè con una
funzione : R [0, +[, tale che
_
+
(x) dx = 1. (3.1)
Dunque non avrà senso, in genere, calcolare la probabilità che la particella si trovi in un determinato
punto x quanto, invece,
P(particella [a, b]) =
_
b
a
(x) dx.
Tuttavia tale posizione non è suciente. Infatti il problema è adesso: negli esperimenti descritti
nella sezione precedente, nei tre casi a), b), c) dovremmo avere tre distribuzioni di probabilità 1,
2 e 3 che descrivono la probabilità nale di trovare una particella sullo schermo; come si legano
tra loro le tre distribuzioni? Se valessero le regole del calcolo delle probabilità ordinario, allora, per
la decomposizione delle probabilità totali,
P(particella [a, b]) = P(particella [a, b] [ passa per porta 1) P(passa per porta 1)
+ P(particella [a, b] [ passa per porta 2) P(passa per porta 2)
Ora: se le due porte sono identiche e sono simmetriche rispetto alla posizione in linea della sorgente
di elettroni, possiamo ammettere che P(passa per porta 1) = P(passa per porta 2) =
1
2
. Invece
P(particella [a, b] [ passa per porta 1) la possiamo calcolare tenendo conto che quando mettiamo
un rilevatore dopo una porta le di stribuzioni di probabilità nali coincidono con quelle di un solo
foro aperto. In altre parole
P(particella [a, b] [ passa per porta 1) =
_
b
a
1(x) dx,
P(particella [a, b] [ passa per porta 2) =
_
b
a
2(x) dx,
da cui, tenendo tutti e due i fori aperti, ammettendo la regola delle probabilità totali e le considerate
le osservazioni sperimentali, abbiamo che
1
2
_
b
a
1(x) dx +
1
2
_
b
a
2(x) dx =
_
b
a
1
2
(1(x) +2(x)) dx.
Conclusione: 3 =
1
2
(1 +2). Ebbene questa è falsa in virt` u dellaspetto della terza distribuzione!
Ma allora, qualè la misteriosa alchimia che permette di calcolare 3 in funzione 1 e 2?
Fortunatamente la situazione non era del tutto sconosciuta nella sica. Infatti ricordava la cosidetta
interferenza fra onde, che si ottiene quando si immagina che una perturbazione donda abbia origine
nel punto di emissione degli elettroni. Prendendo spunto da questa analogia dotiamo 1 e 2 anche
di una fase, ovvero pensiamo 1, 2 come funzioni complesse di variabile reale. Questo semplica
la struttura della prima regola, che ci permette di esprimere lo stato 3 come semplice combinazione
degli stati 1 e 2:
Assioma 3.1 (Principio di sovrapposizione)
3 = 1 +2.
11
Attraverso il principio di sovrapposizione possiamo guardare allo spazio degli stati come ad una
struttura di uno spazio vettoriale di funzioni da R in C. Naturalmente sarà opportuno fare una
specica pi` u precisa su tale spazio e scegliere da un lato uno spazio con una struttura conveniente
da un punto di vista algebricotopologico; dallaltro bisogna anche trovare il modo di estrarre il
senso probabilistico dalla conoscenza dello stato . Tali vincoli trovano unecace risposta nella
seguente scelta:
Assioma 3.2 (Spazio degli stati) Lo spazio degli stati è
X :=
_
: R C :
_
+
[(x)[
2
dx <
_
=: L
2
(R).
Tale spazio si assume munito della struttura di prodotto scalare hermitiano (, )
X
:=
_
R
f g dx.
Con tale posizione ||
2
X
= (, )
X
.
Chiaramente adesso X, in genere, non rappresenta pi` u una distribuzione di probabilità. La
strada per recuperare tale signicato probabilistico è quella di denire, per un dato stato X
_
b
a
[(x)[
2
dx.
Ovviamente tale posizione ha un senso probabilistico solo quando
_
R
[(x)[
2
dx = 1, ovvero ||
X
=
1.
Denizione 3.3 Uno stato X tale che ||
X
= 1 si dice unitario.
Osserviamo che per ogni stato ,= 0 si ha che := ||
1
X
è unitario. Per cui, se poniamo, in un
dato stato X
_
b
a
[(x)[
2
dx =
1
||
2
X
_
b
a
[(x)[
2
dx,
abbiamo una denizione valida per ogni stato ,= 0. Non solo: da questa denizione vediamo che,
ai ni di calcolo statistico, le probabilità sono invarianti sulle rette | : C.
3.3 Osservabili
Una volta introdotto il concetto di stato ed il principio di sovrapposizione che ci permette di
operare sugli stati, dobbiamo introdurre il secondo concetto fondamentale, quello di osservabile.
Come sempre unosservabile sarà una funzione dello stato. Il principio di sovrapposizione e quanto
detto nella sezione 3.2 impongono che sia un operatore lineare. Vediamo come.
Sia F unosservabile e uno stato; F() sarà la realizzazione di F in . Abbiamo detto, nel
paragrafo 3.2, che compiere unosservazione su un sistema in un certo stato corrisponde a cambiarne
lo stato in uno nuovo. In altre parole F : X X. Lidea che impone la restrizione agli operatori
lineari si basa sul principio che le relazioni siche siano conservate dalle osservabili. Per esempio:
se uno stato è sovrapposizione di altri due, cioè = 1 + 2 allora è naturale che, se F è
unosservabile, il trasformato di attraverso losservazione F sia la sovrapposizione dei trasformati
F(1) ed F(2)
5
. Cioè F() = F(1)+F(2). Allo stesso modo lo stato e c, dove c è un numero
complesso, rappresentano lo stesso stato; pertanto è naturale che F conservi questa relazione, cioè
F(c) e F() siano lo stesso stato a meno di una costante moltplicativa c. Per analogia con lalgebra
lineare è uso denotare lazione di unosservabile F su uno stato col simbolo F, a ricordare che
si tratta di un operatore lineare.
Assioma 3.4 (Osservabili) Si chiama osservabile ogni operatore lineare F : D(F) X X.
5
N.B. : questa è unipotesi ben precisa che trova conferme sperimentali nelle osservabili pi` u comuni.
12
Notiamo che il concetto di osservabile appena introdotto risponde bene anche al fatto che, in genere,
due osservabili F e G non commutino tra loro, cioè FG in genere è diverso da GF. Questo fatto
è vero non appena si prendono due operatori lineari su uno spazio vettoriale (si pensi ad esempio
al caso delle matrici in R
2
) e costituisce un principio di consistenza con ciò che stiamo andando a
costruire.
Ora che possediamo il concetto di spazio degli stati e di osservabile possiamo considerare una situ-
azione di grandissima importanza, è cioè linterpretazione dei concetti di autovalore ed autovettore.
Supponiamo che F sia unosservabile e che sia uno stato tale che
F = .
Ricordiamo che e rappresentano lo stesso stato, visto che lunica cosa che ci serve degli stati
è la probabilità di trovare la particella da qualche parte, operazione che si eettua come descritto
nel paragrafo precedente (normalizzando cioè, e quindi dimenticandosi della lunghezza eettiva del
vettore ). Un autostato per losservabile F è dunque uno stato su cui losservabile non inuisce
poichè riproduce lo stato stesso, a meno di un fattore intensivo. Possiamo interpretare questo
fattore come il valore eettivo dellosservabile
6
. Il valore può essere ottenuto attraverso la formula
(, ) = (, ) = (F, ),
ovvero
=
(F, )
(, )
.
Nel caso di unosservabile generica F e di uno stato che non sia autostato di F abbiamo la
Denizione 3.5 Si dice valore medio di unosservabile F nello stato il numero
F) :=
(F, )
(, )
, D(F).
Osserviamo che se è unitario allora F) = (F, ).
Si pone ora però un altro problema. In genere, per come è denito, F) non è detto che sia un
numero reale. Dipende dal fatto che (F, ) lo sia. Daltra parte le sole misurazioni che sicamente
hanno senso sono reali. Si potrebbe pensare di ottenere una misurazione complessa con due mis-
urazioni successive, di due quantità reali. Tuttavia, come abbiamo detto, una misura sul sistema
cambia lo stato delle cose ed inuirà sullesito della seconda misurazione. Daltro canto lordine è
fondamentale, quindi non si riesce a dare un senso ad una misurazione complessa. Vediamo anzitutto
cosa caratterizza lessere reale dei valori medi:
Lemma 3.6 F) R per ogni stato X se e solo se
(F, ) = (, F), , D(F).
In altre parole: se e solo se F è simmetrico.
Dim. Che se F è simmetrico allora i suoi valori medi sono reali è una semplice verica: se
D(F) è unitario allora
F) = (F, ) = (, F) = (F, ) = F).
Viceversa: sia D(F) unitario. La stessa relazione scritta sopra (assumendo che F) = F))
porta a
(F, ) = (F, ) = (, F),
6
Si potrebbe argomentare come segue. Losservabile F valutata su restituisce restituisce interamente
, ovverosia con certezza. Vedremo nella sezione 3.7 in che senso sintende con certezza.
13
per ogni D(F). Al caso generale si passa con tecniche standard di spazi di Hilbert (cioè
sostituendo con + e svolgendo i conti). Vediamo:
(F( +), +) = ( +, F( +)),
(F, ) + (F, ) + (F, ) + (F, ) = (, F) + (, F) + (, F) + (, F),
(F, ) + (F, ) = (, F) + (, F),
(F, ) (, F) = (, F) (F, ),
Ora: rimpiazziamo con i. Facendo i conti otteniamo
(F, i) (, iF) = (i, F) (iF, ),
i(F, ) +i(, F) = i(, F) i(F, ),
(F, ) (, F) = ((, F) (F, )) = ((F, ) (, F))
da cui, inne, (F, ) (, F) = 0.
Dunque gli operatori simmetrici rivestono un ruolo importante nella teoria, essendo corrispondenti
alle osservabili reali. Per unoperatore qualunque possiamo denire lanalogo del complesso coniugato
che verrà chiamato aggiunto: se F è loperatore, laggiunto di F, indicato con F
, sarà loperatore
soddisfacente lequazione
(F, ) = (, F
).
`
E facile provare, ad esempio, che (FG)
= G
e lordine è importante. Questo fra laltro mette

in luce che non è detto che il prodotto di due osservabili reali sia ancora unosservabile reale: questo
accade se e solo se F e G commutano.
3.4 Parentesi di Poisson
Seguendo la reppresentazione di Heisenberg dobbiamo ora introdurre le parentesi di Poisson. Infatti,
al momento, non disponiamo delle equazioni di Newton per conoscere levoluzione degli stati. Il
programma consiste allora nellintrodurre le nuove parentesi di Poisson quindi, attraverso lequazione
di Heisenberg, levoluzione delle osservabili ed inne dedurre levoluzione degli stati. Loperazione
di costruzione delle parentesi di Poisson quantistiche viene chiamata quantizzazione.
Indicheremo con [, ] le nuove parentesi quantistiche. Imponiamo che soddisno le proprietà (2.5),
(2.6), (2.7) e (2.8). Bisogna fare in realtà un po dattenzione con la (2.7). In eetti per le parentesi
di Poisson classiche è pur vero che tutti gli oggetti sono funzioni ed il prodotto è denito come
prodotto punto per punto, per cui è commutativo. In altre parole le quattro espressioni
|f, hg +f|g, h, g|f, h +f|g, h, g|f, h +|g, hf, |f, hg +|g, hf,
sono identiche. Se ora le osservabili sono operatori e le parentesi di Poisson di due osservabili è ancora
unosservabile in generale ci sarà da aspettarsi che le quattro espressioni di cui sopra, nel contesto
quantistico, siano tutte diverse. Come denire allora le parentesi? Bisogna ssare una convenzione
una volta per tutte. Tale convenzione è la cosidetta convenzione dellordine, che corrisponde alla
scelta della (2.7):
Assioma 3.7 (Parentesi quantistiche) Le parentesi [, ] soddisfano le seguenti condizioni:
i) (linearità) : [c1F1 +c2F2, G] = c1[F1, G] +c2[F2, G];
ii) (antisimmetria) : [F, G] = [G, F];
iii) (derivazione) : [FG, H] = [F, H]G+F[G, H];
iv) (identità di Lie) : [F, [G, H]] + [[F, G], H] + [[F, H], G] = 0;
14
v) (chiusura) : se F e G sono osservabili reali allora anche [F, G] lo è.
Ciò detto riusciamo a determinare la forma esplicita delle parentesi:
Teorema 3.8 (Dirac) Esiste una costante universale h R tale che
ih[F, G] = (FGGF).
La costante h si chiama costante di Planck.
Dim. Scriviamo la formula del prodotto [A, BC] applicando la ii) e la iii). Risulta:
[A, BC] = [BC, A] = ([B, A]C +B[C, A]) = [A, B]C +B[A, C]. (3.2)
Calcoliamo ora il prodotto [AB, CD] usando le due formule per il prodotto in cascata prima in un
ordine e poi in quello inverso.
[AB, CD] = [A, CD]B +A[B, CD]
= ([A, C]D +C[A, D]) B +A([B, C]D +C[B, D])
= [A, C]DB +AC[B, D] + C[A, D]B +A[B, C]D.
(3.3)
Allo stesso modo ma usando prima la regola (3.2) si perviene a
[AB, CD] = [A, C]BD +CA[B, D] + A[B, C]D +C[A, D]B.
Eguagliando con la (3.3) e cancellando le parti comuni si arriva a
[A, C](BD DB) = (AC CA)[B, D],
ovvero
(7)
(AC CA)
1
[A, C] = [B, D](BD DB)
1
.
Questo per ogni quaterna di operatori A, B, C, D. Poichè il primo membro non dipende da B, D ed
il secondo da A, C segue che devono essere costanti, nel senso che devono essere loperatore kI
per un opportuno k C indipendente da A, B, C, D, ovvero
[F, G] = k(FGGF).
Vediamo ora che k è immaginario puro. Se F e G sono osservabili reali la condizione che [F, G] lo
sia si legge come:
[F, G]
= [F, G]. (3.4)

Del resto
[F, G]
=

k(FGGF)
=

k(G
) =

k(GF FG) =
k(FGGF) =
k
k
[F, G].
Per cui la (3.4) può essere vera solo se
k =
k,
ovvero k è immaginario puro.
Le parentesi
ih[F, G] = (FGGF),
soddisfano lassioma 3.7 e dunque saranno il nostro punto di partenza per la costruzione delle
equazioni di evoluzione, oltre alla caretterizzazione delle funzioni Q e P (posizione ed impulso) che
dovranno soddisfare la relazione
[Q, P] = I. (3.5)
7
Sebbene un po sportivamente. . .
15
Vedremo tra poco come sia possibile costruire le versioni quantistiche delle funzioni Q, P che
soddisno la (3.5) e la versione quantistica dellhamiltoniana H. Notiamo ora il seguente particolare:
lequazione di commutazione (3.5) può essere esplicitamente riscritta come
QP PQ = ihI.
In meccanica classica è ben noto che le coordinate canoniche Q e P commutano. Ciò corrisponde al
valore h = 0. In eetti la costante h è molto piccola una volta rapportata alle situazioni concrete.
Possiamo in questo modo intravedere lo spiraglio che permette di riottenere la meccanica classica
da quella quantistica come caso limite quando la costante h tende a 0.
3.5 Il principio dindeterminazione
Mostriamo la potenza del linguaggio introdotto recuperando una delle pi` u sorprendenti conclusioni
della teoria: il principio dindeterminazione di Heisenberg.
A tal ne introduciamo un concetto nuovo. Abbiamo detto che se F è unosservabile allora il
suo valore medio nello stato è dato dal numero F) = (F, ) (se è unitario).
`
E importante
introdurre una quantità che misuri lo scostamento dal valore medio:
Denizione 3.9 (Varianza) Se F è unosservabile si pone
Var(F, ) := (F F)I)
2
) = ((F F)I)
2
, )
Due importanti fatti sono i seguenti:
i) Se F è unosservabile reale allora
Var(F, ) = ((F F)I)
2
, ) = ((F F)I), (F F)I)) = |(F F)I)|
2
.
ii) Se è un autostato per losservabile F, cioè F = , allora F) = , per cui
Var(F, ) =
(F F)I)
2
_
= ((F I)(F I), ) = 0,

ovvero Var(F, ) = 0.
Questo evidentemente corrisponde allinterpretazione che abbiamo dato agli autostati e cioè che su
di essi la misura della grandezza di cui sono autostati è determinata con certezza. Questa perfetta
descrizione mostra come le nuove regole di calcolo che stiamo introducendo siano coerenti con
linterpretazione cui esse corrispondono; questo è un punto fondamentale in tutta la sica teorica.
Consideriamo ora la relazione
QP PQ = ihI,
ammettendo di aver costruito Q e P come osservabili reali. Poniamo
Q :=
_
Var(Q, ) = |(QQ)I)|,
ed una simile denizione per P.
Teorema 3.10 (Principio dindeterminazione di Heisenberg)
QP
h
2
.
Osservazione 3.11 Detta in parole povere: il prodotto fra gli errori che si possono commettere
misurando Q e P simultaneamente è limitato inferiormente. Nella notazione di Heisenberg qp
h
2
, per cui se uno degli errori è piccolo laltro deve essere grosso.
16
Dim. Osserviamo che dallidentità
QP PQ = ih,
segue immediatamente la stessa con Q e P centrate rispetto al valore medio:
(QQ)I)(P P)I) (P P)I)(QQ)I) = ihI.
Per alleggerire la notazione indichiamo con Q := Q Q)I ed unanaloga denizione per P.
Dunque lequazione precedente si riscrive come
(Q)(P) (P)(Q) = ihI.
Ma allora, preso D(Q) D(P) unitario abbiamo
ih = i(, )
= ((QP PQ) , )
= (QP, ) (PQ, )
= (P, Q) (Q, P) Q, P simmetrici perche reali
= (P, Q) (P, Q)
= i2Im(P, Q) ,
da cui
h
2
[(P, Q)[
|P||Q| per CauchySchwarz
= QP.
3.6 Quantizzazione delle osservabili fondamentali
Fin qui abbiamo introdotto lo spazio degli stati e come sono fatte le osservabili. Tenendo conto
di ciò abbiamo derivato la forma delle parentesi di Poisson compatibili con tali impostazioni.
Nellintrodurre i vari concetti abbiamo anche visto come siano coerenti con alcune interpretazioni
siche: dal concetto di valore medio, autovalore, no al principio dindeterminazione di Heisenberg.
Questultimo caso mette in gran risalto le osservabili Q e P, dalla cui proprietà formale [Q, P] = I
abbiamo dedotto il principio dindeterminazione.
Ma come sono deniti esplicitamente Q e P?
`
E giunto il momento di scendere un po pi` u nel
concreto e di denire compiutamente tali osservabili.
`
E un passaggio fondamentale perche la quan-
tizzazione di Q e P permetterà di denire anche la quantizzazione dellhamiltoniana H (che,
ricordiamo, sicamente rappresenta lenergia).
3.6.1 Quantizzazione di Q
Questa è loperazione pi` u semplice. Dobbiamo denire Q : D(Q) X X. Ricordiamoci anzitutto
che gli elementi di X sono distribuzioni di probabilità (una volta normalizzate) che ci danno in-
formazione sulla localizzazione della particella. In ambito classico la particella è individuata da un
numero q che ne determina la posizione nello spazio. Non è dicile costruire una distribuzione di
probabilità che traduca ciò: lo stato dovrà essere tale che
_
b
a
[(x)[
2
dx =
_
0 se q / [a, b]
1 se q [a, b].
17
Tale stato è rappresentato dalla celebre delta di Dirac q(x), nel senso che (x) = q(x). Ora una
simile funzione, comè noto, non esiste come funzione ordinaria, bens` come funzione generalizzata.
Procediamo formalmente, come se q X. Allora chiaramente
(Qq)(x) =
_
q se x = q
0 se x ,= q
_
= qq(x) = xq(x).
Il primo e lultimo membro delleguaglianza precedente si leggono, estesi ad ogni stato, come
[Q](x) = x(x), x R. (3.6)
Assumiamo quasta come denizione di Q.
`
E da notare che anchè Q X bisogna che
_
R
[Q(x)[
2
dx =
_
R
x
2
[(x)[
2
dx.
Lesistenza di questo integrale in genere non è garantita dal fatto che X comè facile vedere.
Questo signica che Q non sarà denito su tutto X, ma avrà un dominio:
D(Q) :=
_
X :
_
R
x
2
[(x)[
2
dx <
_
.
Questo fatto si porta appresso una complicazione non da poco, cioè che come trasformazione da X
in X, Q non è continuo (esercizio). Non ci occuperemo di questo aspetto se non per commentare in
seguito, dopo lintroduzione anche di P, che lequazione [Q, P] = I già contiene questo spiacevole
imprevisto.
Notiamo, per concludere, che Q è unosservabile reale:
(Q, ) =
_
R
x(x)(x)dx =
_
R
(x)x(x)dx = (, Q).
3.6.2 Quantizzazione di P
Cerchiamo di costruire P in modo tale che valga lidentità fondamentale
QP PQ = ihI.
Avendo già costruito Q ci si può attendere che la precedente sia una sorta di equazione per P.
Vediamo pi` u concretamente lequazione, applicandola allo stato generico :
QP PQ = ih.
Ora Q(x) = x(x). Possiamo riscrivere lidentità precedente come
8
P(x(x)) = x[P](x) ih.
Ora unidentità come quella appena scritta ricorda le proprietà di derivata di un prodotto, dove P
è loperazione di derivazione. In altre parole: poniamo
[P](x) := ih
(x). (3.7)
`
E ora immediato vericare che con questa posizione lidentità fondamentale di commutazione è
soddisfatta.
Abbiamo dedotto una denizione di P di modo tale che lidentità fondamentale fosse soddisfatta.
Tutto ciò potrebbe sembrare un po astratto. Tuttavia P sta al momento della particella come Q
sta alla posizione. In eetti se q(t) è la posizione della particella,
q(t)
è lo stato corrispondente.
8
Ad essere rigorosi andrebbe riscritta come
[P( ()] (x) = x[P](x) ih(x),
ma chiaramente cos` la notazione sarebbe molto pi` u pesante.
18
Supponiamo che t t0. Allora q(t) q(t0) +p(t t0), ove p = q(t0). Pertanto
q(t)

q(t
0
)+p(tt
0
)
.
In altre parole un momento p fa traslare la funzione donda. Sostituendo la con la generica
avremo un usso di stati
M
(x) = (x +)
La generalizzazione della formula q(t) q(0) +tp è data dalla formula di Taylor:
M
(x) (x) +
(x).
Possiamo allora, per analogia con il caso classico, pensare che
(x) sia, a meno di costanti, il

momento generalizzato di . La costante va scelta di modo che la regola di commutazione con Q
valga oppure imponendo che P sia osservabile reale.
Osserviamo, come già per Q, che P non sarà denito su tutto X, ma avrà un dominio
D(P) =
_
X :
,
_
R
[
(x)[
2
dx <
_
.
Tale dominio è pi` u dicile da identicare del dominio di Q. Infatti non è chiaro quali condizioni su
X determinino lesistenza (ed in che senso) di
. Per esempio C
c
è sicuramente in D(P),
ovvero C
c
D(P). Su tale parte del dominio è facile vedere che P è reale: si tratta della formula
dintegrazione per parti. Se infatti , C
c
allora
(P, ) =
_
R
ih
(x)(x)dx
= [ih(x)(x)]
x=+
x=
+ih
_
R
(x)
(x)dx
=
_
R
(x)(ih
(x))dx = (, P).
Chiudiamo questa sezione osservando che il fatto che sia Q che P risultino non continui non è una
sorpresa, ma è profondamente legato alla equazione fondamentale di commutazione e questo è un
fatto puramente algebricotopologico! Infatti:
Teorema 3.12 Se Q, P soddisfano la relazione
QP PQ = ihI,
allora almeno uno dei due deve essere illimitato
(9)
(ovvero discontinuo).
Dim. Osserviamo anzitutto che
Q
n
P = Q
n1
QP = Q
n1
(PQ+ihI) = Q
n1
PQ+ihQ
n1
= Q
n2
(QP)Q+ihQ
n1
= Q
n2
(PQ+ihI)Q+ihQ
n1
= Q
n2
PQ
2
+i2 hQ
n1
.
.
.
= PQ
n
+inhQ
n1
,
cos` che
Q
n
P PQ
n
= inhQ
n1
.
Similmente P
n
Q QP
n
= inhP
n1
. Ora: se Q e P fossero continui (cioè le rispettive norme
operatoriali fossero nite) avremmo che
nh|Q
n1
| = |Q
n
P PQ
n
| |Q
n1
||QP|+|PQ||Q
n1
|, = nh |QP|+|PQ|, n N.
Essendo n arbitrario si ha una contraddizione.
9
Ricordiamo qui che un operatore L : X X si dice limitato se è continuo. In tal caso e solo in questo
è ben denita la norma operatoriale
|L| := sup
jj
X
1
|L|
X
.
Direttamente dalla denizione segue che |L|
X
|L|||
X
per ogni X. Inoltre |LM| |L||M|.
19
3.6.3 Quantizzazione di H
Tutto sommato questa è la parte facile del lavoro. Infatti lidea è sbalorditivamente semplice. Pren-
diamo lhamiltoniana classica del sistema, cioè la funzione H H(q, p) che descriverebbe in contesto
classico la dinamica del sistema secondo le equazioni (2.4). Lidea è di sostituire alle coordinate
generalizzate classiche q e p quelle quantistiche Q e P. Si tratta cioè di vedere come costruire una
funzione di operatori. In alcuni casi questoperazione è semplice. Supponiamo ad esempio che f(q)
sia un polinomio in q,
f(q) = a0 +a1q +a2q
2
+. . . +anq
n
.
`
E facile costruire lespressione f(Q) ponendo
f(Q) = a0I +a1Q+a2Q
2
+. . . +anQ
n
,
dove le potenze sono semplicemente la composizione. In particolare, tenendo conto del fatto che
Q(x) := x(x) avremo che
Q
n
(x) = x
n
(x), = [f(Q)] (x) = a0(x) +a1x(x) +. . . +anx
n
(x) = f(x)(x),
cos` che f(Q) altro non è che loperatore di moltiplicazione per f se f è un polinomio. In generale,
se f è una funzione arbitraria, possiamo assumere che
[f(Q)] (x) := f(x)(x),
cioè che f(Q) sia loperatore di moltiplicazione per f. Lo stesso discorso potrebbe essere formalmente
ripetuto per una funzione di p. Nuovamente: se g(p) = a0 + a1p + a2p
2
+ . . . anp
n
è un polinomio,
allora potremmo porre
g(P) = a0 +a1P +. . . +anP
n
.
Osservato che
[P
n
] (x) = (ih)
n
d
n
dx
n
(x) = (ih)
n
(n)
(x).
In questo caso g(P) diventa unoperatore dierenziale. Se però g non è un polinomio le cose si
complicano notevolmente. Se g(p) = sin p cosa sarebbe sin P? Oppure P
1
3
? Questo è un problema,
cos` come è un problema il fatto che noi dobbiamo quantizzare la funzione H che dipende con-
giuntamente da q e p. Se si pensa al caso di una del tipo H(q, p) = qp ci simbatte nel problema che,
se nei numeri qp = pq tra gli operatori QP ,= PQ! E dunque non è chiaro quale sia (ammesso che ce
ne sia una) la funzione da quantizzare. Fortunatamente, nella meccanica quantistica, tutte queste
sono chiacchiere superabili facilmente perche la dipendenza da q e p è separata e non compaiono
funzioni strane della p. Vedremo, tuttavia, che quando si passerà a quantizzare i campi allora il
problema si porrà in maniera fondamentale.
Prendiamo allora lhamiltoniana dellinizio:
H(q, p) =
1
2m
p
2
+V (q). (3.8)
Ora la sostituzione formale produce:
1(Q, P) 1 =
1
2m
P
2
+V (Q).
Quindi almeno il problema della non commutatività fra Q e P non si pone. Per quanto detto sopra
[P
2
](x) = (ih)
2
(x) = h
2
(x),
mentre
[V (Q)](x) = V (x)(x).
Ciò detto la quantizzazione di H è compiuta:
1 :=
h
2
2m
d
2
dx
2
+V , (3.9)
ovvero, sulla funzione donda
1 =
h
2
2m
(x) +V (x)(x).
Osserviamo che C
c
D(1) e che 1 è simmetrico (quindi è unosservabile reale) su C
c
.
20
3.7 Equazione di Schrodinger
Vogliamo ora determinare le equazioni di evoluzione degli stati e delle osservabili. Avendo introdotto
le parentesi di Poisson [, ] e avendo quantizzato le osservabili fondamentali Q, P, 1 assumeremo
come base di partenza che levoluzione di una generica osservabile sia descritta dallequazione di
Heisenberg:
Assioma 3.13 Levoluzione Ft di unosservabile è governata dallequazione
Ft = [Ft, 1] = [F, 1]t

Nel formalismo classico levoluzione delle osservabili è descritta, equivalentemente, conoscendo il
moto nello spazio delle fasi dalla regola
ft(q, p) = f(Tt(q, p)),
dove |Tt
tR
è il usso ad un parametro di dieomorsmi dello spazio delle fasi, determinato
dalla risoluzione delle equazioni di Hamilton. Qui non disponiamo delle equazioni di Hamilton,
ma potremmo generalizzare la precedente posizione per legare il moto degli stati a quello delle
osservabili. Se infatti lespressione ft(q, p) =valore dellosservabile f al tempo t nello stato (q, p),
potremmo sostituire tale espressione con Ft) =valore medio dellosservabile F al tempo t sullo
stato . Dunque avremmo una nuova equazione
Ft) = F)t
, (3.10)
dove F = F0. Il primo fatto interessante è il seguente:
Proposizione 3.14 (conservazione dellenergia ed unitarietà della dinamica)
1)t
= 1), |t| = ||.
Dim. Infatti:
d
dt
1)t
=
d
dt
1t) =
_
d
dt
1t,
_
= ([1, 1]t, ) = 0.
Per la seconda basta osservare che |t|
2
= Id)t
e ripetere largomento
(10)
.
Si può andare oltre. Scriviamo T(t) := t. Lunitarietà signica che |T(t)| = ||, ovvero
(T(t), T(t)) = (, ), X.
In eetti T(t) non lascia invariate solo le lunghezze in X ma anche gli angoli, nel senso che
Proposizione 3.15
(T(t), T(t)) = (, ), , X.
Dim. Basta ricordare lidentità di polarizzazione
(, ) =
1
4
_
| +|
2
| |
2
+i| +i|
2
i| i|
2
.
Allora
(T(t), T(t)) =
1
4
_
|T(t)( +))|
2
|T(t)( )|
2
+i|T(t)( +i)|
2
i|T(t)( i)|
2
=
1
4
_
| +|
2
| |
2
+i| +i|
2
i| i|
2
= (, ).
10
Pi` u in generale osserviamo che se F è unosservabile tale che [F, 1] = 0, che nella fattispecie signica F
commuta con 1, allora i valori medi di F si conservano; se si osserva che nel caso della meccanica classica
la condizione f, H esprime il fatto che f è un integrale primo per le equazioni di Hamilton, potremmo
intendere la condizione suddetta sulle osservabili come condizione caratteristica degli integrali primi nella
versione quantistica.
21
In modo perfettamente identico introduciamo la forma bilineare a(, ) = (1, ). Questo è una
sorta di prodotto scalare che viene lasciato inalterato dalla dinamica:
Proposizione 3.16
a (T(t), T(t)) = a(, ), , D(1).
Dim. Simile alla precedente.
Reintroducendo lenergia, la proposizione precedente aerma che
(1T(t), T(t)) = (1, ) , , D(1).
In termini geometrici T(t) è una rotazione in X che lascia invariati gli angoli calcolati sia
rispetto allenergia che rispetto al prodotto scalare di X. Verrebbe dunque da pensare T(t) come una
matrice unitaria. Al momento non è però nemmeno evidente che debba essere lineare. Mostriamo
questo fatto.
Proposizione 3.17
T(t) L(X), t R.
Dim. A titolo di esempio mostriamo ladditività. Chiamiamo T := T(t), T
1
= T(t). Dalla
proposizione 3.15 abbiamo che
(T(1 +2), ) =
_
1 +2, T
1
_
=
_
1, T
1
_
+
_
2, T
1
_
= (T1, ) + (T2, )
= (T1 +T2, ) .
Dunque: T(t) è unisometria lineare che deve conservare il prodotto dellenergia. Non è inoltre
dicile osservare che |T(t)
tR
è un gruppo ad un parametro di tali isometrie, nel senso che
T(t +s) = T(t)T(s) e T(0) = I. Invero, osservato che
F)
T(t+s)
= Ft+s) = (Ft)s) = Ft)
T(s)
= F)
T(t)T(s)
,
per ogni osservabile F, è facile vericare che T(t +s) = T(t)T(s). Per vedere questo abbiamo il
Lemma 3.18
F) = F)
, F osservabile, = (mod. e
i
)
Dim. Limplicazione inversa è evidente. Per la diretta, basta considerare come operatore F gli
operatori F := (, ) e F := (, ) (operatori di proiezione sui vettori e rispettivamente).
`
E facile vedere che sono osservabili. Applicando il primo la relazione F) = F)
diventa
||
4
= [(, )[
2
, ||
2
= [(, )[,
mentre applicando il secondo si ottiene ||
2
= [(, )[. Siccome e sono unitari ne segue che
[(, )[ = 1. Ora: scriviamo = (, ) +
, dove
è ortogonale a . Se
,= 0, allora per il
teorema di Pitagora
||
2
= |(, )|
2
+|
|
2
> [(, )[
2
||
2
= ||
4
, = || < 1,
che è impossibile. Dunque
= 0 e quindi = (, ) dove [(, )[ = 1 per cui si può scrivere

= e
i
con R.
22
Dunque T(t + s) = e
i
T(t)T(s) con e
i
unitario. Siccome da un punto di vista sico e
i

accettiamo senzaltro che T(t +s) = T(t)T(s).
A questo punto dovremmo attenderci che esista un operatore / simmetrico (unosservabile) tale
che
T(t) = e
it1
.
Questo, con laggiuntiva e naturale ipotesi che t T(t) C([0, +[; X) è il teorema di Stone,
che qui accettiamo
(11)
. Il punto è: chi è /? Un semplice ragionamento svela il mistero. Osserviamo
anzitutto che, presa unosservabile F,
F)
T(t)
=
_
Fe
it1
, e
it1
_
=
_
e
it1
Fe
it1
,
_
= e
it1
Fe
it1
).
In questo modo
Ft = e
it1
Fe
it1
.
Ma Ft risolve lequazione di Heisenberg

Ft = [Ft, 1], mentre
d
dt
_
e
it1
Fe
it1
_
= iLe
it1
Fe
it1
+ie
it1
Fe
it1
/ = i
_
/e
it1
Fe
it1
e
it1
Fe
it1
/
_
= h
_
/, e
it1
Fe
it1
=
_
e
it1
Fe
it1
, h/
.
Allora deve essere
_
e
it1
Fe
it1
, h/
= [Ft, 1] ,
che per t = 0 si riduce a [F, h/] = [F, 1], per ogni osservabile F, ovvero [F, h/ 1] = 0 F
osservabile.
Lemma 3.19
[F, G] = 0, F osservabile, G = cI.
Dim. Supponiamo che esista una ,= 0 tale che G = c +
, dove
,= 0 è ortogonale a
. Vogliamo costruire unosservabile F tale che [F, G] ,= 0, ovvero FG GF ,= 0. Per fare questo
osserviamo che
(FGGF) = F
_
c +
_
GF = cF +F
GF.
Deniamo in modo lineare F di modo che F = , F
= 2
e F = 0 sul complementare
ortogonale. Allora
(FGGF) = c + 2
G = c + 2
,= 0.
Dunque G = c per ogni X. Ora supponiamo che G1 = c11, G2 = c22, con 1 e 2
perpendicolari ed unitari. Mostriamo che c1 = c2. Invero consideriamo 1 +2. Deve esistere c tale
che G(1 +2) = c(1 +2). Ma G(1 +2) = c11 +c22, da cui
c1 +c2 = c11 +c22.
Ma questo è evidentemente possibile se e solo se c1 = c = c2.
Allora / =
1
h
1+cI dove c è reale (perche sia un osservabile), e quindi
T(t) = e
i
h
t(;+cI)
.
Questo signica che
T(t) =
i
h
(1+cI) T(t) =
i
h
1T(t)
ic
h
T(t),
d
dt
_
e
ic
h
t
T(t)
_
=
i
h
e
ic
h
t
1T(t),
11
Cosa esattamente signichi e
it1
non lo specichiamo qui; in generale L non è un operatore continuo per
cui lesponenziale non viene denito attraverso la serie esponenziale. Quello che ci interessa è che abbia le
stesse propriet` a formali dellesponenziale come se / fosse unoperatore lineare continuo.
23
ovvero che (t) = e
ic
h
t
T(t) risolve
(t) =
i
h
1(t), (t) = e
i
h
t;
(0), T(t) = e
i
c
h
t
e
i
h
t;
.
Nuovamente, siccome il fattore e
i
c
h
t
è immaginario puro e e
i
c
h
t
e
i
h
t;
e e
i
h
t;
rappresentano
lo stesso stato, poniamo c = 0 ed abbiamo
T(t) = e
i
h
t;
.
Abbiamo cioè il
Teorema 3.20 La (3.10) è valida se e solo se t è soluzione dellequazione di Schrodinger
t =
i
h
1t. (3.11)
Osservazione 3.21 Sosituendo lespressione (3.9) nella (3.11) si trova:
iht(t, x) =
h
2
2m
xx(t, x) +V (x)(t, x).
La soluzione dellequazione di Schrodinger viene indicata con la scrittura
t = e
i
h
t;
.
Vale la pena di osservare che loperatore di Schrodinger
i
h
1 è antisimmetrico essendo
_
i
h
1,
_
=
i
h
(1, ) =
i
h
(, 1) =
_
,
i
h
1
_
,
per cui loperatore e
i
h
t;
è unitario, per quanto visto già nel Corollario 2.7. Inoltre, di speciale
importanza sono gli stati nei quali lenergia 1 assume un valore certo , vale a dire gli autostati
tali che 1 = . Infatti, per tali stati levoluzione è molto semplice: procedendo formalmente
avremmo
e
i
h
t;
=
n
_
i
h
t
_
n
n!
1
n
=
n
_
i
h
t
_
n
n!

n
= e
i
h
t
.
Sebbene apparentemente tale identità poggi sul nulla, la risposta nale è corretta perche se u(t, x) =
e
i
h
t
(x) allora
tu(t, x) =
i
h
e
i
h
t
(x) =
i
h
e
i
h
t
(1)(x) =
i
h
_
1e
i
h
t
_
(x) =
i
h
1u(t, )(x)
=
i
h
_
h
2
2m
xxu(t, x) +V (x)u(t, x)
_
,
ovvero u risolve lequazione di Schrodinger. Il fatto interessante è che la formula u(t, x) = e
i
h
t
(x)
illustra molto bene lunitarietà ed il fatto che lo stato iniziale non viene modicato in ampiezza
quanto in fase (spiegando a posteriori i fenomeni di interferenza citati allinizio). Per fare un
ulteriore passo osserviamo che se poi abbiamo un sistema |n
nN
di autostati per 1 relativi ad
autovalori |n
nN
, sistema che sia una base ortonormale per X
(12)
, allora possiamo ricostruire
integralmente la soluzione dellequazione di Schrodinger attraverso uno sviluppo in serie. Infatti
basterà osservare che
e
i
h
t;
=
n
cne
i
h
t;
n =
n
cne
i
h
tn
n.
Dunque costruire una base ortonormale di autofunzioni per lhamiltoniana quantistica permette di
risolvere numerosi altri problemi, ivi compresa levoluzione degli stati (che è ovviamente il problema
fondamentale). Diventa pertanto un problema matematico che è interessante arontare.
12
Cioè tale le n siano unitarie, perpendicolari (nel senso che (n, m) = 0 se n ,= m) e che ogni altra
X si scriva =
nN
cnn. In tal caso cn = (, n).
24
3.8 LOscillatore Armonico
Con oscillatore armonico chiameremo il caso di un sistema quantistico la cui hamiltoniana classica
corrisponda a quella appunto di un oscillatore armonico, cioè
H(q, p) =
1
2m
p
2
+

2
q
2
.
Lanalisi di questo caso è fondamentale per diversi motivi. Anzitutto costituisce un esempio non
banale completamente calcolabile
(13)
che permette di vedere in maniera limpida come la teoria
permetta di spiegare la stabilità della struttura della materia. In secondo luogo costituisce il punto
di partenza per la costruzione del cosidetto campo libero, che può essere immaginato come una
sovrapposizione di inniti oscillatori armonici. Inne è anche il punto di partenza per le cosidette
perturbazioni, vale a dire dei casi con esergia potenziale V somma di quella di oscillatore armonico
1
2
q
2
con unenergia potenziale V1(q).
Normalizzando opportunamente le costanti (prenderemo m = = 1) consideriamo lhamiltoniana
classica
Hosc(q, p) =
1
2
(q
2
+p
2
),
corrispondente a quella quantistica
1osc :=
h
2
2
d
2
dx
+
1
2
x
2
.
Due sono le questioni che aronteremo: i possibili valori dellenergia e la soluzione dellequazione di
Schrodinger (3.11).
3.8.1 Analisi spettrale
I valori dellenergia sono gli autovalori dellhamiltoniana, come abbiamo detto nella sezione 3.5.
Chiameremo spettro puntuale di 1osc linsieme
p(1osc) := | R : è autovalore per 1osc .
In questa sezione dimostreremo il seguente
Teorema 3.22
p(1osc) =
_
h
_
1
2
+n
_
: n N |0
_
.
Inoltre: per ogni p(1osc) lautospazio relativo allautovalore ha dimensione 1.
Osservazione 3.23 (Interpretazione) Il teorema 3.22 dice che lenergia assume solo un innità
discreta di valori, in forte contrasto con le proprietà classiche dellenergia. Tuttavia questo non è
aatto in contrasto con gli esperimenti di sica atomica ed anzi spiega quel fenomeno assurdo
della quantizzazione dellenergia. Ciascuno degli autostati corrisponderà ad un dierente livello di
energia; verrà mostrato come sarà possibile operare su uno stato per farlo passare da un livello ad
un altro di energia, a scatti, conformemente con lesperienza che mostra lesistenza di precise soglie
di energia oltre le quali è possibile far scattare le particelle da un livello ad unaltro.
La dimostrazione del teorema (3.22) è piuttosto lunga anche se elementare: avremo modo di ap-
prezzare il formalismo introdotto. Cominciamo dallhamiltoniana quantistica
(14)
nella forma
1osc =
1
2
(P
2
+Q
2
).
Osserviamo che se P e Q fossero numeri si avrebbe
P
2
+Q
2
= (QiP)(Q+iP).
13
Vedremo poi cosa sintende con la locuzione completamente calcolabile.
14
Dora innanzi semplicemente lhamiltoniana
25
Tuttavia Q e P sappiamo non commutano, per cui lordine in un prodotto è importante. Osserviamo
allora che
(QiP)(Q+iP) = Q
2
+i(QP PQ) +P
2
= Q
2
+P
2
hI = 21osc hI
ovvero
1osc =
1
2
(QiP)
1
2
(Q +iP) +
h
2
I = A
+
h
2
I, (3.12)
ove gli operatori A
e A
sono deniti dalla fattorizzazione del secondo membro della (3.12). Tali
operatori vengono detti (per una ragione che sarà chiara fra poco) rispettivamente di creazione ed
distruzione. Non sono osservabili reali, ma sono legati fra loro dalla relazione
Lemma 3.24
(A
, ) = (, A
), , X,
ovvero A
=
_
A
.
Dim. Ricordato che Q e P sono osservabili e che il prodotto su X è hermitiano abbiamo:
((QiP), ) = (Q, ) i(P, )
= (, Q) i(, P)
= (, (Q +iP)).
La fattorizzazione (3.12) si rivelerà importantissima. Tanto per cominciare da qui in poi indicheremo
semplicemente con A loperatore di creazione ed, in virt` u del lemma precedente, A
loperatore di
distruzione.
Proposizione 3.25 Se 0 X è tale che
A
0 = 0,
allora
1osc0 =
h
2
0.
Lo stato 0 si dice stato fondamentale.
Dunque è utile risolvere A
0 = 0
(15)
. Scriviamo questa equazione
A
0 = 0 (Q +iP)0 = 0 x0(x) + h
(x) = 0.
Si tratta di una semplice equazione dierenziale la cui soluzione generale è
0(x) = Ke
1
2 h
x
2
.
`
E evidente che 0 X. Scegliamo K di modo tale che |0| = 1. Otteniamo:
0(x) = (h)
1/4
e
1
2 h
x
2
.
Facciamo qualche considerazione sul signicato di 0. Tornando allinterpretazione originaria,
rispetto allo stato 0 abbiamo che
_
b
a
[0(x)[
2
dx =
1
h
_
b
a
e
x
2
h
dx = A
_
0,
h
2
_
([a, b]),
15
Con linterpretazione di A
come operatore di distruzione,

0
è lo stato di energia minima, caratterizzato
dal fatto che, levandogli ununit` a (quanto) di energia, cessa di esistere. Una volta trovato
0
costruiremo
tutti gli altri autostati successivamente aggiungendo energia, attraverso A.
26
2
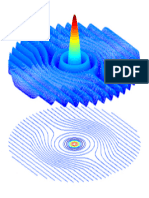
Figure 1: La distribuzione di probabilità associata a 0.
cioè in termini della distribuzione di probabilità [0[
2
essa è una gaussiana di media 0 e varianza
h
2
. Lo stato 0 corrisponde allo stato di quiete, se osserviamo che
Q)
0
= (Q0, 0) =
_
R
(Q0)(x)0(x) dx =
_
R
x0(x)
2
dx = 0,
e
P)
0
=
_
R
ih
0
(x)0(x) dx = ih
_
R
2
h
x0(x)
2
dx = 0.
Inoltre è lo stato di energia minima. Infatti se è un autostato unitario per 1, 1 = , allora
= 1) = AA
+
h
2
I) = AA
) +
h
2
||
2
= |A
|
2
+
h
2
>
h
2
,
a meno che A
= 0, che vuol dire = 0.

Procediamo ora nella determinazione degli altri autovalori dellenergia. Prima di immergerci nei
calcoli vediamo qualche utile identità:
Lemma 3.26
[A, A
] = iI, [1osc, A] = iA.

Dim. Si tratta di semplici veriche. Abbiamo
ih[A, A
] = (AA
A) =
1
2
[(QiP)(Q+iP) (Q +iP)(QiP)]
=
1
2
_
Q
2
+iQP iPQ+P
2
_
Q
2
+P
2
+iPQiQP
_
= i (QP PQ)
= i ih[Q, P]
= hI,
da cui segue la prima. Per la seconda abbiamo
ih[1osc, A] =
_
AA
+
h
2
I
_
A A
_
AA
+
h
2
I
_
= A(A
AAA
)
= A ih[A
, A]
= hA.
27
Proposizione 3.27
1oscA0 = h
_
1 +
1
2
_
A0.
Dim. Basta applicare il lemma 3.26:
1oscA0 = (1oscAA1osc +A1osc) 0 = ih[1osc, A]0 +
h
2
A0 = h
_
1 +
1
2
_
A0.
Poniamo:
1 :=
A0
|A0|
.
Morale: 1 X, |1| = 1 e 1osc1 = h
_
1 +
1
2
_
1. Ora iteriamo il procedimento. Abbiamo prima
però bisogno di estendere il lemma 3.26:
Lemma 3.28
[1osc, A
n
] = inA
n
.
Dim. Per induzione. Sia vera per n 1:
1oscA
n
= 1oscA
n1
A
=
_
A
n1
1osc +ih[1osc, A
n1
]
_
A
=
_
A
n1
1osc + h(n 1)A
n1
_
A (hp dinduzione)
= A
n1
(A1osc +ih[1osc, A]) + h(n 1)A
n1
A
= A
n
1osc + hA
n1
A+ h(n 1)A
n
= A
n
1osc + hnA
n
.
Dunque
1oscA
n
0 = A
n
1osc0 +ih[1osc, A
n
]0 =
h
2
A
n
0 + hnA
n
0 = h
_
1
2
+n
_
A
n
0,
per cui, posto
n :=
A
n
0
|A
n
0|
, (3.13)
risulta che n è autostato relativo allautovalore n := h
_
1
2
+n
_
. Per il momento sembra tutto
piuttosto astratto. Vediamo quindi le proprietà del sistema |n e cerchiamo di comprendere come
sono fatte le n.
Proposizione 3.29
n m, n ,= m
Dim. n m signica (n, m) = 0. Formiamo dunque il prodotto scalare:
n(n, m) = (1oscn, m) = (n, 1oscm) = (n, m)m,
da cui
(n m)(n, m) = 0.
Ma siccome n ,= m se n ,= m questo è possibile se e solo se n m.
28
Proposizione 3.30
|A
n
0| =
h
n
n!. (3.14)
Dim. Dal lemma 3.24 segue che
|A
n
0|
2
= (A
n
0, A
n
0) = ((A
)
n
A
n
0, 0).
Applicando ripetutamente la prima delle identità del lemma 3.26 si trova che
(A
)
n
A
n
= (A
)
n1
A
AA
n1
= (A
)
n1
(AA
+ih[A
, A]) A
n1
= (A
)
n1
(AA
+ hI) A
n1
= h(A
)
n1
A
n1
+ (A
)
n1
AA
A
n1
= h(A
)
n1
A
n1
+ (A
)
n1
A(A
A)A
n2
= h(A
)
n1
A
n1
+ (A
)
n1
A(AA
+ih[A
, A]) A
n2
= h(A
)
n1
A
n1
+ (A
)
n1
A(AA
+ hI) A
n2
= 2h(A
)
n1
A
n1
+ (A
)
n1
A
2
A
A
n2
.
.
.
= nh(A
)
n1
A
n1
+ (A
)
n1
A
n
A
.
Applicando tutto a 0 e tenendo conto che A
0 = 0,
(A
)
n
A
n
0 = nh(A
)
n1
A
n1
0 = n(n 1) h
2
(A
)
n2
A
n2
0 = . . . = n!h
n
0.
da cui la conclusione.
Proposizione 3.31
An =
_
h(n + 1)n+1, A
n =
hnn1.
Dim. Proviamo solo una delle identità (la dimostrazione dellaltra è identica).
An = A
_
1
h
n
n!
A
n
0
_
=
1
h
n
n!
A
n+1
0
=
_
h
n+1
(n + 1)!
h
n
n!
n+1 =
_
h(n + 1)n+1.
`
E proprio questa proposizione che fornisce linterpretazione degli operatori di creazione ed dis-
truzione, come abbiamo detto in precedenza. Passiamo ora in concreto a descrivere le funzioni n.
Già conosciamo 0, denita dalla formula
0(x) = ( h)
1/4
e
x
2
2 h
. (3.15)
Calcoliamo n. Dalla (3.13) e dalla proposizione 3.30 abbiamo
n =
1
2
n
h
n
n!
(QiP)
n
0,
29
bella formula ma abbastanza criptica! Cerchiamo di intuire la forma di (Q iP)
n
0. Osserviamo
che
(QiP)0(x) = x0(x) i(ih
0
(x)) = x0(x) h
0
(x)
= x0(x) h
_
x
h
_
0(x)
= 2x0(x)
=: p1(x)0(x),
dove p1(x) = 2x. Proviamo ancora:
(QiP)
2
0(x) = (QiP)[2x0(x)] = 2x
2
0(x) h(2x0(x))
= 2x
2
0(x) h
_
20(x) + 2x
_
x
h
_
0(x)
_
= (4x
2
2 h)0(x)
=: p2(x)0(x),
dove p2(x) = 4x
2
2 h.
2
Figure 2: Le distribuzioni di probabilità associate a 0, 1, 2.
Possiamo pertanto congetturare che n(x) =
1
2
n
h
n
n!
pn(x)0(x), dove pn è un opportuno poli-
nomio di grado n. Infatti
n+1(x) =
1
h(n+1)
1
2
(QiP)n =
1
2
n+1
h
n+1
(n+1)!
_
xpn(x)0(x) h(pn(x)0(x))
_
=
1
2
n+1
h
n+1
(n+1)!
_
xpn(x) h
_
p
n
(x)
x
h
pn(x)
__
0(x)
=
1
2
n+1
h
n+1
(n+1)!
(2xpn(x) hp
n
(x)) 0(x).
Questa formula, oltre che confermare quanto supposto sopra, dice anche che
pn+1(x) =
_
2xpn(x) hp
n
(x)
_
.
I polinomi pn vengono chiamati polinomi di Hermite e possono essere ricavati iterando pi` u volte
la formula precedente. Osserviamo anche che
A
n =
hnn1 =
hn
1
_
2
n1
h
n1
(n 1)!
pn1(x)0(x).
Daltra parte
A
n =
1
2
(Q +iP)n =
1
2
(xn + h
n
)
=
1
2
1
2
n
h
n
n!
_
xpn + h
_
p
x
h
pn
__
0
=
h
2
n+1
h
n
n!
p
n
0.
30
Mettendo assieme le due relazioni precedenti otteniamo
h
2
n+1
h
n
n!
p
n
(x) =
hn
1
_
2
n1
h
n1
(n 1)!
pn1(x), p
n
(x) = 2npn1(x).
3.8.2 La formula di Mehler
Vogliamo ora andare a studiare la soluzione dellequazione di Schrodinger. Abbiamo visto quanta
importanza abbia la conoscenza di una base ortonormale per X di autovettori di 1osc. Si può
dimostrare che le autofunzioni |n
nN
trovate nella sezione precedente hanno questa proprietà
che qui, senzaltro aggiungere, daremo per buona.
Consideriamo dunque la soluzione u(t) := e
i
h
t;osc
dellequazione di Schrodinger con dato
iniziale . Abbiamo precedentemente visto che, almeno formalmente, si ha
u(t, x) =
n
(, n)e
i(
1
2
+n)t
n(x) =
n
_
R
(y)n(y) dy e
i(
1
2
+n)t
n(x)
=
_
R
(y)
_
n
e
i(
1
2
+n)t
n(y)n(x)
_
dy
=
_
R
(y)kt(x, y) dy.
La funzione kt viene detta propagatore. La rappresentazione integrale è molto pi` u comoda di
quella di una serie, poiche le tecniche di calcolo per gli integrali sono molto pi` u semplici e ranate
di quelle per le serie, cos` che appunto una rappresentazione integrale della soluzione è quanto di
meglio ci si possa attendere. Fisicamente il propagatore ha un signicato ben preciso. Se è la
funzione donda al tempo t = 0, il propagatore è un sistema di pesi che deforma la funzione donda
secondo la sica del sistema. Ragionando rozzamente (ma ecacemente) ed immaginando come
una distribuzione di probabilità e u(t, ) la sua corrispondente nel futuro (se per esempio t > 0)
allora kt è la ricetta attraverso cui dobbiamo modicare per ottenere u(t, ). Immaginiamo per
esempio che sia molto concentrata intorno ad un certo x0. Per eccesso, = x
0
. Allora
u(t, x) =
_
R
x
0
(y)kt(x, y) dy = kt(x, x0),
cioè kt(x, x0) viene ad assumere il signicato di probabilità di trovare al tempo t nel punto x una
particella partita al tempo 0 dal punto x0. Naturalmente sappiamo che questa interpretazione non è
corretta: ne ne kt sono distribuzioni di probabilità; sono addirittura funzioni a valori complessi.
Ma il senso, pi` u o meno, è questo.
Per loscillatore armonico è possibile determinare esattamente la forma esplicita del propagatore,
ed è quello che ora faremo. Osserviamo preliminarmente che
n
e
i(
1
2
+n)t
n(y)n(x) = e
i
t
2
_
n
e
int
2
n
h
n
n!
pn(x)pn(y)
_
0(x)0(y)
= e
i
t
2
_
n
_
e
it
2 h
_
n
n!
pn(x)pn(y)
_
0(x)0(y),
cos` che è conveniente introdurre la funzione
(, x, y) :=
n
n!
pn(x)pn(y).
Supponiamo ora di poter fare tutti i conti del caso (cosa che può essere vericata con un minimo
31
di pazienza) e cerchiamo unequazione dierenziale per . A tal proposito osserviamo che
x =
n
n!
p
n
(x)pn(y) =
n
n!
2npn1(x)pn(y)
= 2
n1
(n 1)!
pn1(x)
_
2ypn1(y) hp
n1
(y)
_
= 4y
n1
(n 1)!
pn1(x)pn1(y) 2 h
n1
(n 1)!
pn1(x)p
n1
(y)
= 4y2hy,
ovvero x+2hy = 4y. Anche se non si tratta di unequazione ordinaria possiamo ricondurla
facilmente ad una di quel tipo se osserviamo che a sinistra cè la derivata direzionale lungo il vettore
(1, 2 h). Poniamo allora
(x) := (, x, 2 hx +), R.
Risulta subito che
(x) = 4(2 hx +)(x), da cui

(x) = (0)e
4( hx
2
+x)
, = (, x, y) = (, 0, y 2 hx)e
4 h
2
x
2
+4xy
.
Calcoliamo ora (, 0, y) =
n
n!
pn(0)pn(y). Osserviamo che pn(0) è il termine noto del polinomio
pn e che p0(0) = 1 e p1(0) = 0. In generale,
pn(y) = 2ypn1(y) hp
n1
(y) = 2ypn1(y) 2 h(n 1)pn2(y),
da cui
pn(0) = 2 h(n 1)pn2(0) = (1)
2
h
2
(n 1)(n 3)pn4(0) = . . .
`
E pertanto immediato concludere che pn(0) = 0 se n è dispari, mentre per n = 2 abbiamo
p
2
(0) = 2 h(2 1)p
2(1)+1
(0) = (1)
2
2
2
h
2
(2 1)(2 3)p
2(2)+1
(0)
.
.
.
= (1)
(2 1)(2 3) 3 1 = (1)
h
2(21)(22)321
(1)21
= (1)
h
(2)!
!
,
per cui
(, 0, y) =
2
(2)!
p
2
(0)p
2
(y) =
(h
2
)
!
p
2
(y) =: (h
2
, y).
Ripetiamo il tipo di calcolo fatto sopra con . Abbiamo che
y(, y) =
!
p
2
(y) =
!
2(2)p
21
(y) =
!
4
_
2yp
2(1)
hp
2(1)
(y)
_
= 8y
1
(1)!
p
2(1)
(y) 4 hy
1
(1)!
p
2(1)
(y)
= 8y(, y) 4 hy(, y),
da cui
y(, y) =
8
1 + 4h
y(, y), = (, y) = (, 0)e
4
1+4 h
y
2
.
Ora,
(, 0) =
!
p
2
(0) =
!
(1)
h
(2)!
!
=
( h)
!
(2)!
!
=
(2 h)
(21)(23)31
!
=
(4 h)
(21)(23)31
2(22)42
=
(4 h)
(21)!!
(2)!!
,
32
dove si è posto (2 1)!! := (2 1)(2 3) 3 1 e (2)!! := 2(2 2) 4 2. Lo sviluppo
precedente ricorda uno sviluppo notevole. Precisamente
arcsin =
(2 1)!!
(2)!!
2+1
2 + 1
.
Pertanto
(4 h)
(21)!!
(2)!!
=
(21)!!
(2)!!
(
4 h)
2
2+1
(2 + 1)
:=
4 h
=
(21)!!
(2)!!
2
2+1
(2 + 1)
=
(21)!!
(2)!!
d
d
2+1
2+1
=
d
d
arcsin =
1
1
2
=
1
1+4 h
.
Possiamo nalmente tirare le somme di tutti questi calcoli. Abbiamo nalmente che
(, x, y) = (, 0, y 2 hx)e
4 h
2
x
2
+4xy
= (h
2
, y 2 hx)e
4 h
2
x
2
+4xy
= (h
2
, 0)e
4 h
2
14 h
2
2
(y2 hx)
2
e
4 h
2
x
2
+4xy
=
1
_
1 4 h
2
2
e
4 h
2
14 h
2
2
(y2 hx)
2
e
4 h
2
x
2
+4xy
.
Abbiamo nalmente la possibilità di dedurre la formula esplicita per il propagatore, ricordato che
=
e
it
2 h
. Per tale valore di ,
_
e
it
2 h
, x, y
_
=
1
1 e
i2t
e
e
i2t
h(1e
i2t
)
(ye
it
x)
2
e
i2t
h
x
2
+
2e
it
h
xy
,
da cui, pertanto
kt(x, y) = e
i
t
2
1
1 e
i2t
e
e
i2t
h(1e
i2t
)
(ye
it
x)
2
e
i2t
h
x
2
+
2e
it
h
xy
=
1
i2hsin t
e
1
h
e
i2t
(ye
it
x)
2
e
i2t
(1e
i2t
)x
2
+2e
it
(1e
i2t
)xy
1e
i2t
=
1
i2hsin t
e
1
h
e
i2t
(y
2
2e
it
xy+e
i2t
x
2
)e
i2t
(1e
i2t
)x
2
+2e
it
(1e
i2t
)xy
1e
i2t
=
1
i2hsin t
e
1
h
e
i2t
(x
2
+y
2
)+2e
it
xy
1e
i2t
.
Anche se non sia evidente, largomento dellesponenziale è un immaginario puro
e
i2t
(x
2
+y
2
) + 2e
it
xy
1 e
i2t
Teorema 3.32 (formula di Mehler)
kt(x, y) =
1
i2 h sin t
e
1
h
_
y
2
x
2
2

(ye
it
x)
2
1e
i2t
_
. (3.16)
Al di là del fatto emozionale di essere riusciti a calcolare esattamente il propagatore, si pone
subito una domanda: in che modo il propagatore dipende dalla sica del sistema (in particolare dal
potenziale V )? Abbiamo detto, allinizio di questa sezione, che sicamente il propagatore si associa
33
a probabilità di transizione. Il quesito è quindi: come queste probabilità dipendono da V ? A questo
problema risponderà in generale la formula di Feynman, che sarà oggetto della prossima sezione.
Qui ci limitiamo ad un ragionamento poco rigoroso ma ecace.
La prima cosa che si osserva nella (3.16) è che la stessa presenta dei problemi di denizione
in t. Scartando per un momento t = 0, la formula funziona no a che t ]0, [, dopodiche salta
nuovamente. Osserviamo anzitutto che
y
2
x
2
2

(y e
it
x)
2
1 e
i2t
=
(y
2
x
2
)(1 e
i2t
) 2(y
2
+e
i2t
x
2
2e
it
xy)
2(1 e
i2t
)
=
(x
2
+y
2
)(1 +e
i2t
) 4e
it
xy
2(1 e
i2t
)
=
(x y)
2
(1 +e
i2t
) + 2xy
_
1 +e
i2t
2e
it
_
2(1 e
i2t
)
= i
_
(x y)
2
2
cot t xy tan
t
2
_
.
Finora abbiamo fatto manipolazioni puramente formali. Supponiamo adesso che t 0 e sostituiamo
alle espressioni dipendenti da t il loro comportamento asintotico: cot t 0
1
t
, tan
t
2
0
t
2
. Otteniamo
y
2
x
2
2

(y e
it
x)
2
1 e
i2t
i
_
(x y)
2
2t
t
xy
2
_
.
Si potrebbe obiettare che il secondo termine è trascurabile rispetto al primo per t 0. Daltra
parte adesso vediamo che in realtà cos` non è, sicamente parlando. . . Ricordiamo il signicato di
kt(x, y): è la probabilità (pi` u o meno) che una particella che parte al tempo 0 nel punto y al tempo
t si trovi nel punto x. Allora la quantità
xy
t
può essere interpretata come una velocità ed allora
1
2
_
xy
t
_
2
=
(xy)
2
2t
2
è unenergia cinetica. Daltra parte
xy
2

x
2
2
= V (x), cos` che
y
2
x
2
2

(y e
it
x)
2
1 e
i2t
i
_
1
2
_
x y
t
_
2
V (x)
_
t i/(q),
dove ritroviamo una vecchia conoscenza, lazione /! Morale: per t 0
kt(x, y)
1
i2 ht
e
i
h
,(q)
, (3.17)
dove q è una curva di moto tale che q(0) = y e q(t) = x.
Naturalmente questa deduzione è tuttaltro che rigorosa.
`
E interessante perche è un caso partico-
lare della formula di Feynman (che ha pari grado di rigore rispetto a questa). I suoi limiti di validità
sembrano legati a tempi piccoli, che però potrebbero essere aggirati replicando la formula su piccoli
intervalli. Vedremo questa operazione pi` u in generale ed elegantemente nella prossima sezione.
Accenniamo inne ad un ulteriore importantissimo problema. Abbiamo visto col principio din-
determinazione di Heisenberg che la costante h si lega profondamente alla natura quantistica, nel
senso che rappresenta una limitazione dal basso al prodotto degli errori commessi nel misurare Q
e P contemporaneamente. Tali misurazioni sono possibili senza apprezzabili errori (cioè h = 0)
nel caso della meccanica classica. Sorge allora naturale il quesito: cosa succede se h 0? Cioè: è
possibile in qualche senso opportuno, eliminando lostacolo di fondo alla misurazione contemporanea
di posizioni e momenti, ritrovare le traiettorie della meccanica classica? Questo problema va sotto il
nome di limite classico. Per dare unidea della questione riprendiamo il propagatore delloscillatore
armonico.
Ancora una volta partiamo dal signicato morale di kt(x, y):
3.9 Latomo di idrogeno
I calcoli esatti come nel paragrafo precedente si possono fare in un limitatissimo numero di casi,
poiche nei modelli interessanti interviene una complessità notevole. Il caso dellatomo di idrogeno è
34
uno di questi pochi casi che qui ci limiteremo a raccontare (i conti sono tecnicamente elementari come
quelli del caso delloscillatore armonico, anche se un po pi` u complessi). In particolare riporteremo
i risultati teorici e li compararemo con i dati sperimentali. Questo è un punto molto importante,
perche latomo di idrogeno dimostra la correttezza della meccanica quantistica, nel senso che il grado
di concordanza tra dati sperimentali e valori predetti dal modello supera la precisione esistente in
ogni altro ambito della Fisica!
Latomo di idrogeno è composto da un protone di massa mp e carica e (che costituisce il nucleo)
ed un elettrone di massa me e carica e. Trascurando la forza gravitazionale rispetto a quella di
Coulomb, lhamiltoniana classica è data da
H(qp, qe, pp, pe) =
1
2mp
[pp[
2
+
1
2me
[pe[
2
V (qp, qe), V (qp, qe) =
e
2
[qe qp[
.
Qui qp, qe R
3
rappresentano rispettivamente le posizioni del protone e dellelettrone, pp, pe R
3
le rispettive velocità (per cui [pp[
2
= (pp)
2
1
+ (pp)
2
2
+ (pp)
2
3
). Nella sica del sistema è noto anche
che il nucleo è molto pesante rispetto allelettrone, nel senso che mp 2000me, per cui si può
immaginare che di fatto sia lelettrone a muoversi attorno al protone. Secondo le equazioni di
hamilton della Fisica classica lelettrone si muoverebbe pi` u o meno come la Terra attorno al Sole
su orbite circolari/ellittiche. Il problema è che il moto risulterebbe accelerato e, secondo le leggi
dellelettrodinamica classica, si avrebbe una emissione di energia che dovrebbe portare lelettrone
a collassare sul nucleo. Tuttavia questo fenomeno non si osserva nella realtà. Anzi, le osservazioni
sperimentali lasciano intendere che non ci sia una variazione continua dellenergia e che quindi
lelettrone non possa che trovarsi a determinati livelli discreti di energia. Un avvicinamento od
allontanamento dal nucleo sarebbe possibile solo togliendo o fornendo un certo quantitativo di
energia i cui valori sono stati misurati sperimentalmente. Spiegare questo meccanismo e prevedere
i valori possibili dellenergia è stato uno dei motivi per cui è nata la meccanica quantistica.
Seguendo limpostazione data in questa sezione i possibili valori dellenergia sono gli autovalori
dellhamiltoniana quantistica
1 =
1
2mp
P
2
p
+
1
2me
P
2
e

e
2
[qp qe[
dove P
2
p
= (Pp)
2
1
+ (Pp)
2
2
+ (Pp)
2
3
. Per analogia col caso unidimensionale (Pp)
2
i
= ih
(qp)
i
cos` che
1 =
h
2
2mp
qp

h
2
2me
qe

e
2
[qp qe[
,
dove qp
=
3
i=1

(qp)
i
(qp)
i
è il cosiddetto laplaciano. Come si intuisce, risolvere 1 = non
appare un problema semplice
(16)
. Una prima riduzione di complessità del problema può essere fatta
considerando il moto relativo dellelettrone rispetto al protone (vista la dierenza tra le masse), cos`
che il problema è ridotto a trovare gli autovalori dellhamiltoniana
1 =
h
2
2mr
q
e
2
[q[
,
dove mr =
memp
me+mp
, e q = qe qp. Si tratta in ogni caso di un problema complesso perche lequazione
di Schrodinger stazionaria risultante è comunque unequazione a derivate parziali:
h
2
2mr
q(q)
e
2
[q[
(q) = (q).
Ad ogni modo, essendoci una dipendenza da q nel potenziale dalla sola distanza di q dallorigine, si
può pensare di impostare il problema in coordinate sferiche cercando = (r, , ). Ciò porta ad
una riduzione del problema che qui non presentiamo. Il risultato nale è il calcolo degli autovalori
che risultano essere
n =
mre
4
2 h
2
n
2
, n N.
Per n = 1 si ottiene E1 =
mre
4
2 h
il valore dellenergia dello stato fondamentale, valore che coincide
con quello misurato sperimentalmente a meno di un errore di 10
8
!
16
A tal proposito osserviamo che = (qp, qe) è una funzione di 6 variabili reali. . .
35
4 La Formula di Feynman
Abbiamo visto con loscillatore armonico una descrizione completa della meccanica quantistica di
un sistema ad un grado di libertà sottoposto ad un campo di forze elastiche. In generale, sostituendo
allenergia potenziale V (q) =
1
2
q
2
delloscillatore armonico, una qualsiasi energia V non si riuscirà
a descrivere esattamente lo spettro dellhamiltoniana (cioè i valori dellenergia e gli autostati) e
levoluzione dello stato. Ancor pi` u problemi poi si avranno quando si passa da 1 a N gradi di
libertà.
In questa sezione partiremo in generale dal problema di costruire il propagatore per lequazione
di Schrodinger
_
_
_
ihtu(t, x) =
h
2
2m
xxu(t, x) +V (x)u(t, x),
u(0, x) = (x),
cioè la funzione kt(x, y) tale che
u(t, x) =
_
R
(y)kt(x, y) dy.
Già agli albori della teoria della Meccanica Quantistica, Dirac aveva espresso lidea che in generale
il propagatore dovesse dipendere dallazione classica e fosse, in qualche misura, responsabile della
natura ondulatoria del comportamento degli stati. Pi` u precisamente questa idea veniva espressa da
Dirac nella formula kt(x, y) e
i
h
,(q)
dove q è una traiettoria che congiunge y ad x. Eettivamente
abbiamo visto che, nel caso delloscillatore armonico e per tempi piccoli, in via embrionale è
eettivamente cos`.
Leroe della storia divenne a questo punto Feynman, che sviluppò a fondo questa idea in generale
pervenendo alla bellissima formula che porta il suo nome e che in questa sezione illustreremo.
Feynman ha mostrato che addirittura si può basare su questa formula il fondamento di tutta la
Meccanica Quantistica e questi risultati gli sono valsi il Premio Nobel. Sfortunatamente, da un
punto di vista puramente matematico, la formula di Feynman è priva di fondamento, e nel corso di
diverso tempo i tentativi di darle un senso sono risultati insoddisfacenti. Si deve a Kac losservazione
che la formula di Feynman può essere resa rigorosa non appena si trasforma, con un cambiamento
di coordinate, il tempo t reale ad immaginario, convertendo il propagatore k in quello relativo
allequazione del calore, che va a sostituire quella di Schrodinger. Questa operazione getta un ponte
importante con la teoria dei processi stocastici ed, in particolare, coi processi di diusione, le cui
tecniche sono state sviluppate a partire dagli anni trenta del 900 da Kolmogorov, Ghihman e Ito e
che si basa oggi su unampiezza e solidità di strumenti a dir poco impressionante.
Anche se tale formula non rappresenta il propagatore di Schrodinger è lo stesso utile per risolvere
problemi concernenti lequazione stazionaria di Schrodinger come tenteremo di illustrare in questa
sezione. Una bella panoramica su questo tipo di problemi la si può trovare su Kac, Integration
in Function Spaces and Some of Its Applications, Scuola Normale Superiore, Pisa.
4.1 LIntegrale Funzionale
Cominciamo dunque dal problema di trovare il propagatore per lequazione di Schrodinger
_
_
_
ihtu(t, x) =
h
2
2
u(0, x) = (x),
Introdotta lhamiltoniana quantistica
1 =
h
2
2
d
2
dx
2
+V (x) =:
h
2
+ V,
dove lultima espressione a destra è la notazione operatoriale di quella a sinistra, la soluzione u può
essere scritta come
u(t) = e
i
h
t;
= e
i
h
t
_
h
2
2
+V
_
.
36
Al momento la notazione e
i
h
t
_
h
2
2
+V
_
è solo virtuale, poiche sembra abbastanza problematico
estendere la formula
e
z
=
n
z
n
n!
,
al caso in questione, producendo
e
i
h
t;
=
n
(
i
h
t)
n
n!
1
n
, (4.1)
a causa delle dicoltà che abbiamo già incontrato con loperatore /H nella meccanica classica.
Per risolvere ecacemente questo tipo di problemi è stata sviluppata la teoria dei semigruppi di
operatori, che però esula totalmente dai nostri scopi. Vedremo invece di arontare la situazione
pi` u o meno con le mani. Per fare questo separiamo i due operatori della somma e consideriamo
separatamente le due equazioni
ihu
(t) =
h
2
u(t), ihu
(t) = V u(t), (4.2)

dove V è loperatore di moltiplicazione per la funzione V , cioè [V ](x) := V (x)(x). La seconda
delle (4.2) è facilmente risolvibile, essendo di fatto una semplice equazione ordinaria lineare. Infatti,
per esteso è
ihtu(t, x) = V (x)u(t, x), = u(t, x) = u(0, x)e
i
h
tV (x)
= (x)e
i
h
tV (x)
.
Operatorialmente possiamo scrivere che
_
e
i
h
tV
_
(x) = e
i
h
tV (x)
(x), e
i
h
tV
= e
i
h
tV (x)
.
La prima è molto meno elementare, essendo di fatto unequazione a derivate parziali
ihtu(t, x) =
h
2
2
xxu(t, x).
Non è possibile ripetere il tipo di calcoli fatti con loscillatore armonico. Fisicamente si capisce il
perche. Lequazione di Schrodinger precedente corrisponde al caso sico del potenziale nullo, dunque
totale assenza di forze. Per cui lenergia non avrà autovalori diversi da 0 perche non ci saranno valori
dellenergia fuori dallunico valore 0. Questo può essere vericato direttamente provando a trovare
gli autovalori di 10 =
h
2
2
d
2
dx
2
. Di fatto 10 dovrebbe agire attraverso un propagatore unitario
puro, cioè del tipo e
i
(cosa che per esempio non è nel caso delloscillatore armonico come mostra
la formula di Mehler). A questo proposito e per evitare confusioni chiariamo un punto: in ogni caso
loperatore e
i
h
t;
è unitario, cioè conserva la norma in X. Tuttavia può modicare puntualmente
in estensione lo stato. Ci aspettiamo invece che nel caso di 10 la modica puntuale sia puramente
unitaria. Per dedurre la forma esplicita di kt(x, y) in questo caso ricicliamo le considerazioni
seguenti alla formula di Mehler, ed in particolare quella per cui, almeno per t piccolo si dovrebbe
avere
kt(x, y)
1
i2ht
e
i
h
,(q)
.
Nel nostro caso V = 0 dunque /(q) =
_
t
0
1
2
q(s)
2
ds
1
2
_
xy
t
_
2
t =
(xy)
2
2t
, cos` che si dovrebbe
avere
kt(x, y)
1
i2ht
e
i
h
(xy)
2
2t
Sorprendente o meno che sia, questa formula è esatta! Precisamente risulta che
e
i
h
t;
0
(x) :=
_
R
kt(x, y)(y) dy =
_
R
(y)
1
i2ht
e
i
h
(xy)
2
2t
dy
risolve la prima delle (4.2) per tutti i tempi t (e non solo per t piccolo). Una verica formale può
essere fatta direttamente facendo le derivate del caso.
37
Ora passiamo al vero e proprio problema, determinare il propagatore corrispondente allhamiltoniana
generica H(q, p) =
1
2m
p
2
+V (q), cioè determinare una funzione kt(x, y) tale che
e
i
h
t;
(x) =
_
R
kt(x, y)(y) dy. (4.3)
Nel nostro caso 1 = 10 +V dunque
e
i
h
t;
= e
(
i
h
t;
0)+(
i
h
tV )
= e
A+B
,
dove A =
i
h
10 e B =
i
h
tV . A questo punto il gioco sembra fatto: usando la ben nota formula
e
A+B
= e
A
e
B
si trova che
e
i
h
t;
= e
i
h
t;
0
e
i
h
tV
, e
i
h
t;
(x) =
_
R
1
i2ht
e
i
h
(xy)
2
2t
e
i
h
V (y)
(y) dy. (4.4)
Ma qui avviene un colpo di scena: la funzione scritta a destra nella (4.4) non risolve aatto
lequazione di Schrodinger! Il fatto è che la formula e
A+B
= e
A
e
B
è, nel nostro caso, falsa. In-
fatti una condizione sotto la quale la si può dimostrare (almeno formalmente e rigorosamente sotto
debite ipotesi su A e B) vale se [A, B] = 0. A noi non interessa dimostrarla poichè il nostro A è del
tipo P
2
e B è del tipo V (Q). Siccome P e Q non commutano ci sarà da aspettarsi che nemmeno
P
2
e V (Q) lo facciano
(17)
. Tutto da buttare? Fortunatamente no grazie al bel
Teorema 4.1 (Formula di Lie) Siano A e B operatori limitati. Allora
e
A+B
= lim
n
_
e
1
n
A
e
1
n
B
_
n
. (4.5)
Dim. Per denizione
e
A+B
=
n=0
1
n!
(A+B)
n
,
e la serie converge nella norma operatoriale.
Applichiamo la formula di Lie al nostro caso. Abbiamo che
e
i
h
t;
= lim
n
_
e
i
h
t
n
;
0
e
i
h
t
n
V
_
n
= lim
n
e
i
h
t
n
;
0
e
i
h
t
n
V
e
i
h
t
n
;
0
e
i
h
t
n
V
. (4.6)
Osserviamo anzitutto che
_
e
i
h
t
n
;
0
e
i
h
t
n
V
_
(x) =
1
_
i2h
t
n
_
R
e
i
h
n
t
(xy)
2
2
_
e
i
h
t
n
V
_
(y) dy
=
1
_
i2h
t
n
_
R
e
i
h
n
t
(xy)
2
2
e
i
h
t
n
V (y)
(y) dy
=
1
_
i2h
t
n
_
R
e
i
h
_
n
t
(xy)
2
2

t
n
V (y)
_
(y) dy
=
_
R
t
n
(x, y)(y) dy,
dove abbiamo posto
s(x, y) =
1
2his
e
i
h
_
1
2
(xy)
2
s
sV (y)
_
.
17
Salvo casi banali ovviamente, ad esempio V (x) fosse costante.
38
Allora
_
e
i
h
t
n
;
0
e
i
h
t
n
V
_
e
i
h
t
n
;
0
e
i
h
t
n
V
__
(x) =
_
R
t
n
(x, z)
_
e
i
h
t
n
;
0
e
i
h
t
n
V
_
(z) dz
=
_
R
t
n
(x, z)
_
R
t
n
(z, y)(y) dy dz
=
_
RR
t
n
(x, z) t
n
(z, y)(y) dz dy,
Iterando la procedura e tenendo conto della (4.6) abbiamo che
e
i
h
t;
(x) = lim
n
_
R
n
t
n
(x, x1) t
n
(x1, x2) t
n
(xn1, y)(y) dx1 dx2 dxn1 dy. (4.7)
da cui
kt(x, y) = lim
n
_
R
n
t
n
(x, x1) t
n
(x1, x2) t
n
(xn1, y) dx1 dx2 dxn1. (4.8)
Apparentemente la questione sarebbe risolta, senonchè la rappresentazione (4.8) è dicile da in-
terpretare. Sarebbe opportuno avere una formula indipendente dal limite in n. A tal proposito
osserviamo che, ponendo x0 = x, xn = y abbiamo
n
k=1
t
n
(x
k1
, x
k
) =
1
_
(2hi)
n
_
t
n
_
n
n
k=1
e
i
h
(
1
2
n
t
(x
k
x
k1
)
2
t
n
V (x
k
))
=
1
_
(2hi)
n
_
t
n
_
n
e
i
h
_
1
2
k
[
n
t
(x
k
x
k1
)
2
t
n
V (x
k
)]
_
Lidea è ora di interpretare i punti x
k
come le posizioni di una traiettoria a diversi istanti. Sup-
poniamo cioè che q(t) sia una traiettoria che parte al tempo t = 0 dal punto xn = y ed arriva al
tempo t nel punto xn = x e che agli istanti t
k
= k
t
n
si trovi nella posizione x
k
, cioè:
q(0) = y, q(t) = x, q(t
k
) = x
k
, t
k
= k
t
n
.
Allora
1
2
k
_
n
t
(x
k
x
k1
)
2
t
n
V (x
k
)
_
=
k
_
1
2
(q(t
k
) q(t
k1
))
2
t
k
t
k1
(t
k
t
k1
)V (q(t
k
))
_
.
Ora
q(t
k
) q(t
k1
) = q(
k
)(t
k
t
k1
),
per cui
1
2
k
_
n
t
(x
k
x
k1
)
2
t
n
V (x
k
)
_
=
k
_
1
2
q(
k
)
2
(t
k
t
k1
) (t
k
t
k1
)V (q(t
k
))
_
_
t
0
1
2
q(s)
2
V (q(s)) ds
= /(q) .
Si intuisce che adesso siamo vicini alla generalizzazione (nonche ad una migliore comprensione) della
(3.17). In un certo senso potremmo scrivere
kt(x, y) = lim
n+
_
R
n
1
_
(2hi)
n
_
t
n
_
n
e
i
h
k
_
1
2
(q(t
k
)q(t
k1
))
2
t
k
t
k1
(t
k
t
k1
)V (q(t
k
))
_
dq(t1) dq(tn)
(4.9)
39
Lidea è adesso quella di interpretare la (4.9) come un integrale sullo spazio di tutte le traiettorie
congiungenti y ad x (cioè tali che q(0) = y, q(t) = x) cioè
kt(x, y) =
_
C(t,x,y)
e
i
h
,(q)
dT(q), (4.10)
dove
((t, x, y) è lo spazio di tutte le traiettorie q tali che q(0) = y e q(t) = x;
dT(q) è una misura sullo spazio dei cammini: empiricamente
dT(q) = lim
n
1
_
(2hi)
n
_
t
n
_
n
n
k=1
d(q(t
k
)). (4.11)
La formula (4.10), dovuta a Feynman, prende il nome di formula di Feynman. Il suo signicato è
molto profondo. Il propagatore esprime come viene propagata la probabilità di trovare la parti-
cella in una determinata posizione (ovverosia lo stato ). Questa ampiezza di probabilità per una
transizione dalla posizione y a quella x si ottiene attraverso una media di contributi elementari che
sono legati allazione (la stessa che, minimizzata, caratterizza le traiettorie di moto). Per ulteriori
approfondimenti si rimanda al libro di Feynman & Hibbs
18
Il problema matematico (e non è solo una questione formale) è che purtroppo nessuno dei termini
che compongono la (4.10), vale a dire lesponenziale dellazione, la costante moltiplicativa e la misura
prodotto, ha senso! In altre parole il limite esiste ma non possiamo identicarlo con una misura
sullo spazio delle traiettorie. La questione è matematicamente tanto dicile che ad oggi esistono
solo tentativi molto parziali di dare senso rigoroso alla (4.10).
4.1.1 Il problema del rigore della formula di Feynman
Il problema di dare senso alla formula di Feynman (4.10) è molto complesso. Anzitutto perche
lintegrale (4.10) è fatto su uno spazio innito dimensionale (lo spazio delle traiettorie) ed in secondo
luogo per la particolarità della funzione integranda q e
i
h
,(q)
. La teoria generale dellintegrazione,
detta teoria della misura, oggi ben compresa, si è sviluppata a partire dallinizio del 900 ad opera
principalmente di Lebesgue e Borel, ed è un sicuro ambiente di lavoro per trattare problemi come
quello della formula di Feynman. Tuttavia negli spazi innito dimensionali, come prevedibile, la
teoria è molto pi` u complessa che negli spazi nito dimensionali. Uno dei fatti semplici ed interessanti
è che se immaginiamo il prodotto
n
k=1
d(q(t
k
)) come un prodotto di misure di Lebesgue (le dx
k
per intenderci), tutto ciò ha un senso ntanto che n è nito, ma quando n è innito il prodotto perde
completamente di signicato. Il motivo intrinseco è legato alle proprietà caratteristiche della misura
di Lebesgue, che sono di essere invariante per traslazioni ed assegnare misura nita ai limitati.
Cè un semplice ed ecace argomento che ci illustra il problema. Consideriamo la generalizzazione
di R
n
, R
:=
_
(xn)
n=1
:
n
[xn[
2
< +
_
. Non è dicile dimostrare che R
è uno spazio
vettoriale completo con la norma |x| :=
_
n
xn. Tale spazio è anche uno spazio di Hilbert
munito del prodotto scalare (x, y) =
n
xnyn, dove ovviamente x = (xn), y = (yn). Si può
addirittura dimostrare che R
è il prototipo del generico spazio di Hilbert separabile (cioè munito

di un sottoinsieme numerabile denso), nel senso che ogni spazio di Hilbert separabile è isometrico
ad R
. Ora il fatto è che non esiste su R
alcuna misura denita sui boreliani

(19)
di R
che sia
invariante per traslazione ed assegni misura nita ai limitati.
Infatti: supponiamo che tale misura esista. Consideriamo le palle B
k
di R
centrate nei punti

e
k
:= (
kn
)n (
kn
è il simbolo di Kronecker) e di raggio
1
2
. Si vede immediatamente che tali palle
sono tutte disgiunte tra loro e che si possono traslare luna nellaltra e sono tutte traslate della palla
B0 := B(0,
1
2
[, nel senso che B
k
= B0 +e
k
. Ma allora
_
_
k
B
k
_
=
k
(B
k
) =
k
(B0 +e
k
) =
k
(B0).
18
Od anche al libretto di Feynman, QED, dove la formula non viene mai esplicitamente introdotta, ma si
cela dietro tutto ci` o che viene detto.
19
Con boreliani intendiamo la algebra generata dagli aperti di R
.
40
Poiche
k
B
k
B(0, 2] deve essere
_
k
B
k
_
< +; ma allora (B0) = 0.
`
E ora facile concludere
che la misura di ogni palla deve essere nulla, e quindi 0.
Oltre al problema di denire la misura dT la formula di Feynman presenta anche un impor-
tante inconveniente sulla funzione integranda che, essendo questa un esponenziale immaginario,
non aiuta molto, almeno a priori, nella convergenza dellintegrale. La cosa interessante è che an-
che se è un esponenziale immaginario, è di tipo molto particolare. Infatti consideriamo il caso in
cui V = 0. Lesponenziale è di tipo e
i
2
e questo ricorda gli integrali di Fresnel
_
R
e
ix
2
dx che sono
convergenti come integrali generalizzati (ma non come integrali alla Lebesgue). In qualche senso
questo apre una possibile strada, seguita in anni recenti da Albeverio ed altri, per tentare di dare
un senso alla (4.10).
4.2 La Formula di FeynmanKac
Abbiamo detto che il principale problema della formula di Feynman è quello della sua denizione
rigorosa. Intorno agli anni 50 del secolo scorso, Kac riusc` a dare un senso perfettamente rigoroso
ad una formula simile che, in luogo del propagatore di Schrodinger, rappresenta il propagatore
per la soluzione dellequazione del calore (o di diusione). Sebbene lequazione del calore e quella
di Schrodinger e quella del calore siano profondamente diverse, la formula di FeynmanKac ha
permesso di risolvere rigorosamente una quantità impressionante di problemi anche per la meccanica
quantistica. Mostreremo uno di questi in seguito.
Il punto di partenza è la seguente, forse banale, osservazione. Immaginiamo che u sia soluzione
dellequazione di Schrodinger
ihtu(t, x) =
h
2
2
ed osserviamo che se, formalmente, pensiamo il tempo t come immaginario puro, cioè se introdu-
ciamo la funzione v(t, x) := u(iht, x) allora
tv(t, x) = ihtu(iht, x) =
h
2
2
xxu(iht, x) V (x)u(iht, x) =
h
2
2
xxv(t, x) V (x)v(t, x),
cioè v è soluzione del problema
_
_
_
tv(t, x) =
h
2
2
xxv(t, x) V (x)v(t, x) =: (v(t, x),
v(0, x) = (x).
(4.12)
Questa è una ben nota equazione della sica matematica, precisamente quella che governa la diu-
sione del calore in un corpo: v(t, x) è la temperatura al tempo t nel punto x; v(0, x) è la temperatura
iniziale. Eettuando la sostituzione t iht nelle formule scritte sopra si trova che il propagatore
diventa
s(x, y) =
1
2h
2
s
e
1
2
(xy)
2
h
2
s
sV (y)
.
ed il nucleo (4.10) assume la forma
gt(x, y) =
_
C(t;x,y)
e
_
t
0
1
2 h
2
q(s)
2
+V (q(s)) ds
dl(q), (4.13)
dove ((t; x, y) resta denito come sopra e
dl(q) = lim
n
1
_
_
2 h
2
t
n
_
n
n
k=1
d(q(t
k
)).
Anche in questo caso nessuno dei tre termini che compongono lespressione (4.13), vale a dire le-
sponenziale, la costante di normalizzazione e la misura prodotto, ha senso singolarmente preso, ma,
in questo caso, il prodotto dei tre invece ha senso! Lidea è di riscrivere la (4.13) come
gt(x, y) =
_
C(t;x,y)
e
_
t
0
V (q(s)) ds
dW
t
x,y
(q), (4.14)
41
dove ora
dW
t
x,y
(q) =
1
_
_
2 h
2
t
n
_
n
e
1
2 h
2
_
t
0
q(s)
2
ds

0<s<t
d(q(s)).
Osservato che
_
t
0
q(s)
2
ds =
_
t
0
q(s)q(s) ds =
__
d
2
d
2
_
q, q
_
L
2
(0,t)
.
Per cui possiamo riscrivere la misura W
t
x,x
come
dW
t
x,y
(q) =
1
_
_
2 ht
1
2
((D
2
)q,q)
0<s<t
d(q(s)), (4.15)
dove si è posto D =
1
h
d
dx
. Cos` scritta W
t
x,y
non può fare a meno di ricordarci la misura gaussiana
A(0, ) su R denita attraverso la formula
A(0, )(A) =
1
2
_
A
e
1
2
1
x
2
dx.
La sua generalizzazione ddimensionale è
A(0, )(A) =
1
_
(2)
d
det()
_
A
e
1
2
1
xx
dx1 dx
d
.
La matrice si dice matrice di covarianza. La W
t
x,y
sembrerebbe cos` come una sorta di misura
gaussiana innito dimensionale di covarianza (D
2
)
1
. Il problema è che la (4.15) contiene troppe
quantità innite, per cui bisogna trovare un metodo per denire la W
t
x,y
. Il primo che è riuscito
rigorosamente a costruire questa misura è stato Wiener nel 1923 e la misura cos` costruita prende
il nome appunto di misura di Wiener e la formula (4.14) è la celebre formula di FeynmanKac.
Poichè la costruzione della misura di Wiener si basa su idee siche accenniamo nella prossima
sezione alla sua costruzione. Le applicazioni della formula di Feynman-Kac alla meccanica quanti-
stica riprenderanno nella sezione successiva alla prossima.
4.3 La misura di Wiener
Questa è una lunga storia. Nel corso dell800 un botanico, tale R. Brown, si mise ad osservare
sperimentalmente il moto di particelle pesanti in sospensione in un uido riportando delle compli-
catissime traiettorie irregolari seguite dalle particelle. Al tempo non erano ancora noti esempi di
funzioni particolarmente irregolari, come le funzioni costruite da Weierstrass che non ammettono
derivata in nessuno dei punti del loro dominio di denizione, cos` che il modello delle equazioni
dierenziali non sembrava un buon modello per descrivere tale moto e, al tempo stesso, non si
disponeva ancora di modelli alternativi matematicamente.
Allinizio del 900 lattenzione su questo fenomeno sico, che nel frattempo aveva assunto il nome
di moto browniano, sotto linusso delle nuove idee statistiche introdotte in sica da Boltzmann,
venne posta da parecchi sici ed i matematici cominciarono ad interessarsene. Da un lato Einstein
& Smoluchowskii avevano pensato ad un modello in cui le particelle si muovessero come in una
passeggiata aleatoria, introducendo il concetto di probabilità di transizione, cioè le probabilità che
una particella si muova da un punto ad unaltro dello spazio. Tale probabilità, in accordo con il
Teorema del Limite Centrale, veniva calcolata attraverso la formula
Prob. (q(t) A [ q(s) = x) =
1
_
2
2
(t s)
_
A
e
(yx)
2
2
2
(ts)
dy =:
_
A
pts(x, y) dy, (4.16)
dove
2
è il cosidetto coeciente di diusione. Mettendo assieme i risultati di Einstein & Smolu-
chowskii con dati sperimentali e statistica rudimentale, il sico Perrin riusc` per la prima volta a
42
determinare il numero di Avogadro, scoperta che gli valse il premio Nobel
(20)
nel 1926.
Daltro canto lo stesso Perrin fu il primo ad osservare che un buon modello del moto browniano
andava ricercato nelle mostruose funzioni introdotte da Weierstrass. Questosservazione colp` pro-
fondamente Wiener il quale, estendendo la costruzione di Weierstrass, riusc` a denire un modello
statistico in cui si consideravano simultaneamente tutte le traiettorie continue, pensandole come
funzione sia del tempo che di una variabile aleatoria, cioè q = q(t, ), che fosse coerente con le
probabilità di transizione (4.16), e che inoltre facesse emergere come con probabilità 1 le traiettorie
dovessero essere estremamente irregolari. Di fatto questo equivaleva ad aver pensato lo spazio delle
traiettorie continue come uno spazio di probabilità munito di una misura di probabilità che succes-
sivamente avrebbe assunto il nome di misura di Wiener. La costruzione di Wiener venne ripresa
pi` u volte e generalizzata via via a probabilità di transizione pi` u generali di quelle di Einstein &
Smoluchovskii. Con lavvento della moderna teoria della misura negli anni 30 del 900 Kolmogorov
riusc` a fondare su basi rigorose il calcolo delle probabilità. A Kolmogorov è dovuta la costruzione
pi` u generale e semplice di una misura tipo quella di Wiener, ed è a questa costruzione che ora
accenneremo.
Il punto di partenza sono appunto le densità di probabilità di transizione, cioè le funzioni p
h
(x, y),
h > 0. Queste funzioni sono densità di probabilità probabilità poiche
_
R
p
h
(x, y)dy = 1. (4.18)
Questequazione non dice altro che la probabilità di andare da qualche parte in un tempo h partendo
dal punto x è 1. Osserviamo che questa ipotesi è strettamente connessa al fenomeno della diusione
del calore ed è perfettamente in accordo con lidea che il calore si propaga a velocità innita.
Attraverso le probabilità di transizione p
h
(x, y) possiamo calcolare la probabilità di eventi com-
plessi. Di particolare importanza sono gli eventi del seguente tipo: linsieme delle traiettorie che
giungono ad un certo istante t2 > 0 in I2 passando al tempo 0 < t1 < t2 per I1, partendo al tempo
0 < t0 < t1 in x. Si tratta di fare una specie di slalom fra le porte I1 ed I2.
`
E naturale pensare che
anzitutto dovremo andare da x ad un generico x1 I1 in un tempo t1 t0: la probabilità di arrivare
vicino ad x1 a meno di un piccolo errore dx1 sarà pt
1
t
0
(x, x1) dx1. Poi da x1 dovremo andare ad
un certo x2 I2 in un tempo t2 t1, e la probabilità di nire vicino ad x2 a meno dellerrore dx2
sarà pt
2
t
1
(x1, x2) dx2. Il problema è: come si combinano le due probabilità ? Lidea è quella di
pensare i due passi come eventi indipendenti tra loro, per cui
pt
1
t
0
(x, x1) dx1 pt
2
t
1
(x1, x2) dx2,
sarà la probabilità totale. Non ci resta ora che sommare su tutti gli x1 I1 e tutti gli x2 I2 per
ottenere
Prob. (q(t1) I1, q(t2) I2 [ q(t0) = x) =
_
I
1
pt
1
t
0
(x, x1) dx1
_
I
2
pt
2
t
1
(x1, x2) dx2.
Iterando la procedura consideriamo levento che una particella parta ad un determinato istante t0
in x e ad istanti via via successivi t0 < t1 < t2 < . . . < tn si trovi rispettivamente in I1, I2, . . . , In.
La probabilità corrispondente sarà
Prob. (q(t1) I1, . . . , q(tn) In [ q(t0) = x)
=
_
I
1
pt
1
t
0
(x, x1) dx1
_
I
2
pt
2
t
1
(x1, x2) dx2
_
In
ptnt
n1
(xn1, xn) dxn.
(4.19)
20
Lidea è approssimativamente la seguente. Dalla (4.16) è possibile dimostrare che lo spostamento medio
di una particella è nullo e che lo spostamento quadratico medio è direttamente proporzionale allintervallo
di tempo in cui si considera lo spostamento. In formule:
Media su q di (q(t
) q(t)) = 0, Media su q di (q(t
) q(t))
2
= (t
t). (4.17)
Prendendo ora un gran numero di traiettorie sperimentali si pu` o calcolare il valore (t
t). Se t
t è noto
questo calcolo determina . Ora contiene essenzialmente il numero di Avogadro per la formula =
kT
3a
,
essendo k la costante di Boltzmann, T la temperatura assoluta, a il raggio delle molecole ed il coeciente
di viscosit` a. Il legame col numero di Avogadro è dato dalla formula k =
R
N
, R costante dei gas perfetti ed
N numero di Avogadro.
43
Si pone a questo punto un problema naturale di coerenza. Infatti potremmo dire che per t0 < s < t
deve essere
Prob. (q(t) I [ q(t0) = x) = Prob. (q(t) I, q(s) R [ q(t) = x), I R,
ovvero che
_
I
ptt
0
(x, y) dy =
_
R
pst
0
(x, y) dy
_
I
pts(y, z) dz =
_
I
_
R
pst
0
(x, y)pts(y, z) dy dz,
da cui ricaviamo lequazione di EinsteinSmoluchovskii
p
a+b
(x, y) =
_
R
pa(x, z)p
b
(z, y) dz. (4.20)
`
E semplice vericare che eettivamente questa equazione è vericata dalle probabilità di transizione
della (4.16). Inne, che è quanto ci interessa, possiamo calcolare la probabilità che la traiettoria
parta al tempo 0 in y ed arrivi al tempo t in x passando attraverso le porte I1, I2, . . . In ai tempi
0 < t1 < t2 < . . . < tn < t. Avremo
Prob. |q : q(t1) I1, . . . , q(tn) In [q(0) = y, q(t) = x
=
_
I
1
In
pt
1
(y, x1) pt
2
t
1
(x1, x2) pttn
(xn, x) dx1dx2 . . . dxn.
(4.21)
Un insieme di traiettorie del tipo di quelli introdotti nella (4.21) viene detto cilindro e lo in-
dicheremo nel seguito con (t1, . . . , tn; I1 In). Ad essere corretti ed onesti bisogna osser-
vare che la (4.21) non è una vera e propria probabilità poiche se, come ci si dovrebbe aspettare,
Prob. |q : q(t1) R, . . . , q(tn) R [q(0) = y, q(t) = x = 1, invece tale probabilità vale esatta-
mente pt(y, x). Ad ogni modo il risultato seguente permette di aermare lo stesso che esiste eetti-
vamente una misura sullo spazio delle traiettorie (funzioni continue) che assegna ai cilindri il valore
(4.21). Il punto chiave è la (4.20).
Teorema 4.2 (Kolmogorov) Se |p
h
(, ) : h > 0 è una famiglia di densità di probabilità soddis-
facenti alle equazioni (4.18) & (4.20) allora esiste una misura su
((t; x, y) = |q C([0, t]; R) : q(0) = y, q(t) = x ,
la cui misura sui cilindri è assegnata dalla formula (4.21). Nel caso di p
h
assegnato dalla formula
(4.16), tale misura verrà indicata con il simbolo W
t
x,y
.
Ribadiamo il fatto che W
t
x,y
non è una misura di probabilità nel senso che W
t
x,y
(((t; x, y)) non è
uguale ad 1. In eetti vale
W
t
x,y
(((t; x, y)) = pt(x, y).
Per ottenere una misura di probabilità basta quindi normalizzare W
t
x,y
. Questo punto è secondario e
quindi terremo la misura W
t
x,y
cos` come labbiamo denita. Per concludere è importante osservare
che la costruzione fatta si basa solamente sulle equazioni (4.18) & (4.20).
A questo è possibile dare un senso rigoroso alla (4.14) sotto un minimo di ipotesi per V . Per
esempio: se V è inferiormente limitata e continua allora la (4.14) è denita come lintegrale su
((t, x, y) del funzionale q e
_
t
0
V (q(s)) ds
rispetto alla misura W
t
x,y
.
`
E opportuno qui precisare che la costruzione di Kolmogorov è valida senza variazioni tecniche
quando le traiettorie sono a valori vettoriali (cioè q(t) R
n
). Ciò rende applicabile immediatamente
la (4.14) al caso sico interessante del potenziale coulombiano.
44
4.4 Applicazioni della formula di FeynmanKac alla MQ
La (4.14) è certo una bellissima e suggestiva formula, ma sembra dicile vedere come applicarla
a problemi concreti, sopratutto perche si tratta di un integrale innito dimensionale, dunque poco
maneggevole per i calcoli. Tuttavia si è mostrato in numerosissime applicazioni che tale formula
permette di studiare moltissime proprietà dei sistemi quantistici. Per unillustrazione matematica
di tali applicazioni rimandiamo al già citato libro di Kac, mentre per le applicazioni pi` u siche,
anche se in genere quasi prive di rigore, il libro di Feynman & Hibbs è il riferimento pi` u indicato.
In questa sezione ci limiteremo ad un paio di esempi abbordabili ed interessanti e, comunque,
per nulla banali.
4.4.1 La legge di Planck
Una delle prime leggi della sica atomica è stata introdotta da Planck quando ancora la meccanica
quantistica non era stata formalizzata. Tale legge aerma che i livelli ammissibili dellenergia sono
un certo insieme discreto |En
nN
, En < En+1 e, per n grande, En 2hn. Il nostro scopo in
questo paragrafo è dedurre questa legge sotto alcune minime ipotesi.
Ricordiamo anzitutto che i valori ammissibili dellenergia sono gli autovalori n dellhamiltoniana
quantistica, cioè le soluzioni dellequazione stazionaria di Schrodinger che qui riportiamo per con-
venienza
h
2
2m
(x) +V (x)(x) = (x). (4.22)

Si può dimostrare che se limxV (x) = + e V è limitato dal basso, allora la (4.22) ammette
una successione n di autovalori con corrispondente base ortonormale |n in X = L
2
(R). Un
caso particolare di ciò labbiamo visto nel caso delloscillatore armonico, dove V (x) =
1
2
x
2
.
Assumiamo per semplicità che m = 1. Ripetendo i conti fatti per il propagatore di Schrodinger
nel caso del calore, tenuto conto che (n = nn, abbiamo
v(t, x) =
_
R
(y)
_
n
e
nt
n(x)n(y)
_
dy =:
_
R
(y)gt(x, y) dy,
e, dalla formula di FeynmanKac (4.14), si ha
n
e
nt
n(x)n(y) = gt(x, y) =
_
C(t;x,y)
e
_
t
0
V (q(s)) ds
dW
t
x,y
(q). (4.23)
In particolare, ponendo y = x abbiamo che
n
e
nt
n(x)
2
=
_
C(t;x,x)
e
_
t
0
V (q(s)) ds
dW
t
x,x
(q),
ed, integrando in x e tenuto conto che |n| = 1, abbiamo inne la
n
e
nt
=
_
R
__
C(t;x,x)
e
_
t
0
V (q(s)) ds
dW
t
x,x
(q)
_
dx. (4.24)
Supponiamo che t 0.
`
E naturale attendersi che
e
_
t
0
V (q(s)) ds
e
tV (x)
,
e quindi che
_
R
__
C(t;x,x)
e
_
t
0
V (q(s)) ds
dW
t
x,x
(q)
_
dx
_
R
e
tV (x)
W
t
x,x
(((t; x, x)) dx
=
_
R
e
tV (x)
pt(x, x) dx
=
_
R
e
tV (x)
1
2h
2
t
dx,
45
cos` che la (4.24) può essere riscritta, per t 0 come
n
e
nt
2h
2
t
_
R
e
tV (x)
dx =
1
2h
_
R
2
e
t
_
p
2
2
+V (x)
_
dp dx. (4.25)
Introduciamo ora la variabile darea A =
p
2
2
+ V (x) e guardiamo lintegrale a destra nella (4.25)
per fette rispetto alla variabile A:
_
R
2
e
t
_
p
2
2
+V (x)
_
dp dx =
_
+
A
min
e
t
dA(),
dove A() = Area
_
p
2
2
+V (x)
_
. Anche il primo membro della (4.25) può essere scritto come
un integrale, introducendo la misura di conteggio
N() := (n : n < ) ,
per cui
n
e
nt
=
_
+
1
e
t
dN().
Morale
_
+
1
e
t
dN()
1
2h
_
+
A
min
e
t
dA(). (4.26)
Da questa sarebbe ora possibile mostrare che
N()
1
2h
A(), +. (4.27)
da cui,
A(n) 2hn, n +.
Naturalmente la dimostrazione rigorosa della (4.25) e della (4.27) sono un po delicate tecni-
camente, ma i passaggi precedenti sono lo scheletro della dimostrazione di quanto annunciato
nellintroduzione.
5 Il problema della QFT
Siamo nalmente giunti al punto in cui è possibile parlare del problema di quantizzare un campo.
Per mostrare lessenza del problema considereremo il caso pi` u semplice. Sebbene un po idealizzato
permette di illustrare bene le notevoli dicoltà che si incontrano nella teoria, senza complicare
troppo gli aspetti formali.
Cominciamo col concetto di campo. Fisicamente lorigine del termine viene dallelettrodinamica
e campo sta per campo elettromagnetico. La teoria della relatività ha poi mostrato limportanza
del campo gravitazionale nella teoria geometrica dello spaziotempo
(21)
. Lente matematico adatto
a descrivere un campo è una funzione = (t, x) R
n
con x R
3
, dove t è il tempo ed x è la
variabile spaziale. Per incorporare la teoria della relatività generale bisognerebbe parlare di campo
su una varietà dierenziale (lo spaziotempo), e questo introduce ulteriori complicazioni.
In ogni caso, ciò di cui disponiamo sono le equazioni di evoluzione del campo, che sono lanalogo
delle equazioni di Newton per le particelle nella Meccanica Classica. Lanalogia è eettivamente
questa perche si possono introdurre delle equazioni di Hamilton ed il formalismo dei principi vari-
azionali per descrivere la dinamica. Su questa base, una volta introdotte le equazioni di Newton,
calcoleremo lhamiltoniana ed introdurremo il formalismo di Heisenberg per la descrizione classica
del sistema. Quindi passeremo il formalismo di Heisenberg dentro alla macchina della quantizzazione
già vista nel passaggio dalla Meccanica Classica a quella Quantistica. Nel fare ciò dovremo introdurre
21
Rimandiamo a Landau & Lifshiz, Teoria dei Campi, Editori Riuniti, per tutto quanto concerne dette
teorie
46
le nuove parentesi di Poisson, le coordinate canoniche (la Q e la P) e le regole di commutazione
fra queste. Quindi per analogia con la meccanica quantistica introdurremo lo spazio degli stati
come spazio di funzioni integrabili, le osservabili ed in particolare procederemo alla quantizzazione
delle coordinate canoniche e dellhamiltoniana. Questoperazione risulterà però molto complessa e
parecchie novità interverranno. In particolare il tentativo di quantizzare lhamiltoniana mostrerà
che questa è sempre innita ed una procedura apposita (detta rinormalizzazione) permetterà di
capire come modicare lhamiltoniana anchè questa ritorni ad avere un senso.
Se la meccanica quantistica è dicile perche comporta un livello di analisi su spazi innito di-
mensionali, la teoria quantistica dei campi è ancora pi` u dicile, stando in rapporto alla MQ tanto
quanto questa è in rapporto con la MC. Volendo mettere in parallelo i principali aspetti potremmo
riassumere il tutto con la tabella
MC MQ QFT
Spazio degli stati R
2
L
2
C
(R
2
) L
2
_
L
2
C
(R
2
)
_
(misura su R
2
) (misura su spazi di dim. )
Osservabili funzioni operatori operatori
H funz. scalare op. dierenziale op. dierenziale
(ellittico, 1-dimensionale) (ellittico, dim.)
Necessita rinormalizzazione
Evoluzione stati eq. Hamilton eq. Schrodinger eq. Schrodinger
(PDE, 1-dim) (PDE, dim)
Traiettorie ODE SDE SPDE
dove ODE sta per equazioni dierenziali ordinarie, SDE per equazioni dierenziali stocastiche e
SPDE per equazioni dierenziali stocastiche a derivate parziali.
5.1 Equazione di KleinGordon
Cominciamo con le equazioni di Newton per il campo elettromagnetico. Qui considereremo il caso
di un campo = (t, x) : R R R, dove t indica il tempo ed x lo spazio. In realtà un campo
sarebbe un vettore di funzioni del tipo precedente, ma per non complicare le cose noi ne prenderemo
una sola. Lequazione che descrive levoluzione del campo si chiama equazione di KleinGordon ed
è
( +m
2
)(t, x) := tt(t, x) xx(t, x) +m
2
(t, x) = f((t, x)). (5.1)
Il simbolo prende il nome di DAlembertiano od operatore di DAlembert. Lequazione (5.1) è una
riduzione e semplicazione delle equazioni di Maxwell per il campo elettromagnetico. Per brevità e
per evitare confusione con le derivate che introdurremo a breve scriveremo tt = tt e cos` via.
Il primo passo consiste nel riscrivere lequazione (5.1) sotto forma di sistema Hamiltoniano, esat-
tamente come abbiamo fatto a suo tempo con le equazioni di Newton. Come allora abbiamo:
_
_
_
t(t, x) = (t, x),
t(t, x) =
_
xx(t, x) +m
2
(t, x) +f((t, x))
_
(5.2)
Si tratta di trovare ora lHamiltoniana H (classica), cioè una funzione delle coordinate (, ) tale
che il sistema (5.2) si possa scrivere come
_
t =
H,
t =
H.
(5.3)
In questo caso la faccenda si complica perchè bisogna dare un senso alle derivate parziali
H
ed
H. Anzitutto osserviamo che lo spazio delle fasi sarà uno spazio di funzioni, sulle quali richie-
deremo tutte le proprietà che via via diverranno necessarie per svolgere i calcoli e dare senso alle
varie espressioni che interverranno
(22)
. Chiamiamo S questo spazio. Sarà conveniente assumere una
qualche struttura su S e quella pi` u comoda è sicuramente quella hilbertiana, cos` che considereremo
S := L
2
R
(R).
22
Anche se vedremo che, nostro malgrado, il concetto di funzione ordinaria non sar` a suciente. . .
47
Lhamiltoniana classica H dovrà allora essere una funzione H : D(H) S S R. Una funzione
come la H, cioè una funzione da uno spazio funzionale a valori numerici, viene detta funzionale
(23)
.
Il dominio di H potrebbe essere messo a posteriori di modo che eettivamente valga il sistema (5.3).
Un dominio comodo, come vedremo, è D(H) = C
c
(R) C
c
(R).
Proviamo ora a vedere se riusciamo ad indovinare la forma della derivata H. Inspirandoci
allazione della meccanica classica poniamo
H(, ) =
1
2
_
R
(x)
2
dx +V (),
dove per il momento V è un non meglio precisato funzionale di . Vediamo che la scelta è giusta:
H(, +) H(, ) =
_
R
dx +o()
2
,
per ogni funzione . La parte
_
R
dx è lineare nellincremento per cui è naturale vedere
loperazione di integrale come un prodotto scalare e porre a vettore rappresentativo di
H()
esattamente . La determinazione del funzionale V è un po pi` u complicata ma oramai dovremmo
aver capito. Ad esempio un termine del tipo
m
2
2
_
R
2
dx, (5.4)
produrrà come derivata m
2
. Riettiamo un istante: la trasformazione m
2
può essere vista
come g , dove g(z) = m
2
z. Per costruire il funzionale che ha questa trasformazione per
derivata (cioè la sua primitiva) noi prendiamo la funzione G(z) =
m
2
2
z
2
, cioè G tale che G
= g ed
il funzionale è dato da _
R
G((x)) dx.
Questo modo complicato di scrivere la posizione (5.4) ci permette di vedere facilmente il potenziale
del termine f , che sarà
_
R
F((x)) dx,
essendo F una primitiva della funzione numerica f. La verica è immediata perchè
_
R
F (( +)(x)) dx
_
R
F((x)) dx =
_
R
f((x))(x) dx +o().
Ci rimane il termine xx. Ricordando sempre lazione classica sarà naturale porre, come
primitiva di questa trasformazione,

1
2
_
R
x(x)
2
dx.
La verica è la solita formula dintegrazione per parti:
1
2
_
R
( +)x(x)
2
dx
1
2
_
R
x(x)
2
dx =
_
R
x(x)x(x) dx =
_
R
xx(x)(x) dx.
In conclusione lhamiltoniana è il funzionale:
H(, ) =
1
2
_
R
_
(x)
2
+x(x)
2
+m
2
(x)
2
)
_
dx +
_
R
F((x)) dx. (5.5)
Passiamo ora al calcolo dellazione. Per questa abbiamo bisogno della lagrangiana. Va detto che
in realtà esiste una relazione precisa fra hamiltoniana e lagrangiana, una formula che permette
23
Unesempio labbiamo gi` a incontrato con lazione della meccanica classica.
48
di calcolarne una nota laltra. Tale operazione si chiama trasformata di Legendre. Qui andremo a
cercare direttamente la lagrangiana. Essa sarà della forma
/() =
_
R
2
/((t, x), t(t, x), x(t, x))dtdx,
dove / : R R R R sarà la lagrangiana. Come troviamo questa funzione? Imponendo che
/ = 0 corrisponda allequazione di KleinGordon. Per non creare confusione chiamiamo con

, , le variabili indipendenti di /. Ad esempio /
è la derivata parziale di / rispetto alla prima

variabile. Dunque, trascurando i termini di ordine superiore al primo nellincremento ,
/ =
_
R
2
/( +, t +t, x +x) dtdx
_
R
2
/(, t, x) dtdx
=
_
R
2
/
+/()t +/
()x dtdx (per parti)

=
_
R
2
|/
t/ x/
dtdx.
Bisogna notare che la notazione / sta per:
/((t, x), t(t, x), x(t, x)),
avendo omesso largomento per mantenere le notazioni il pi` u possibile compatte. Allo stesso modo
si deve considerare /
. Ora A contiene termini trascurabili in se e solo se

/
t/ x/
= 0,
da cui si vede lequazione di KleinGordon se
/(, t, x) =
m
2
2

2
+F()
1
2
2
t
+
1
2
2
x
. (5.6)
Il caso in cui f 0 viene detto di campo libero. In questa sezione tratteremo solo questo caso. La
teoria di campo libero è ben compresa. Tuttavia, come suggerisce la denominazione della teoria
stessa, riguarda lassenza di interazioni, per cui non rappresenta un caso sicamente realistico. La
teoria generale è ancora ad oggi largamente incompleta. Esiste una teoria P()2 completa, che
signica quando f è un polinomio in nel caso di dimensione spaziale 1 (2 sta per una dimensione
temporale ed una spaziale). Ci sono alcuni casi particolari in dimensione 3 = 1 + 2 ma non cè una
teoria generale, cos` come in dimensione 4 = 1 + 3, che è il caso sicamente interessante.
Per concludere osserviamo che lhamiltoniana di campo libero è in un certo senso equivalente ad un
sistema innito di oscillatori armonici accoppiati (e questo è un rudimentale sintomo di aumentata
complessità). Euristicamente si tratta di sostituire alla somma integrale una somma discreta:
H(, ) =
1
2
_
R
_
(x)
2
+x(x)
2
+m
2
(x)
2
)
_
dx
1
2
2
n
+m
2
2
n
+ (n n1)
2
.
Il termine n n1 rappresenta appunto il termine dinterazione.
5.2 Parentesi di Poisson
Abbiamo visto quanta parte abbiano avuto le parentesi di Poisson nel passaggio dalla meccanica
classica a quella quantistica. Per mantenere il parallelo introduciamo anche qui le parentesi di Pois-
son classiche per la teoria dei campi. La procedura formale è la stessa della meccanica classica. Un
osservabile f è una funzione sullo spazio delle fasi a valori numerici, un funzionale cioè, non lineare
in genere. Esempio notevole è appunto lhamiltoniana (5.5). In generale levoluzione dellosservabile
f è regolata dalla formula
f
t
(, ) = f((t), (t)),
49
ove (t) = (t, ), (t) = (t, ) è la soluzione del sistema (5.2) tale che (0) = , (0) = .
Lequazione dierenziale è pertanto
tf
t
=
f

(t) +
f

(t) = |f, H
t
,
dove
|f, g :=
g.
Questa formula andrebbe presa con una certa cautela perchè le varie derivate parziali sono in realtà
da intendere come operatori lineari ed il prodotto scalare da intendere come azione del funzionale
a sinistra del segno sul vettore a destra del segno. Ora linterpretazione può sembrare chiara nel
caso della formula scritta sopra dove compaiono termini del tipo
f

(t).
Qui (t) è il vettore e
f il funzionale. Viceversa nella denizione generale non è pi` u chiaro quale

dei due termini debba rappresentare il vettore e quale loperatore. La cosa è di una certa importanza
poichè a noi interessa calcolare le parentesi delle osservabili pi` u interessanti, le coordinate. Vediamo
come in questo caso la questione venga risolta.
Anzitutto dobbiamo notare che, a dierenza del caso della MC dove avevamo una sola osservabile
Q ed una sola P, denite come Q(q, p) = q, P(q, p) = p rispettivamente, qui di osservabili
classiche ce ne siano innite per la Q e per la P. In eetti una coordinata tipo Q è ora tutto un
campo = (x). Possiamo quindi considerare, al variare di x R le osservabili
x
(, ) = (x).
Analogamente porremo
y
(, ) = (y).
Calcoliamo (almeno formalmente) |
x
,
y
al variare di x ed y. Abbiamo bisogno delle derivate
parziali. Ad esempio calcoliamole per
x
. Ovviamente, poichè
x
non dipende da è
x
= 0.
Inoltre
x
( +, )
x
(, ) = (x).
Essendo questa lineare nellincremento avremo che
x
(, ) = (x).
Analogamente
y
0,
y
(, ) = (y).
Come facciamo ora a calcolare
y
? Dobbiamo rappresentare una delle due derivate
parziali con una funzione lasciando agire laltra come operatore. Per esempio andiamo a rapp-
resentare
y
(è del tutto indierente quale delle due, dato che sono identiche formalmente).
Possiamo scrivere
y
(, ) = (y) =
_
R
(z)y(z) dz,
dove y è la celebre funzione di Dirac centrata in y, cioè una funzione tale che
y(z) 0, y(z) = 0, z ,= y,
_
R
f(z)y(z) dz = f(y) per ogni f.
Una simile funzione è dicile da immaginare ed in eetti non esiste. A meno di cambiare il con-
cetto di funzione e passare a quello di funzione generalizzata, o distribuzione. Noi non ci occuperemo
di questo problema tecnico che porta a rivoluzionare non poco le possibilità del calcolo.
Dunque, ammettendo che
y
(, ) = y,
avremo che
|
x
,
y
(, ) =
x
(, ) y = y(x) = 0(x y).
50
Vediamo qui che luso delle funzioni come la diventa problematico poichè il risultato della parentesi
di Poisson sarebbe 0 se x ,= y mentre varrebbe per x = y!
Come ho detto sopra, questo problema in realtà è sormontabile facilmente generalizzando legger-
mente la denizione delle osservabili
x
e
y
. Per fare ciò osserviamo che
x
(, ) = (x) = x, ),
azione del funzionale x sul campo (per denizione: x, ) := (x)). Tale x non è una funzione,
ma può essere sostituita da una funzione con supporto molto concentrato intorno al punto x.
Poniamo dunque, per analogia
(, ) := , ) =
_
R
(x)(x) dx.
Similmente
(, ) = , ) =
_
R
(x)(x) dx.
`
E chiaro allora che
(, ) = ,
(, ) = ,
e come sempre
0,
0.
`
E ora semplice calcolare la parentesi di Poisson:
|
= , ). (5.7)
5.3 Rappresentazione di Schrodinger
Siamo ora pronti per quantizzare la teoria sopra esposta. Come abbiamo visto nella MQ abbiamo
bisogno dei seguenti ingredienti:
i) di uno spazio degli stati X ottenuto come L
2
C
(S): uno stato rappresenta una distribuzione di
probabilità (una volta normalizzato) ed esprime la probabilità di trovare il campo in certe
congurazioni piuttosto che altre; gli operatori simmetrici rappresentano le osservabili reali;
ii) di parentesi quantistiche: determinano le regole di commutazione fra le osservabili; avendole
già ricavate nella MQ possiamo già n dora denirle come
ih[F, G] = FGGF;
iii) di coordinate canoniche quantizzate: sono una famiglia di coordinate tipo Q ed una di tipo
P, rispettivamente |
e |
, di cui venga data la regola di commutazione basata sulla

(5.7);
iv) di unhamiltoniana quantizzata.
Si tratta di un programma estremamente complesso che, a parte il secondo punto (invariato rispetto
alla MQ), richiederà parecchie modiche rispetto allo schema che formalmente generalizza quello
della MQ. In questo senso lapproccio di Feynmann dimostra la sua essenziale bellezza descrivendo
tutta la teoria tramite un solo ente matematico, una misura sullo spazio dei cammini.
5.3.1 Spazio degli stati: misure gaussiane in dimensione innita
La prima dicoltà ci appare quando poniamo, formalmente
X = L
2
C
(S) =
_
: S C :
_
S
[()[
2
d <
_
.
Il problema è: che cosa rappresenta d? Abbiamo già incontrato nel paragrafo 4.1.1 questo tipo di
problema, cioè denire una misura su uno spazio innito dimensionale. La generalizzazione naturale
dalla MQ, per cui d è la generalizzazione ad innite dimensioni della misura di Lebesgue, non è
percorribile come visto nel paragrafo 4.1.1. Come fare allora?
Andando a rileggere i risultati per loscillatore armonico ci si accorge che lo spazio X della MQ può
essere equivalentemente riscritto in un modo che, come vedremo tra poco, può essere trasportato
anche al nostro caso. In quel caso, infatti, abbiamo costruito una base ortonormale di autostati per
lhamiltoniana
n(x) =
1
2
n
h
n
n!
pn(x)0(x) =: qn(x)0(x),
51
dove 0(x) = ( h)
1/4
e
x
2
2 h
. Base signica che
(n, m)
L
2
C
(R)
= nm, (, n)
L
2
C
(R)
= 0, n, = = 0.
Ora: osservato che
(n, m)
L
2
C
(R)
=
_
R
qn(x)qm(x)0(x)
2
dx = (qn, qm)
L
2
C
(R;)
dove (dx) = 0(x)
2
dx =
1
h
e
x
2
2 h
dx è una misura gaussiana.
autostati che, per costruzione, avevano la forma
n(x) = (n!)
1/2
n(
2x)0(x),
dove n(x) è un polinomio, precisamente lnesimo polinomio di Hermite e 0(x) è una gaussiana,
precisamente
0(x) =
1/4
e
1
2
x
2
.
Lo spazio degli stati era L
2
C
(R) e si può osservare che
n L
2
C
(R) (n!)
1/2
n L
2
C
(R; 0(x)
2
dx),
dove naturalmente
L
2
C
(R; 0(x)
2
dx) :=
_
p : R C [
_
R
[p(x)[
2
0(x)
2
dx =
_
R
[p(x)[
2
A
_
0,
1
2
_
(dx) <
_
.
Introduciamo qui una notazione molto importante: chiamiamo monomio di Wick
24
il polinomio
: x
n
: := (n!)
1/2
n(
2x).
Questa notazione è particolarmente importante perchè dire che il sistema di autostati |nn forma
una base ortonormale per L
2
C
(R) signica dire che | : x
n
: n forma una base ortonormale per
L
2
C
_
R; A
_
0,
1
2
__
. In particolare,
_
R
: x
n
: : x
m
: A
_
0,
1
2
_
(dx) = nm,
ove qui nm sta per la delta di Kronecker, cioè nm = 0 se n ,= m altrimenti vale 1.
Questo discorso ha messo in chiara evidenza la struttura gaussiana già presente nella MQ. Si
potrebbe andare molto oltre, come ad esempio interpretando il signicato dei monomi di Wick.
Da un punto di vista puramente matematico questi possono essere visti come il risultato del pro-
cedimento di ortogonalizzazione di GramSchmidt applicato alla successione standard di polinomi
|1, x, x
2
, . . . , x
n
, . . . nello spazio euclideo L
2
C
_
R; A
_
0,
1
2
__
, interpretazione certo non molto ap-
petibile al sico. Linterpretazione sica la si ricava quando si mette in relazione loperatore Q con
gli operatori di creazione A
e distruzione A
. Precisamente, ricordiamo che

Q =
1
2
(A
+A
).
Questa equazione si ottiene invertendo la denizione di A
e A
. Ora Q è un operatore (operatore

di moltiplicazione) per cui Q
n
ha un senso ben preciso e, in virt` u dellequazione precedente può,
essere scritto come
Q
n
= 2
n/2
(A
+A
)
n
.
Poichè sappiamo che A
e A
non commutano, precisamente [A
, A
] = I, non possiamo conclud-

ere che
Q
n
= 2
n/2
n
k=0
_
n
k
_
(A
)
k
(A
)
nk
,
24
La denizione che di solito viene data di monomio di Wick dierisce da quella che riporto qui per un
coeciente moltiplicativo
52
come conseguenza dello sviluppo del binomio. Cosa rappresenta allora la quantità a destra, sviluppo
formale del binomio come se A
e A
commutassero ? Ebbene questa è proprio il monomio di Wick

: Q
n
:
25
, a meno di un coeciente moltiplicativo. Precisamente
Teorema 5.1
_
n!
2
n
: Q
n
:= 2
n/2
n
k=0
_
n
k
_
(A
)
k
(A
)
nk
, (5.8)
Il fatto è che lespressione (5.8) assume grandissima importanza nella teoria quantistica dei campi. Il
motivo è il seguente. In quel caso la denizione analoga di Q
n
contiene quantità innite ed in genere
è mal posta. Questo fatto impedirebbe la costruzione della teoria stessa. Senonchè si è osservato
che lanaloga denizione (5.8) ha straordinariamente senso. Cioè mentre nella MQ unespressione
del tipo Q
n
ha sempre senso cos` come : Q
n
:, quando si passa a quantizzare un campo la prima
quantità è innita mentre la seconda no. Per questo le quantità naturali da considerare non sono
della forma Q
n
ma : Q
n
:. La cosa per il momento può apparire molto nebulosa tanto che sia Q
n
che : Q
n
: sono polinomi di grado n in Q per cui non è chiaro per quale ragione uno debba essere
innito e laltro no! Questa procedura di sostituzione di quantità innite attraverso la sottrazione
di altre quantità innte a produrre quantità nite viene chiamata rinormalizzazione. Nella MQ la
rinormalizzazione non è necessaria quanto invece lo è nella teoria quantistica dei campi. Poichè
grande ruolo è giocato dalla formula (5.8) si è soliti denire : Q
n
: proprio come il secondo membro
della (5.8)
26
.
Torniamo inne alla questione di come denire la misura gaussiana A(0, C). La digressione sulla
MQ, o meglio sulla rivisitazione del caso delloscillatore armonico, ci porta inevitabilmente a tentare
di procedere per analogia. Se riettiamo però sulla costruzione di quel caso, vediamo che ciò di
cui abbiamo bisogno è la struttura di autostati dellhamiltoniana quantizzata. Il guaio è che per
quantizzare lhamiltoniana avremo bisogno della struttura dello spazio X già denita. Volendo
evitare circoli viziosi, accetteremo per il momento la struttura gaussiana non avendo ancora denito
la matrice
27
di covarianza C.
5.3.2 Regole di commutazione
Deniamo le parentesi
ih[F, G] := FGGF,
per F e G operatori lineari su X. Questa denizione è conforme alle regole introdotte in MQ dove
abbiamo provato che una parentesi [, ] soddisfacente lassioma 3.7 è necessariamente della forma
detta sopra (teorema di Dirac 3.8). Tale deduzione è puramente algebrica e prescinde dallo spazio
degli stati X soggiacente, per cui la riterremo senzaltro valida anche nel contesto dei campi. Un
minimo dattenzione richiede invece la quantizzazione della condizione (5.7).
Anzitutto ad ogni avremo associato operatori
su X. Il modo naturale di tradurre la

(5.7) è attraverso lequazione
ih[
] = , )I, , . (5.9)
A dire il vero bisognerebbe anche analizzare che succede quando cerchiamo di commutare un oper-
atore
con
. La risposta ci viene immediatamente dalle parentesi di Poisson classiche poichè

in tal caso
|
= 0,
perchè
0 per quanto visto sopra. Dunque oltre alla (5.9) avremo le

[
] = 0, [
] = 0, , . (5.10)
Del resto linterpretazione è chiara: se vogliamo misurare la posizione od il momento in due punti
diversi dello spazio le due misurazioni non interferiscono fra loro (questo è quanto aerma la
25
Cioè quelloperatore che si ottiene sostituendo ad x loperatore Q nel polinomio algebrico : x
n
:.
26
Questo introduce la costante moltiplicativa, di cui abbiamo detto in precedenza, come fattore di
(n!)
1/2
n(
2Q).
27
Matrice innito dimensionale.
53
(5.10)); se si vuole misurare simultaneamente una posizione ed un momento allora non si ha in-
terferenza se si misurano le due quantità simutaneamente in due punti diversi altrimenti si ha
interferenza. Questultima interpretazione corrisponde in realtà ai campi
x
e
y
dove lequazione
(5.9) suonerebbe come
ih[
x
,
y
] = xyI.
Tuttavia questa notazione, abbiamo detto in precedenza, è pericolosa ed ambigua. Possiamo lo
stesso avere una bella interpretazione della (5.9) come segue:
non interferiscono fra loro

se e sono spazialmente separate, cioè se i supporti
28
di e sono disgiunti.
Chiariamo questo punto con un esempio. Non potendo parlare di
x
e
y
possiamo pensare
sostituire
x
con un operatore del tipo
A
dove A R è un intorno di x. Ciò corrisponde al
mediare i valori del campo in un intorno di x, per cui lesito di
A
su uno stato coinvolgerà
solo i valori di (z) con vicino ad x (a meno dellerrore denito dallintorno A). Analogamente
sostituiamo
y
con
B
, ove B è un intorno di y. Se x ,= y possiamo sempre trovare A e B
disgiunti per cui A, B) = [AB[ = [[ = 0. Da questo segue che
A
e
B
commutano. In un
certo senso questo rende dellintuizione che, se per misurare
A
ci servono i valori del campo in A,
A
, dopo la misurazione, avrà perturbato solo quei valori e niente altro. Analogamente per
B
,
per cui è chiaro che nessuno dei due debba inuire sui risultati dellaltro, donde la commutatività.
5.3.3 Operatori di moltiplicazione e derivazione
Siamo ora giunti alla quantizzazione dei campi
29
di operatori
. Quantizzare signica denire
come operatore su X (lineare e simmetrico). Nella MQ avevamo posto [Q](x) = x(x). Lidea
potrebbe quindi essere di porre [
]() = () dopodichè, però, non avremmo una funzione

scalare. In eetti dobbiamo ragionare sempre col caso ideale =
(cioè lo stato è esattamente il

campo

). Allora deve risultare che
[
x
]() =
_
0 se ,=

(x) se =

_
= (x)
() = , x)
().
Da questa ci è immediato porre
[
]() = , )(). (5.11)

`
E immediato vericare che
cos` denita è unosservabile reale:

(
1, 2)
X
=
_
S
, )1()2()(d)
=
_
S
1(), )2()(d),
essendo , ) R.
Passiamo a
. Come già nel paragrafo 3.8.2 serviamoci dellequazione di commutazione (5.9). Per
evitare di portarci dietro anche h , poniamo questa costante uguale ad 1. La regola di commutazione,
scritta per esteso, assume la forma
i
_
, )[
]()
[, )()]()
_
= , )(). (5.12)
Loperatore
rappresenta il momento per cui è naturale porre (a generalizzazione della P quan-

tistica e seguendo le linee di ragionamento di sopra)
[
]() = i
(), ) . (5.13)
28
Per supporto di una funzione regolare sintende la parte del dominio dove la funzione è diversa da 0.
29
Diciamo campi perchè siamo partiti dallapplicazione tipo x
x
.
54
Verichiamo che
soddisfa la (5.12). Dobbiamo procurarci
[, )()]. Basta tener presente

che
è unusuale derivata e soddisfa le regole del prodotto:
[, )()] = i
[, )()] , )
= i () +, )
(), ) =
= i, )() i, )
(), )
= i, )() i
]().
Quando andiamo a vericare se
denito dalla (5.13) è simmetrico in X ci troviamo di fronte ad

un nuovo problema. Impostando il calcolo
_
1, 2
_
X
=
_
S
[
1]()2()(d)
= i
_
S
1(), ) 2()(d)
= i
__
S
1()2()(d),
_
Il problema sorge quando cerchiamo di fare lintegrazione per parti, di modo da spostare la derivata
su 2. In eetti dobbiamo tenere conto del fatto che (d) non è lordinaria misura di Lebesgue,
invariante per traslazioni (su cui il principio dellintegrazione per parti è basato). Tuttavia la situ-
azione non è poi cos` drammatica. Visto che = A(0, C) possiamo pernsare che
(d) = e
1
2
C
1
,)
d.
Ribadiamo che a regola questa non è corretta perchè d non ha senso. Noi ora procederemo formal-
mente, come se avesse senso e dedurremo una formula dintegrazione per parti dipendente solo da
e prenderemo questa formula per buona. Dunque:
_
S
1()2()e
1
2
C
1
,)
d =
=
_
S
1()
_
2()e
1
2
C
1
,)
_
d
=
_
S
1()
_
2 2()C
1
_
e
1
2
C
1
,)
d
=
_
S
1()
_
2() 2()C
1
_
(d).
Moltiplicando scalarmente per arriviamo allidentità
_
S
1(), ) 2()(d) =
_
S
1()(
2(), ) 2()C
1
, ))(d). (5.14)
Reintroducendo la i ed loperatore
possiamo interpretare la precedente nella seguente scrittura:

_
1, 2
_
X
=
_
1,
2 +i
C
1
2
_
X
. (5.15)
Per reintrodurre
C
1
abbiamo usato il fatto che C

1
è a sua volta simmetrico rispetto al prodotto
, ), per cui
C
1
, )2() = , C
1
)2() =
C
1
2().
55
Dunque quando spostiamo
da una parte allaltra del prodotto scalare compare un termine ex-

tra sommato a
. Dunque
non è formalmente simmetrico. Per renderlo tale basta modicarne

la denizione nel seguente modo: poniamo
[
]() = i
(), ) +
i
2
[
C
1
](). (5.16)
Se notiamo, per analogia col gradiente classico, che il primo addendo nella (5.16) è i moltiplicato
per la derivata direzionale nella direzione porremo
() =
(), ) .
Da questa otteniamo
= i
+
i
2
C
1
.
La formula di integrazione per parti (5.14) si riscrive come:
_
S
1()2()(d) =
_
S
1()
_
2()
C
1
2()
_
(d),
e la (5.15) come
(i
1, 2)
X
=
_
1, i
2 +i
C
1
2
_
X
.
A questo punto la simmetria di
può essere determinata algebricamente in modo semplice:

_
1, 2
_
X
= (i
1, 2)
X
+
_
i
2
C
1
1, 2
_
X
=
_
1, i
2 +i
C
1
2
_
X
+
i
2
_
1,
C
1
2
_
X
(perchè
C
1
è simmetrico)
=
_
1, i
2 +
i
2
C
1
2
_
X
=
_
1,
2
_
X
.
Avendo cambiato la denizione di
da
i
a i
+
i
2
C
1
,
ed avendo provato che
i [
, i
] = , )I,
può sorgere in dubbio che questa equazione non sia pi` u soddisfatta da
cos` come denito dalla

(5.16)
30
. In realtà
è costituito da due parti: una che soddisfa la condizione ed una che commuta
con
(il cui commutatore è quindi zero e non inuisce pertanto sul risultato nale). Precisamente
i
_
= i
_
, i
+i
_
,
i
2
_
= , )I + 0.
5.3.4 Quantizzazione di H: rinormalizzazione
Questo è il problema pi` u delicato. Lidea semplicemente di sostituire le espressioni dei campi
x
e
y
(che, come abbiamo detto abbiamo in realtà solo sotto la forma
) porta ad alcuni
problemi. Innanzi tutto abbiamo un problema tecnico: la presenza del termine x nellespressione
dellhamiltoniana. La trasformata di Fourier è lo strumento che permette di risolvere elegantemente
la questione.
30
Aprendo lo spiraglio per uno spaventoso circolo vizioso nel quale modichiamo
anchè valga una

certa condizione e di l` a poco lo rimodichiamo perchè nel primo modo non vale una seconda etc. . .
56
Teorema 5.2 Data una funzione si pone
() :=
1
2
_
R
e
ix
(x)dx.
si dice trasformata di Fourier di e gode delle seguenti proprietà:

(i) (derivazione)

x() = i
();
(ii) (isometria)
_
(x)(x)dx =
_

()
()d.
(iii) (inversione)
(x) =
1
2
_
e
ix
()d,
Applicando due volte la proprietà (i) in particolare si ottiene che
xx() =
2
().
Per cui il termine dellhamiltoniana contenente il gradiente può essere riscritto (applicando un
integrazione per parti e la proprietà (ii)) come
_

2
x
=
_
xx =
_

xx
=
_

2
()d.
Applicando ancora la (ii) ai termini quadratici restanti otteniamo lhamiltoniana nelle coordinate
coniugate:
H(, ) =
1
2
_

()
2
+ (
2
+m
2
)
()
2
d.
In questa forma ci ricorda ancor di pi` u lhamiltoniana di oscillatore armonico, nel senso che, dis-
cretizzando lintegrale
H(, )
1
2
n
(
2
n
+(n)
2
2
n
), (5.17)
ove ()
2
=
2
+ m
2
. Lhamiltoniana discretizzata ci appare ora come lhamiltoniana di un os-
cillatore armonico innito dimensionale. La sua troncatura nito dimensionale, che viene detta
troncatura ultravioletta
31
, può essere studiata esattamente come per loscillatore armonico unidi-
mensionale. Poichè nelle coordinate coniugate sparisce linterazione lanalisi è molto semplice. Per
esempio gli autostati dellhamiltoniana sono dati da prodotti dei corrispondenti autostati di quella
unidimensionale. Sarebbe interessante mettere in chiaro la struttura delle soluzioni di questo caso
per mettere in chiaro in modo semplice lorigine dei problemi del caso innito dimensionale, ma
richiederebbe ulteriore spazio e tempo. . .
Torniamo al nostro problema: quantizzare lhamitoniana (5.17). Dobbiamo procurarci le versioni
quantistiche di

() e

(). Procediamo in modo formale:
() =
1
2
_
e
ix
x
dx,
ed unanaloga denizione per

(). Ovviamente sappiamo che
x
e
y
non esistono, per cui
bisognerebbe generalizzare la precedente denizione. Per risolvere questo problema si percorre, pi` u
o meno, la strada delineata in precedenza che ci ha portato alla denizione di
. Osserviamo
ad esempio che
[
()]() =
1
2
_
e
ix
[
x
]()dx =

()(),
31
Il verbo deriva dallinterpretazione di n, o meglio di . Questa è infatti una frequenza, nel senso che,
dalla formula dinversione si pu` o leggere come ricostruita a partire dalle funzioni trigonometriche e
ix
,
per le quali ha signicato di frequenza, attraverso una combinazione lineare generalizzata (lintegrale) con
pesi dati da

().
57
per cui si potrebbe porre
[
]() =
, )().
Qualcosa di simile può essere fatto anche per

. Qui, come ho detto, continueremo con

()
e

(
). Allora

()
2
è un certo operatore e cos` pure lo è

()
2
. Lhamiltoniana quantistica
diventerebbe allora una sorta di combinazione lineare generalizzata di questi operatori, cioè
10 :=
1
2
_

()
2
+()
2
()
2
d. (5.18)
Lindice 0 sta a ricordarci che il termine dinterazione f è nullo. La (5.18) è per il momento una
denizione puramente formale
32
; immaginiamo che il problema degli operatori

() e

() possa
essere arontato come abbiamo visto sopra.
Procediamo con lanalogia con loscillatore armonico. Il prossimo passo è lintroduzione degli
operatori di creazione e distruzione attraverso i quali introdurre gli autostati. Questo operatori
vengono fuori dalla fattorizzazione dellhamiltoniana quantistica ed è esattamente quello che ora
cercheremo di fare. Riscriviamo lhamiltoniana come
10 =
_
()
1
2
_
1
()
()
2
+()
()
2
_
d.
Gli operatori (o meglio campi di operatori) di creazione e distruzione sono deniti dalla fattoriz-
zazione formale del termine in parentesi quadre nellespressione precedente, vale a dire, rispettiva-
mente
A
() :=
1
2
_
_
()
()
i
_
()
()
_
,
A
() :=
1
2
_
_
()
() +
i
_
()
()
_
,
(5.19)
Come già nel caso quantistico cè daspettarsi che A
() e A
() non commutino. Come in quel caso

per calcolare le regole di commutazione per gli operatori di creazione e distruzione abbiamo bisogno
delle stesse per le coordinate generalizzate coniugate. Queste possono essere facilmente ricavate se
si osserva che
i
_
(),

(
=
1
2
_ _
e
i(x+
y)
i [
x
,
y
] dxdy
=
1
2
_ _
e
i(x+
y)
(x y)I dxdy
=
1
2
_
e
i(
)x
dx I
= (
)I.
Ovviamente sul penultimo integrale abbiamo chiuso un occhio! Come al solito è facile immaginare
quale forma assumerà il commutatore. Ora siamo in grado si calcolare il commutatore degli operatori
di distruzione e creazione:
_
A
(), A
= (
)I.
Usando questequazione lhamiltoniana è presto riscritta in termini di operatori di creazione e dis-
truzione:
10 =
_
()
_
A
()A
() +A
()A
()
d. (5.20)
Abbiamo cos` ottenuto lequivalente della (3.12). La fattorizzazione (5.18) ci permette di scoprire
la singolarità dellhamiltoniana 10, singolarità che impone una cruciale modica allhamiltoniana
stessa.
32
In eetti niente dentro lintegrale è denito rigorosamente
58
Prendiamo spunto dallutilità degli operatori di creazione e distruzione (ed dal loro signicato
sico). Loperatore di distruzione è stato introdotto col signicato di distruggere energia. In parti-
colare abbiamo trovato uno stato 0 tale che
A
0 = 0.
Lo stato 0 è quello di energia minore, tutti gli altri stati fondamentali (cioè autostati dellhamiltoniana)
vengono ottenuti iterando loperatore di creazione su 0. Cambiando poi lo spazio X da L
2
C
(R; dx)
a L
2
C
(R; A(0, 1/2)) lo stato 0 diventa particolarmente semplice, essendo la funzione identicamente
uguale ad 1. Siccome in innite dimensioni, cioè nel caso della teoria dei campi, solo lambito gaus-
siano ha senso, lo stato fontamentale 0 deve essere la funzione 0() 1. Ora è facile vericare
che con le nostre posizioni eettivamente si ha
A
()1 = 0, .
Ma ecco che,
101 =
_
()
_
A
()A
()1 +A
()A
()1
d =
_
()d = +!
Da questo fatto segue ad esempio che
_
(x)
2
dx = +,
quindi un pezzo consistente dellhamiltoniana è innito, e cos` pure lo sono i termini rimanenti. Per
vedere questo fatto osserviamo che, invertendo le equazioni,
() =
1
_
2()
_
A
() +A
()
. (5.21)
Per cui
()
2
=
1
2()
(A
() +A
())
2
=
1
2()
_
A
()
2
+A
()
2
+A
()A
() +A
()A
()
.
Applicando alla funzione 0 1 si trova
()
2
1() =
1
2()
_
[A
()
2
1]() + 1
.
Integriamo su ed usiamo lisometria della trasformata di Fourier:
_
(x)
2
dx =
_

()
2
d =
_

()
2
0()d
=
_
1
2()
A
()
2
0()d +
1
2
_
d
()
.
Lultimo integrale è di fatto innito mentre si può vedere che il primo non lo è. Sono queste le
famose singolarità da cui nasce la misteriosa operazione della rinormalizzazione.
In eetti il fatto è che si può mostrare che lespressione
10 =
_
()
_
A
()A
() +A
()A
()
d = 2
_
()A
()A
()d
ottenuta sostituendo al termine A
()A
() il termine A
()A
(), cioè spostando a destra gli

operatori di distruzione ed a sinistra quelli di creazione, è eettivamente ben posta. Per lo meno non
da problemi sullo stato fondamentale 0, che costituisce il fatto pi` u importante, visto che tutti gli
stati si dovrebbero ottenere da questo con creazioni successive. Pi
in generale è possibile mostrare

che di qualsiasi espressione contenente prodotti di operatori di creazione con operatori di distruzione
è priva di senso a meno di non avere spostato tutti gli operatori di distruzione a destra e quelli di
creazione, corrispondentemente, a sinistra.
59
Abbiamo già incontrato questoperazione nel paragrafo 5.3.1. Attualizzando quel contesto pren-
diamo la (5.21) e supponiamo di voler introdurre la potenza nesima di

(). A regola avremmo
()
n
=
1
(2()
n/2
_
A
() +A
()
_
n
.
Sviluppando la potenza, dato che A
() e A
() non commutano vengono a crearsi termini misti.

Con un conto del tutto simile a quello visto sopra per il quadrato, sebbene molto pi` u laborioso,
otteniamo senzaltro che _

()
n
0()d = +.
Tuttavia loperatore che formalmente si ottiene se gli operatori di creazione e distruzione commu-
tassero,
2
n/2
k
_
n
k
_
A
()
k
A
()
nk
,
risulta ben posto. In analogia con la (5.8) il secondo membro della precedente si chiama monomio
di Wick e si denota con :

()
n
:. Si può vedere che, per n pari (ciò è dovuto alla trasformata di
Fourier) risulta
_
:

()
n
: d =
_
: (x)
n
: dx.
In particolare loperazione di sostituzione dellhamiltoniana quantistica 10 con quella rinormalizzata
10 equivale a sostituire lhamiltoniana classica con lhamiltoniana
H0(, ) =
1
2
_
: (x)
2
+x(x)
2
+m
2
(x)
2
: dx.
Il metodo della rinormalizzazione apre quindi la strada per la quantizzazione dei sistemi non lin-
eari, cioè quelli in cui è presente interazione, traducibile nella presenza di una non linearità f
nellequazione di KleinGordon (5.1). Se ad esempio f((t, x)) = (t, x)
4
si opera sostituendo

()
4
con :

()
4
. Rendere matematicamente rigorosa la teoria è un compito molto dicile e tecnico che
qui non ho nemmeno sorato. La quantizzazione del campo libero invece non è tutto sommato molto
diversa dalla serie di operazioni che ho descritto in questultimo paragrafo, anche se, ovviamente,
molta cautela è richiesta nel maneggiare gli inniti.

Un'Introduzione Alla Teoria Quantistica Dei Campi

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Un'Introduzione Alla Teoria Quantistica Dei Campi

Uploaded by

Copyright:

Available Formats

UnIntroduzione alla Teoria Quantistica dei

q(t) +qV ( q(t))

q(t) +qV ( q(t))q(t)dt = 0,

q(t) +qV ( q(t)) = 0, t [t0, t1].

[det J(Tt)(q, p)[dqdp = [[,

= q qpp +qqp p p qqp pqq p.

e lordine `e importante. Questo fra laltro mette

= [F, G]. (3.4)

= ((F I)(F I), ) = 0,

(x) sia, a meno di costanti, il

Ft = [Ft, 1] = [F, 1]t

= 0 e quindi = (, ) dove [(, )[ = 1 per cui si pu`o scrivere

come operatore di distruzione,

= 0, che vuol dire = 0.

] = iI, [1osc, A] = iA.

(x) = 4(2 hx +)(x), da cui

(t) = V u(t), (4.2)

`e il prototipo del generico spazio di Hilbert separabile (cio`e munito

. Ora il fatto `e che non esiste su R

alcuna misura denita sui boreliani

centrate nei punti

) q(t)) = 0, Media su q di (q(t

(x) +V (x)(x) = (x). (4.22)

/ = 0 corrisponda allequazione di KleinGordon. Per non creare confusione chiamiamo con

`e la derivata parziale di / rispetto alla prima

()x dtdx (per parti)

. Ora A contiene termini trascurabili in se e solo se

f il funzionale. Viceversa nella denizione generale non `e pi` u chiaro quale

, di cui venga data la regola di commutazione basata sulla

. Precisamente, ricordiamo che

. Ora Q `e un operatore (operatore

non commutano, precisamente [A

] = I, non possiamo conclud-

commutassero ? Ebbene questa `e proprio il monomio di Wick

su X. Il modo naturale di tradurre la

. La risposta ci viene immediatamente dalle parentesi di Poisson classiche poich`e

0 per quanto visto sopra. Dunque oltre alla (5.9) avremo le

non interferiscono fra loro

. Quantizzare signica denire

]() = () dopodich`e, per`o, non avremmo una funzione

(cio`e lo stato `e esattamente il

]() = , )(). (5.11)

cos` denita `e unosservabile reale:

rappresenta il momento per cui `e naturale porre (a generalizzazione della P quan-

soddisfa la (5.12). Dobbiamo procurarci

[, )()]. Basta tener presente

`e unusuale derivata e soddisfa le regole del prodotto:

denito dalla (5.13) `e simmetrico in X ci troviamo di fronte ad

possiamo interpretare la precedente nella seguente scrittura:

abbiamo usato il fatto che C

da una parte allaltra del prodotto scalare compare un termine ex-

non `e formalmente simmetrico. Per renderlo tale basta modicarne

pu`o essere determinata algebricamente in modo semplice:

cos` come denito dalla

anch`e valga una

si dice trasformata di Fourier di e gode delle seguenti propriet`a:

. Qui, come ho detto, continueremo con

() non commutino. Come in quel caso

(), cio`e spostando a destra gli

in generale `e possibile mostrare

() non commutano vengono a crearsi termini misti.

10 equivale a sostituire lhamiltoniana classica con lhamiltoniana

You might also like