Professional Documents
Culture Documents
HW#4 For Montgomery Design and Analysis of Experiments
Uploaded by
studycamOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
HW#4 For Montgomery Design and Analysis of Experiments
Uploaded by
studycamCopyright:
Available Formats
Individual Homework #4 Design of Experiment and Analysis 2.33. Manually BO1 BO2 6.08 5.73 6.22 5.8 7.
99 8.42 7.44 6.84 6.48 6.43 7.99 8.76 6.32 6.32 7.6 7.62 6.03 6.59 7.52 7.67 mean sd
diff 0.35 0.42 -0.43 0.6 0.05 -0.77 0 -0.02 -0.56 -0.15 -0.051 0.441
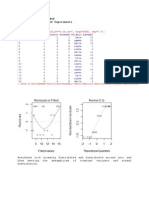
b) Ho = d=0 vs Ha: d0 to = d/Sd/sqrt(n) = -0.051/ 0.441/sqrt(10) = -0.3657 t0.025,9= 2.262 to < t0.025,9 No rejection of Null hypothesis. CI = to*Sd/10 d = -0.051 0.3159 The interval includes zero (0) so no rejection of null hypothesis. c) Ho = d=0 vs Ha: d>0 mean score of Date of birth 1 is greater than Date of birth 2 to = 0.3657< t0.05,9 =1.833 No rejection of Null hyp. Ho = d=0 vs Ha: d<0 mean score of Date of birth 1 is lower than Date of birth 2 to = -0.3657 < t0.05,9 =1.833 No rejection of Null hyp. R Solution a) Based on normal qq plot normal distribution of difference is reasonable.
Mean = -0.051 and s= 0.441
b) t.test(bo1, bo2, alternative ="two.sided", mu = 0, paired =TRUE, var.equal = FALSE, conf.level = 0.95) Paired t-test 95 percent confidence interval: -0.3664148 0.2644148 c). No evidence that birth order affect mean score (mean of differences) Ho: d=0 Ho: d>0 t.test(bo1, bo2, alternative ="greater", paired =TRUE) Paired t-test data: bo1 and bo2 t = -0.3658, df = 9, p-value = 0.6385 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: -0.3065927 Inf sample estimates: mean of the differences
-0.051 Ho: d=0 Ho: d<0 t.test(bo1, bo2, alternative ="less", paired =TRUE) Paired t-test data: bo1 and bo2 t = -0.3658, df = 9, p-value = 0.3615 alternative hypothesis: true difference in means is less than 0 95 percent confidence interval: -Inf 0.2045927 sample estimates: mean of the differences -0.051 2.34. a) Yes, they are different. p-value = 6.767e-05 km=c(1.186, 1.151, 1.322, 1.339, 1.200, 1.402, 1.365, 1.537, 1.559) lm=c(1.061, 0.992, 1.063, 1.062, 1.065, 1.178, 1.037, 1.086, 1.052) t.test(km, lm, alternative ="two.sided", mu = 0, paired =FALSE, var.equal = TRUE, conf.level = 0.95) Two Sample t-test data: km and lm t = 5.3302, df = 16, p-value = 6.767e-05 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 0.1649580 0.3828197 sample estimates: mean of x mean of y 1.340111 1.066222 b) p-value = 6.767e-05
c) t.test(km, lm, alternative ="two.sided", paired =TRUE) Paired t-test 95 percent confidence interval: 0.1700423 0.3777355 d) Data for Karlsruhe method appears to be normally distributed but data for Lehigh method is not normally distributed
e) Difference appears to be normally distributed based on normal qq plot
d) In the same way as the normality is a key assumption for one or two sample t test it is for a paired t test. In the case of paired t-test the samples are not drawn from independent populations. By taking the difference the bias (non independence) is relieved and the data is more normally distributed.
You might also like
- MINITAB TrainingDocument121 pagesMINITAB Trainingsriramc100% (6)
- Applied Linear Statistical Models 5th Edition Student S Solutions Manual PDFDocument111 pagesApplied Linear Statistical Models 5th Edition Student S Solutions Manual PDFGuilherme Marthe100% (1)
- Aczel Business Statistics Solutions Ch8-12Document112 pagesAczel Business Statistics Solutions Ch8-12Ruchi Patel100% (4)
- Solution Manual For Interactive Statistics Classic Version 3rd Edition Martha AliagaDocument15 pagesSolution Manual For Interactive Statistics Classic Version 3rd Edition Martha AliagaTiffanyMilleredpn100% (38)
- Ch02 SolutionDocument38 pagesCh02 SolutionSharif M Mizanur Rahman90% (10)
- On Measures of Entropy and InformationDocument18 pagesOn Measures of Entropy and Informationyounge994No ratings yet
- SUSS BSBA: BUS105 Jul 2020 TOA AnswersDocument10 pagesSUSS BSBA: BUS105 Jul 2020 TOA AnswersAzido Azide100% (1)
- Moving Average MethodDocument48 pagesMoving Average MethodShobhit Saxena100% (1)
- ExperimentosDocument680 pagesExperimentosGerardo Lopez100% (4)
- Final SBE-FINALSDocument11 pagesFinal SBE-FINALSVika BodokiaNo ratings yet
- Test 18Document2 pagesTest 18umamiNo ratings yet
- AsignmentDocument5 pagesAsignmenteliasNo ratings yet
- Stat FinalDocument8 pagesStat FinalJacob SchuitemanNo ratings yet
- Part III Review Solutions: X Is The Mean Score of TheDocument7 pagesPart III Review Solutions: X Is The Mean Score of TheLuciano AngrisaniNo ratings yet
- Individual Homework #3 Design of Experiment AnalysisDocument6 pagesIndividual Homework #3 Design of Experiment AnalysisstudycamNo ratings yet
- Measure of AssociationDocument5 pagesMeasure of AssociationAbha goyalNo ratings yet
- Graduate Statistics AssignmentsDocument7 pagesGraduate Statistics AssignmentsGraciously ElleNo ratings yet
- MHA 610 Week 4 AssignmentDocument7 pagesMHA 610 Week 4 Assignmentthis hihiNo ratings yet
- Sol Testing 2Document5 pagesSol Testing 2Carl DarcyNo ratings yet
- HW 4 A 1Document11 pagesHW 4 A 1draconnoxNo ratings yet
- QTBDocument7 pagesQTBUmarNo ratings yet
- Final Exam SBDocument12 pagesFinal Exam SBPhan Đức PhươngNo ratings yet
- Teknik SimulasiDocument5 pagesTeknik SimulasiBee BaiiNo ratings yet
- Review ExercisesDocument2 pagesReview Exercisesabu tonNo ratings yet
- UDTKDocument42 pagesUDTKkatieduong2002No ratings yet
- Lecture-5-Characterization of Collection of Particles-2Document21 pagesLecture-5-Characterization of Collection of Particles-2DikshithaNo ratings yet
- Exercise 06 AnsDocument2 pagesExercise 06 AnsPo ToNo ratings yet
- S Lab5 2507 W10Document4 pagesS Lab5 2507 W10mikeface100% (1)
- Acceptance Sampling - AttributesDocument10 pagesAcceptance Sampling - AttributessajinirajithNo ratings yet
- EES 404Document10 pagesEES 404beemuriithi24No ratings yet
- Solutions Manual For Business Statistics 3e by Norean D Sharpe 0133866912Document13 pagesSolutions Manual For Business Statistics 3e by Norean D Sharpe 0133866912TimothyHilldpgoa100% (75)
- Regression With Dummy Variables Econ420 1Document47 pagesRegression With Dummy Variables Econ420 1shaharhr1No ratings yet
- Comparing Diabetes Rates by Education LevelDocument27 pagesComparing Diabetes Rates by Education LevelPalize QaziNo ratings yet
- Solution - Sample Test: MULTIPLE CHOICE: Answer KeyDocument4 pagesSolution - Sample Test: MULTIPLE CHOICE: Answer KeyaaxdhpNo ratings yet
- Random Variables GuideDocument12 pagesRandom Variables Guidei am the greatest1No ratings yet
- Name: Log: E:/chrome Downloads/new Stata14/New Stata14/assigment - SMCL Log Type: SMCL Opened On: 18 Apr 2021, 19:22:54Document8 pagesName: Log: E:/chrome Downloads/new Stata14/New Stata14/assigment - SMCL Log Type: SMCL Opened On: 18 Apr 2021, 19:22:54Tayyiba IshaqNo ratings yet
- Tarea 1 DisenoDocument20 pagesTarea 1 DisenoTatiana YaraNo ratings yet
- Assignment # 6 Solution: MS MS y T y T N NDocument6 pagesAssignment # 6 Solution: MS MS y T y T N Nsulaiman_GNo ratings yet
- Assignment 5Document6 pagesAssignment 5sandeep BhanotNo ratings yet
- General Linear Model Do MinitabDocument48 pagesGeneral Linear Model Do MinitabJose MadymeNo ratings yet
- Sampling Distribution of Sample Proportion: Lecture 3: Statistical Inference by Dr. Javed IqbalDocument2 pagesSampling Distribution of Sample Proportion: Lecture 3: Statistical Inference by Dr. Javed IqbalHamna AghaNo ratings yet
- Desarrollo Solemne 3 - ..Ipynb - ColaboratoryDocument4 pagesDesarrollo Solemne 3 - ..Ipynb - ColaboratoryCarola Araya100% (1)
- Assigment 2Document2 pagesAssigment 2Tran Thanh Thao (K16 DN)No ratings yet
- Problem Paper Appendix MASTERDocument7 pagesProblem Paper Appendix MASTERgggtdyfhuuoNo ratings yet
- (MAA 4.11) NORMAL DISTRIBUTION - SolutionsDocument10 pages(MAA 4.11) NORMAL DISTRIBUTION - SolutionsAli HalawiNo ratings yet
- PracticeFinalExamQuestions 2 2020winter AnswerDocument4 pagesPracticeFinalExamQuestions 2 2020winter AnswerCHARLES DARWIN GAINNo ratings yet
- Applied Linear Statistical ModelDocument111 pagesApplied Linear Statistical ModelJordan BrianNo ratings yet
- Solutions Chapter6Document19 pagesSolutions Chapter6Zodwa MngometuluNo ratings yet
- Problem Set 1Document26 pagesProblem Set 1samir880100% (2)
- Business Statistics Topic 3 Tutorial Solutions (Q1-Q10)Document4 pagesBusiness Statistics Topic 3 Tutorial Solutions (Q1-Q10)Beryl ChanNo ratings yet
- Review: α β 2 HA Ho 2Document5 pagesReview: α β 2 HA Ho 2Nikhil NaniNo ratings yet
- Pas Tut 5Document10 pagesPas Tut 5Đặng Thị Phương Nga 2KT-20ACNNo ratings yet
- ERRORS IN MEASUREMENTDocument5 pagesERRORS IN MEASUREMENTOwen MuloNo ratings yet
- Mehran Riaz - 17232720-016 - QTBDocument13 pagesMehran Riaz - 17232720-016 - QTBMehran MalikNo ratings yet
- Bon FerroniDocument3 pagesBon FerroniFrancais FordNo ratings yet
- Matched Pair+Hypothesis+TestingDocument8 pagesMatched Pair+Hypothesis+TestingAmarnathMaitiNo ratings yet
- Differences in Statistics TestsDocument6 pagesDifferences in Statistics TestsAlex Marzonia MorronNo ratings yet
- STA302 Mid 2010FDocument9 pagesSTA302 Mid 2010FexamkillerNo ratings yet
- Chapter 14 SolutionsDocument11 pagesChapter 14 SolutionsDonna StampsNo ratings yet
- Solution 09Document29 pagesSolution 09aroobafatima24No ratings yet
- SOA Course 3 SolutionsDocument40 pagesSOA Course 3 SolutionsHông HoaNo ratings yet
- Uji Hipotesis Statistik BiologiDocument8 pagesUji Hipotesis Statistik BiologiSayla NadaNo ratings yet
- Dispersion and deviance residuals explainedDocument14 pagesDispersion and deviance residuals explainedK6 LyonNo ratings yet
- ERROR ANALYSIS OF EXPERIMENTS A Manual For Engineering StudentsDocument49 pagesERROR ANALYSIS OF EXPERIMENTS A Manual For Engineering StudentsWaseem Ali AkbarNo ratings yet
- Design and Analysis of Experiments Ind HW#15Document3 pagesDesign and Analysis of Experiments Ind HW#15studycam100% (1)
- Applied Linear Regression HomeworksDocument6 pagesApplied Linear Regression Homeworksstudycam100% (1)
- The Bimolecular Binding EventDocument48 pagesThe Bimolecular Binding Eventstudycam100% (1)
- Design of Experiments and Analysis HW#19Document3 pagesDesign of Experiments and Analysis HW#19studycamNo ratings yet
- Experimental Design and Analysis Montgomerry HW#22Document4 pagesExperimental Design and Analysis Montgomerry HW#22studycam100% (1)
- Aromatic InteractionsDocument32 pagesAromatic Interactionsstudycam100% (1)
- Design and Analysis of Experiments HomeworkDocument5 pagesDesign and Analysis of Experiments HomeworkstudycamNo ratings yet
- Ind HW#15Document3 pagesInd HW#15studycam100% (1)
- Homework Design Analysis Experiments Significant FactorsDocument7 pagesHomework Design Analysis Experiments Significant Factorsstudycam100% (1)
- Design of Experiments and Analysis HW#21Document4 pagesDesign of Experiments and Analysis HW#21studycam100% (1)
- Design and Analysis of Experiments HW#17Document4 pagesDesign and Analysis of Experiments HW#17studycamNo ratings yet
- Homework 12 Design and Analysis of ExperimentsDocument3 pagesHomework 12 Design and Analysis of ExperimentsstudycamNo ratings yet
- Design and Analysis of Experiments HomeworksDocument3 pagesDesign and Analysis of Experiments HomeworksstudycamNo ratings yet
- Design of Experiments and Analysis HomeworksDocument3 pagesDesign of Experiments and Analysis HomeworksstudycamNo ratings yet
- Spectroscopy 1012 2012Document54 pagesSpectroscopy 1012 2012studycamNo ratings yet
- Design and Analysis of ExperimentsDocument6 pagesDesign and Analysis of ExperimentsstudycamNo ratings yet
- Design and Analysis of Experiments HW#7Document7 pagesDesign and Analysis of Experiments HW#7studycamNo ratings yet
- Design and Analysis of Experiment HW#9Document4 pagesDesign and Analysis of Experiment HW#9studycamNo ratings yet
- Design and Analysis of Experiments HW#10Document3 pagesDesign and Analysis of Experiments HW#10studycamNo ratings yet
- Spectroscopy April 2012 Volume 27 Number 4Document62 pagesSpectroscopy April 2012 Volume 27 Number 4studycamNo ratings yet
- Physiological Barriers To Drug AbsorptionDocument41 pagesPhysiological Barriers To Drug AbsorptionstudycamNo ratings yet
- Design and Analysis of Experiments HW#8Document2 pagesDesign and Analysis of Experiments HW#8studycamNo ratings yet
- Design and Analysis of Experiment HomeWork # 5Document8 pagesDesign and Analysis of Experiment HomeWork # 5studycamNo ratings yet
- Individual Homework #3 Design of Experiment AnalysisDocument6 pagesIndividual Homework #3 Design of Experiment AnalysisstudycamNo ratings yet
- Individual Homework #3 Design of Experiment AnalysisDocument6 pagesIndividual Homework #3 Design of Experiment AnalysisstudycamNo ratings yet
- Physiological Barriers To Drug AbsorptionDocument41 pagesPhysiological Barriers To Drug AbsorptionstudycamNo ratings yet
- Non Linear Least Squares Curve Fitting With Microsoft Excel SolverDocument3 pagesNon Linear Least Squares Curve Fitting With Microsoft Excel SolverstudycamNo ratings yet
- Chi-Square Test ExplainedDocument13 pagesChi-Square Test ExplainedSunshine SamaresNo ratings yet
- MATH7340 Module 7 NotesDocument39 pagesMATH7340 Module 7 NotesdhsjhfdkjNo ratings yet
- BENG 2142 Statistics Chapter 1 SummaryDocument18 pagesBENG 2142 Statistics Chapter 1 SummaryMohammad FaisalNo ratings yet
- Hasil Analisis Data Dengan SPSS (Lanjutan) Lampiran 4 Hasil Uji KorelasiDocument12 pagesHasil Analisis Data Dengan SPSS (Lanjutan) Lampiran 4 Hasil Uji KorelasiThey AgueszNo ratings yet
- The Linear Regression ModelDocument25 pagesThe Linear Regression ModelPorshe56No ratings yet
- Chi-squared Test DefinitionDocument2 pagesChi-squared Test DefinitionSanta Dela Cruz NaluzNo ratings yet
- Factor Analysis: (Dataset1)Document5 pagesFactor Analysis: (Dataset1)trisnokompNo ratings yet
- Essentials of Econometrics 4th Edition Gujarati Solutions ManualDocument13 pagesEssentials of Econometrics 4th Edition Gujarati Solutions Manualtalliagepersonp5r7c100% (29)
- Edexcel GCE: Statistics S1Document24 pagesEdexcel GCE: Statistics S1yvg95No ratings yet
- A Practical Overview On Comparison Discrete and Continuous Probability DistributionsDocument4 pagesA Practical Overview On Comparison Discrete and Continuous Probability Distributionsvikalp123123No ratings yet
- Step 1: State The Null and Alternative HypothesisDocument3 pagesStep 1: State The Null and Alternative HypothesisChristine Joyce BascoNo ratings yet
- Grade 3 Data Mining TechniquesDocument28 pagesGrade 3 Data Mining TechniquesstudyjunkyNo ratings yet
- Level 2 Statistics Inference Exemplar NCEADocument3 pagesLevel 2 Statistics Inference Exemplar NCEACallaNo ratings yet
- FINAL (SG) - PR 2 11 - 12 - UNIT 7 - LESSON 2 - Testing The Difference of Two MeansDocument27 pagesFINAL (SG) - PR 2 11 - 12 - UNIT 7 - LESSON 2 - Testing The Difference of Two MeansCamille Darcy AguilarNo ratings yet
- Introduction to Statistical Hypothesis Testing in RDocument47 pagesIntroduction to Statistical Hypothesis Testing in RtrNo ratings yet
- IOER Descriptive and Inferential Gonzales NepthalieDocument39 pagesIOER Descriptive and Inferential Gonzales NepthalieMITZHE GAE MAMINONo ratings yet
- MLC Cheat SheetDocument12 pagesMLC Cheat Sheet18729No ratings yet
- PROBLEM SET 1 and 2 - 2 - 2 PDFDocument7 pagesPROBLEM SET 1 and 2 - 2 - 2 PDFMaharghya BiswasNo ratings yet
- Single Case Time Series With Bayesian Analysis A Practitioner S GuideDocument13 pagesSingle Case Time Series With Bayesian Analysis A Practitioner S GuideCai PengpengNo ratings yet
- Dilla University: College of Natural and Computational SciencesDocument38 pagesDilla University: College of Natural and Computational SciencesHabtamu Hailu100% (1)
- VezelDocument20 pagesVezelsarwar41ssNo ratings yet
- Gretl Guide (301 350)Document50 pagesGretl Guide (301 350)Taha NajidNo ratings yet
- Homework Solutions For Chapter 13Document17 pagesHomework Solutions For Chapter 13api-234237296No ratings yet
- Yates PDFDocument8 pagesYates PDFMilena MilovanovićNo ratings yet
- Unit 7 Chi Square TestDocument23 pagesUnit 7 Chi Square TestumapanneerselvamNo ratings yet
- Unit I Probability and Random Variables: S. No Questions BT Level Part - ADocument20 pagesUnit I Probability and Random Variables: S. No Questions BT Level Part - AShanmugam VaradhanNo ratings yet
- Reducing Aht - Business Credit Services: By: Subhash MandalDocument46 pagesReducing Aht - Business Credit Services: By: Subhash MandalFrinces MarvidaNo ratings yet