ENGI 5432 2. Surface Integrals Page 2.

01
2. Surface Integrals
This chapter introduces the theorems of Green, Gauss and Stokes. Two different
methods of integrating a function of two variables over a curved surface are developed.
The sections in this chapter are:
2.1 Line Integrals
2.2 Greens Theorem
2.3 Path Independence
2.4 Surface Integrals - Projection Method
2.5 Surface Integrals - Surface Method
2.6 Theorems of Gauss and Stokes; Potential Functions
ENGI 5432 2.1 Line Integrals Page 2.02
2.1 Line Integrals
Two applications of line integrals are treated here: the evaluation of work done on a
particle as it travels along a curve in the presence of a [vector field] force; and the
evaluation of the location of the centre of mass of a wire.
Work done:
The work done by a force F in moving an elementary distance r along a curve C is
approximately the product of the component of the force in the direction of r and the
distance | r | travelled:
cos W F F r r
v
v v
g
Integrating along the curve C yields the total work done by the force F in moving along
the curve C:
C
W

F dr
v
v
g
( )
1 2 3 1 2 3
1
0
t
t
C
dx dy dz
f dx f dy f dz f f f dt
dt dt dt
_
+ + + +

,

C
C
d
W dt
dt

r
F dr F
v
v v
v
g g
ENGI 5432 2.1 Line Integrals Page 2.03
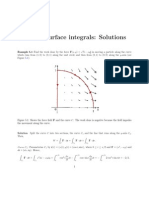
Example 2.1.1
Find the work done by
, , y x z F
v
in moving around the curve C (defined in
parametric form by x = cos t , y = sin t , z = 0 , 0 t 2 ).
, , sin , cos , 0
C
y x z t t F
v
cos , sin , 0 sin , cos , 0
d d
t t t t
dt dt

r
v
2 2
sin cos 0 1
d
t t
dt
+ +
r
F
v
v
g
2
2
0
0
1 2
d
W dt dt
dt

r
F
v
v
g
Note that
1
v
d
dt
F
d
dt

r
F
F v
r
v
v
g
v
g
v
everywhere on the curve C, so that
1 2 W C
(the length of the path around the circle).
Also note that

, , curl 2 y x z F F k
v v
everywhere in
3

.
The lesser curvature of the circular lines of force further away from the z axis is balanced
exactly by the increased transverse force, so that curl F is the same in all of
3

.
We shall see later (Stokes theorem, page 2.40) that the work done is also the normal
component of the curl integrated over the area enclosed by the closed curve C. In this
case
( ) ( )
( )
2

2 1 2 W A F n k k
v v
g g
.
ENGI 5432 2.1 Line Integrals Page 2.04
Example 2.1.1 (continued)
Example 2.1.2
Find the work done by
, , x y z F
v
in moving around the curve C (defined in
parametric form by x = cos t , y = sin t , z = 0 , 0 t 2 ).
, , cos , sin , 0
C
x y z t t F r
v
v
cos , sin , 0 sin , cos , 0
d d
t t t t
dt dt

r
v
cos sin sin cos 0 0
d
t t t t
dt
+ +
r
F
v
v
g
2
0
0 0 W dt

In this case, the force is orthogonal to the direction of motion at all times and no work is
done.
ENGI 5432 2.1 Line Integrals Page 2.05
If the initial and terminal points of a curve C are identical and the curve meets itself
nowhere else, then the curve is said to be a simple closed curve.
Notation:
When C is a simple closed curve, write
C

F dr
v
v
g
as
C

F dr
v
v
g
.
F is a conservative vector field if and only if
0
C

F dr
v
v
g
for all simple closed curves
C in the domain.
Be careful of where the endpoints are and of the order in which they appear (the
orientation of the curve). The identity
1 0
0 1
t t
t t
d d
dt dt
dt dt


r r
F F
v v
v v
g g
leads to the result
C C


F dr F dr
v v
v v
g g
i j simple closed curves C
Another Application of Line Integrals: The Mass of a Wire
Let C be a segment (t
0
t t
1
) of wire of line density (x, y, z). Then
( ) , , m x y z s
1
0
t
t
C
C
ds ds
m ds dt dt
dt dt

First moments about the coordinate planes:
m s M r r
v
v v

1
0
t
t
ds
dt
dt

M r
v
v
The location
r
v
of the centre of mass of the wire is , where
m

M
r
v
v
2 2 2
1 1
0 0
, and .
t t
t t
ds ds ds d dx dy dz
dt m dt
dt dt dt dt dt dt dt

_ _ _
+ +

, , ,

r
M r
v
v
v
ENGI 5432 2.1 Line Integrals Page 2.06
Example 2.1.3
Find the mass and centre of mass of a wire C (described in parametric form by
x = cos t , y = sin t , z = t , t ) of line density = z
2
.
Let c = cos t , s = sin t . [The shape of the wire is
one revolution of a helix,
, , , , 1
d
c s t s c
dt

r
r
v
v
aligned along the z axis,
centre the origin.]
( )
2
2 2
1 2
ds
s c
dt
+ +
2 2
z t
2
3
2 2
3
C
ds t
m ds dt t dt
dt

1

1
]

3
2
2
3
m
1
0
2 2 3
2 , ,
t
t
ds
dt t c t s t dt
dt

M r
v
v
x component:
Integration by parts.
( )
2 2
2 2 t c dt t s tc
1
+
]
( )
2 2
2 2 t c dt t s tc


1
+
]
( ) ( ) 0 2 0 2 4 +
ENGI 5432 2.1 Line Integrals Page 2.07
Example 2.1.3 (continued)
y component:
For all integrable functions f (t) and for all constants a note that
( )
( )
( ) ( )
0
0 if is an ODD function
2 if is an EVEN function
a
a
a
f t
f t dt
f t dt f t

'

2
sin t t is an odd function
2
0 t s dt

z component:
t
3
is also an odd function
3
0 t dt

Therefore

4 2 M i
v
2 3
3 6

4 2
2 2 m



M
r i i
v
v
The centre of mass is therefore at 2
6
, 0, 0

,
ENGI 5432 2.2 Greens Theorem Page 2.08
2.2 Greens Theorem
Some definitions:
A curve C on 1
2
(defined in parametric form by ( ) ( ) ( )

, t x t y t + r i j
v
a t b) is
closed iff (x(a), y(a)) = (x(b), y(b)) .
The curve is simple iff ( ) ( )
1 2
t t r r
v v
for all t
1
, t
2
such that a < t
1
< t
2
< b ;
(that is, the curve neither touches nor intersects itself, except possibly at the end points).

Example 2.2.1
Two simple curves:
open closed
Two non-simple curves:
open closed
ENGI 5432 2.2 Greens Theorem Page 2.09
Orientation of closed curves:
A closed curve C has a positive orientation iff a point r(t) moves around C in an
anticlockwise sense as the value of the parameter t increases.
Example 2.2.2
Positive orientation Negative orientation
Let D be the finite region of 1
2
bounded by C. When a particle moves along a curve
with positive orientation, D is always to the left of the particle.
For a simple closed curve C enclosing a finite region D of 1
2
and for any vector function
1 2
, f f F
v
that is differentiable everywhere on C and everywhere in D,
Greens theorem is valid:
2 1
C
D
f f
dA
x y
_



,

F dr
v
v
g
i
The region D is entirely in the xy-plane, so that the unit normal vector everywhere on D is
k. Let the differential vector dA = dA k , then Greens theorem can also be written as
( ) ( )

curl
C D D
dA

F dr F k F dA
v v v v v
v
g g g
i

( )
2 1
1 2 1 2
, ,
C
D
f f
f f dx dy f dx f dy dA
x y
_
+


,

F dr
v
v
g g
i
and
T
T
2 1
1 2
det det
f f
x y
x y
f f
1
1
1

1
1

]
1
]
F
v
v

z component of F
v v

Greens theorem is valid if there are no singularities in D.

ENGI 5432 2.2 Greens Theorem Page 2.10
Example 2.2.3

, 0 :
x
r
F
v
Greens theorem is valid for curve C
1
but not for curve C
2
.
There is a singularity at the origin, which curve C
2
encloses.
Example 2.2.4
For
, x y x y + F
v
and C as shown, evaluate
.
C

F dr
v
v
g
i
C PQ QR RP
+ +

F dr F dr F dr F dr
v v v v
v v v v
g g g g
i
ENGI 5432 2.2 Greens Theorem Page 2.11
Example 2.2.4 (continued)
, x y x y + F
v
Everywhere on the line segment from P to Q, y = 2 x (and the parameter t is just x)
, 2 1, 1 and 2, 2 2
d
x x x
dx

r
r F
v
v
v
( ) ( ) ( )
0
2
2
0 0
2 2
2 2 2 4 2 4
PQ
x dx x dx x x 1
]

F dr
v
v
g
= (0 0) (8 4) = 4
Everywhere on the line segment from Q to R, y = 2 + x
, 2 1, 1 and 2 2, 2
d
x x x
dx
+ +
r
r F
v
v
v
( ) ( )
2
2
0
2 2
0 0
2 2 2 2
QR
x dx x dx x


1 +
]

F dr
v
v
g
= 4 0 = 4
Everywhere on the line segment from R to P, y = 0
, 0 1, 0 and ,
d
x x x
dx

r
r F
v
v
v
( )
2
2
2
2 2
2 2
0
2
RP
x
x dx x dx

1
+
1
]

F dr
v
v
g
= 2 2 = 0
4 4 0 0
C
+ +

F dr
v
v
g
i
ENGI 5432 2.2 Greens Theorem Page 2.12
Example 2.2.4 (continued)
OR use Greens theorem!
( ) ( )
1 2
det 1 1 0 x y x y x y
x y
f f
1

1
+
1

1
]
everywhere on D
2 1
0 0
D D
f f
dA dA
x y
_



,

By Greens theorem it then follows that
0
C

F dr
v
v
g
i
ENGI 5432 2.2 Greens Theorem Page 2.13
Example 2.2.5
Find the work done by the force
2
, x y y F
v
in one circuit of the unit square.
By Greens theorem,
2 1
C
D
f f
W dA
x y
_



,

F dr
v
v
g
i
( ) ( )
2 2 1
0
f f
y x y x
x y x y



The region of integration is the square 0 < x < 1, 0 < y < 1
( )
1 1
0 0
D
W x dA x dy dx

[ ] ( )
1 1 1 1
1
0
0 0 0 0
1 1 0 x dy dx x y dx x dx
_


,

1
2
0
1 1
0
2 2 2
x 1
+
1
]
Therefore
1
2
W
The alternative method (using line integration instead of Greens theorem) would involve
four line integrals, each with different integrands!
ENGI 5432 2.3 Path Independence Page 2.14
2.3 Path Independence
Gradient Vector Fields:
If , F
v v
then
,
x y



F
v
2 1
0
yx xy
f f
x y




(provided that the second partial derivatives are all continuous).
It therefore follows, for any closed curve C and twice differentiable potential function
that
0
C

dr
v
v
g

Path Independence
If ( )
or F F
v v v v

, then is a potential function for F.
Let the path C travel from point P
o
to point P
1
:
C C C C
dx dy dz d
x y z


_
+ +


,

F dr dr
v v
v v
g g
[chain rule]
[ ] ( ) ( )
1
0
1 0
P
P
P P
which is independent of the path C between the two points.
Therefore
work done difference in
by between endpoints of C

_ _

, ,
v

( ) ( ) 0
C
P P

dr
v
v
g

[work done = potential difference]

ENGI 5432 2.3 Path Independence Page 2.15
Domain
A region of
2

is a domain if and only if

1) For all points P
o
in , there exists a circle, centre P
o
, all of whose interior points
are inside ; and
2) For all points P
o
and P
1
in , there exists a piecewise smooth curve C, entirely in
, from P
o
to P
1
.
Example 2.3.1 Are these domains?
{ (x, y) | y > 0 } { (x, y) | x 0 }
YES (but not simply connected) NO
If a domain is not specified, then, by default, it is assumed to be all of 1
2
.
ENGI 5432 2.3 Path Independence Page 2.16
When a vector field F is defined on a simply connected domain , these statements are
all equivalent (that is, all of them are true or all of them are false):
F
v v
for some scalar field that is differentiable everywhere in ;
F is conservative;

F dr
v
v
g
is path-independent (has the same value no matter which path within
is chosen between the two endpoints, for any two endpoints in );

start end
C

F dr
v
v
g
(for any two endpoints in );

0
C

F dr
v
v
g
for all closed curves C lying entirely in ;

2 1
f f
x y

everywhere in ; and
F 0
v v v
everywhere in (so that the vector field F is irrotational).
There must be no singularities anywhere in the domain in order for the above set of
equivalencies to be valid.
Example 2.3.2
Evaluate
( ) ( ) ( )
2
2 3
C
x y dx x y dy + + +
where C is any piecewise-smooth curve from
(0, 0) to (1, 2).
2
2 , 3 x y x y + + F
v
is continuous everywhere in
2

2 1
1
f f
x y



F
v
is conservative and F
v v

2
2 and 3 x y x y
x y

+ +

A potential function that has the correct first partial derivatives is
2 3
x xy y + +
( )
( )
( ) ( )
1,2
0,0
1 2 8 0 0 0
C

1
+ + + +
1
]

F dr
v
v
g
Therefore
( ) ( ) ( )
2
2 3 11
C
x y dx x y dy + + +

ENGI 5432 2.3 Path Independence Page 2.17

Example 2.3.3 (A Counterexample)
Evaluate
C

F dr
v
v
g
i , where
2 2 2 2
,
y x
x y x y

+ +
F
v
and C is the unit circle, centre at the
origin.
F
v
is continuous everywhere except (0, 0)

is not simply connected. [ is all of
2

except (0, 0).]

( )
2 1
2 2
2
2 2
f f x y
x y
x y



+
everywhere in
We cannot use Greens theorem, because
F
v
is not continuous everywhere inside C
(there is a singularity at the origin).
Let c = cos t and s = sin t then
( ) , 0 2 , c s t s c < r r
v v
2 2 2 2
, ,
s c
s c
c s c s

+ +
F
v
( )
2 2
2
2 2
0
0 0
1
C
s c dt dt t


1

]
F dr
v
v
g
i
Therefore
2
C

F dr
v
v
g
i
Note:
0
C

F dr
v
v
g
i , but
everywhere on
, , where Arctan
x
k
y

_
+

,
F
v v

The problem is that the arbitrary constant k is ill-defined.

ENGI 5432 2.3 Path Independence Page 2.18
Example 2.3.3 (continued)
Let us explore the case when k = 0.
Contour map of
Arctan 0
x
y

_
+

,
We encounter a conflict in the value of the potential function .
Solution: Change the domain to the simply connected domain
2
except the
non-negative axis x
_


,

then the potential function

can be well-defined, but no curve in can enclose the

origin.