Matematicaspara Ing IIISantiago Relos 24 de Mayo 2013

Matemticas para Ingeniera III
Variable Compleja, Anlisis de, Fourier, Anlisis Vectorial

MSc. Santiago Relos P.
Universidad Privada Boliviana
24 de mayo de 2013
2
ndice General
1 Nmeros complejos 7
1.1 El conjunto C de los nmeros complejos . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1.1 Propiedades . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
1.1.2 La extensin de R a C y notacin usual de un nmero complejo . . . . . . . . 8
1.1.3 La conjugada de un nmero complejo . . . . . . . . . . . . . . . . . . . . . . 9
1.2 Representacin grca de un nmero complejo
1
. . . . . . . . . . . . . . . . . . . . . 11
1.2.1 Representacin grca de la suma y resta . . . . . . . . . . . . . . . . . . . . 12
1.2.2 Representacin grca de la conjugada . . . . . . . . . . . . . . . . . . . . . . 12
1.3 El mdulo de un nmero complejo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.4 Forma polar y el argumento de un nmero complejo . . . . . . . . . . . . . . . . . . 15
1.4.1 Forma polar . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4.2 Argumento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.4.3 Forma exponencial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.4.4 Races de un nmero complejo . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.5 Conjuntos abiertos y cerrados . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2 Funciones complejas de variable compleja 25
2.1 Funciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.2 Transformaciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.3 Lmites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.3.1 La denicin de lmite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.3.2 El lmite de funciones complejas como el lmite de funciones reales . . . . . . 30
2.3.3 Teoremas sobre lmites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.3.4 Lmites en el innito . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.4 Continuidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.5 Derivadas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
1
Nota histrica. (Extraida de Historia de la matemtica de Carl B. Boyer, Alianza editorial 1968) La represen-
tacin grca de los nmeros complejos haba sido descubierta ya en 1797 por Caspar Wessel (1745-1818) y publicada
en la revista de la academia de ciencias danesa en 1798, pero lo cierto es que la obra de Wessel pas desapercibida
prcticamente, as el plano de los nmeros complejos suele llamarse plano de Gauss, a pesar de que Gauss no public
sus ideas al respecto hasta unos 30 aos mas tarde. Desde la poca de Girard era bien conocido que los nmeros reales
positivos, cero y negativos se pueden representar en correspondencia con los puntos de una recta. Wallis haba llegado
incluso a sugerir que los nmeros imaginarios puros se podran representar por los puntos de una recta perpendicular
al eje de los nmeros reales. Y, sin embargo, sorprendentemente nadie antes de Wessel y Gauss pens en franquear la
obvia etapa de considerar las partes real e imaginaria pura de un nmero complejo a + ib como las dos coordenadas
rectangulares de un punto en el plano, al cual estaria asociado dicho nmero complejo y viceversa. Ver es creer, bien
cierto es, y las viejas ideas acerca de la no existencia de los nmeros imaginarios fueron abandonadas por casi todos
los matemticos.
3
4 NDICE GENERAL
2.5.1 La denicin de derivada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
2.5.2 Teoremas sobre la derivada . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.5.3 Las ecuaciones de Cauchy-Rieman . . . . . . . . . . . . . . . . . . . . . . . . 33
2.6 Funciones analticas, enteras y armnicas . . . . . . . . . . . . . . . . . . . . . . . . 35
2.6.1 Funciones analticas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.6.2 Funciones enteras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.6.3 Funciones armnicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.7 Funciones elementales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.7.1 Funcin exponencial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.7.2 Funciones trigonomtricas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.7.3 Funciones hiperblicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
3 Anlisis de Fourier 43
3.1 Aspectos bsicos de la serie de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.1.1 Introduccin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.2 La serie de Fourier de una funcin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
3.2.1 Clculo de las constantes a
n
, b
n
. . . . . . . . . . . . . . . . . . . . . . . . . . 47
3.3 Series de fourier en senos y cosenos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
3.3.1 El caso de una funcin par . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.3.2 El caso de una funcin impar . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
3.3.3 Desarrollo de una funcin en senos y cosenos . . . . . . . . . . . . . . . . . . 57
3.4 Convergencia de la serie de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
3.4.1 Convergencia en los extremos . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
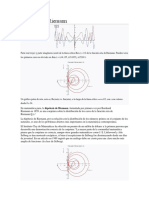
3.4.2 El fenmeno de Gibbs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
3.5 Derivacin e integracin de las series de Fourier . . . . . . . . . . . . . . . . . . . . . 61
3.5.1 Integracin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
3.5.2 Derivacin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
3.6 La serie de Fourier compleja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
3.7 Una aplicacin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.7.1 La ecuacin del calor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.7.2 La ecuacin de la onda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
4 La transformada de Fourier 69
4.1 La integral de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
4.2 La integral de Fourier compleja y la transformada de Fourier . . . . . . . . . . . . . 72
4.3 Propiedades de la transformada de Fourier . . . . . . . . . . . . . . . . . . . . . . . . 75
4.4 Convolucin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
5 Operaciones diferenciales 85
5.1 El operador Nabla . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
5.2 Funciones escalares y funciones vectoriales . . . . . . . . . . . . . . . . . . . . . . . . 85
5.3 Gradiente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
5.4 Divergencia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
5.5 Rotacional . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
NDICE GENERAL 5
6 La integral de supercie 91
6.1 La denicin de integral de supercie . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
6.2 Clculo de la integral de supercie . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
6.3 Teorema de la divergencia de Gauss . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
7 Coordenadas curvilneas 99
7.1 La denicin de coordenadas curvilneas . . . . . . . . . . . . . . . . . . . . . . . . . 99
7.2 Supercies y lneas de coordenadas . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
7.3 Vectores bsicos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
7.4 Gradiente divergencia y rotacional . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
6 NDICE GENERAL
Captulo 1
Nmeros complejos
En este captulo se inicia el estudio del campo de nmeros complejos, se dene un nmero complejo,
se estudian sus propiedades y resuelven problemas con nmeros complejos.
Entre otras, se tienen las siguientes aplicaciones en ingeniera.
Ingeniera electrnica, en la descripcin de seales peridicas: Anlisis de Fourier, re-
sistencias, capacidades e inductores.
Fsica: Mecnica Cuntica, relatividad especial y la relatividad general.
Matemticas: Ecuaciones diferenciales, Fractales, geometra.
Telecomunicaciones
1.1 El conjunto C de los nmeros complejos
El conjunto de nmeros complejos C es el conjunto de pares de nmeros reales z = (x, y) donde x,
y son nmeros reales. La igualdad de puntos en C se dene como (x, y) = (a, b) si x = a y y = b.
Las operaciones de suma y producto estn denidos por:
Suma:
(x
1
, y
1
) + (x
2
, y
2
) = (x
1
+x
2
, y
1
+y
2
)
Producto:
(x
1
, y
1
) (x
2
, y
2
) = (x
1
x
2
y
1
y
2
, x
1
y
2
+x
2
y
1
)
1.1.1 Propiedades
Sobre la conmutatividad
Para todo z
1
, z
2
C se cumple:
z
1
+z
2
= z
2
+z
1
y z
1
z
2
= z
2
z
1
.
7
8 CAPTULO 1. NMEROS COMPLEJOS
Sobre el cero y el uno
El cero en este conjunto es (0, 0) , ntese que para todo nmero complejo z = (x, y) se tiene:
(0, 0) +z = z.
Por otra parte el uno de este conjunto es (1, 0) , ntese que para todo nmero complejo z = (x, y) se
tiene:
(1, 0) z = z
Sobre el inverso aditivo y el inverso multiplicativo
Sea z = (x, y) y w = (a, b) tal que z + w = (0, 0) , es fcil probar que w = (x, y) . El nmero
complejo w se llama inverso aditivo de z.
Sea z = (x, y) = (0, 0) , y w = (a, b) tal que zw = (1, 0) , entonces empleando la denicin de
producto e igualdad de nmeros complejos:
zw = (xa yb, xb +ya) = (1, 0)
por tanto
xa yb = 1
xb +ya = 0
resolviendo el sistema se encuentra:
a =
x
x
2
+y
2
b =
y
x
2
+y
2
as w =
_
x
x
2
+y
2
,
y
x
2
+y
2
_
. El nmero w se llama inverso multiplicativo de z, usualmente se
denotar con z
1
, es decir,
(x, y)
1
=
_
x
x
2
+y
2
,
y
x
2
+y
2
_
La unidad imaginaria
El nmero complejo i = (0, 1) tiene la propiedad,
i
2
= (0, 1) (0, 1) = (0 1, 0 + 0) = (1, 0)
el nmero complejo i se llamar unidad imaginaria.
1.1.2 La extensin de R a C y notacin usual de un nmero complejo
La aplicacin x (x, 0) de R en C identica el nmero real x con el nmero complejo (x, 0) . Via
esta identicacin, es posible extender R a C. Esto tiene las siguientes consecuencias:
1.1. EL CONJUNTO C DE LOS NMEROS COMPLEJOS 9
Consecuencias
1. El cuadrado de la unidad imaginaria es:
i
2
= (1, 0) = 1
ntese que podramos interpretar a i como i =
1.
2. El nmero complejo z = (x, y) se escribe como:
z = (x, y)
= (x, 0) + (0, y)
= (1, 0) x + (0, 1) y
= x +iy,
sta es la forma usual de escribir un nmero complejo.
En z = x + iy, x se llama parte real y el nmero y se llama parte imaginaria. Se denotan
respectivamente con:
x = Re z, y = Imz
por tanto: z = Re z +i Imz.
Las operaciones suma y producto
Con la nueva forma de escribir un nmero complejo, se vuelve a denir la suma y producto de
nmeros complejos. Sean z
1
= x
1
+iy
1
y z
2
= x
2
+iy
2
, entonces:
z
1
+z
2
= (x
1
+iy
1
) + (x
2
+iy
2
)
= (x
1
+x
2
) +i (y
1
+y
2
) ,
es decir la suma se realiza siguiente la regla: parte real con parte real y parte imaginaria con parte
imaginaria. Por otra parte:
z
1
z
2
= (x
1
+iy
1
) (x
2
+iy
2
)
= x
1
x
2
+x
1
(iy
2
) + (iy
1
) x
2
+ (iy
1
) (iy
2
)
= (x
1
x
2
y
1
y
2
) +i (x
1
y
2
+x
2
y
1
)
ntese que se a hecho la multiplicacin como en cualquier par de binomios, slo se toma en cuenta
que i
2
= 1.
1.1.3 La conjugada de un nmero complejo
Sea z = a +ib, la conjugada de este nmero complejo se dene por
z = a ib,
es decir, se cambia de signo a la parte imaginaria.
Propiedades
Para z
1
y z
2
nmeros complejos se cumplen:
1. z
1
+z
2
= z
1
+z
2
2. z
1
z
2
= z
1
z
2
3. (z
1
) (z
2
) = (z
1
) (z
2
)
4.
_
z
1
z
2
_
=
z
1
z
2
5. Si z = a +ib, entonces
zz = (a +ib) (a ib)
= a
2
iab +iba i
2
b
2
= a +b
2
6. Si z = a +ib, entonces
1
z
=
z
zz
=
a ib
a
2
+b
2
resultado que coincide con el clculado en la seccin 1.1.1 pgina 8.
7. Si z es un nmero real claramente z = z.
8. Si la parte real de un nmero complejo es cero, el nmero complejo se llama imaginario puro.
Si z es imaginario puro, entonces z = z.
Ejercicios propuestos
1. Probar que para z
1
y z
2
nmeros complejos se cumplen:
(a) z
1
+z
2
= z
1
+z
2
(b) z
1
z
2
= z
1
z
2
(c) (z
1
) (z
2
) = (z
1
) (z
2
)
(d)
_
z
1
z
2
_
=
z
1
z
2
2. Pruebe que:
(a) (1 +i) +
(2 + 3i)
4
2 + 2i
=
235
4
+
3
4
i
(b) (a + 2i)
3
= a
3
12a +i
_
6a
2
8
_
(c)
1 +ix
3 + 4i

2 + 3i
1 +i
=
_
2
25
+
3
50
i
_
(2x 23 + 9i)
1.2. REPRESENTACIN GRFICA DE UN NMERO COMPLEJO
2
11
(d)
(1 + 2i) (1 3i)
3
(1 +i)
2
= 17 + 31i
(e)
_
2 + 4i
i
+
1 + 3i
1 +i
_
= 2 +i
3. Exprese lo siguiente en la forma x +iy, con x, y R
(a)
1 +k
2
ik
k i
1 +k
2
. Sol. i
(b)
_
44i
2+2i
_
555
2
+
_
4+4i
22i
_
555
2
. Sol. 0
(c) (1 +i)
6
. Sol. 8i
(d)
_
ai
25
i
32
_
3 + 4i
. Sol.
_
3
25
+
4
25
a
_
+
_
3
25
a +
4
25
_
i
(e)
(
2i)
2
(1i)
4
(
2+i)
4
. Sol.
92
81

40
81
i
2
(f) (x +iy) (u iv) (x iy) (u +iv). Sol. x
2
u
2
+x
2
v
2
+y
2
u
2
+y
2
v
2
4. Si x, y R, resolver: x
2
y
2
+ixy = 1 +ix. Sol. x =
2, y = 1.
1.2 Representacin grca de un nmero complejo
1
El nmero complejo z = a +ib se representa en el llamado Plano de Gauss que en realidad es una
copia de R
2
. El nmero complejo z = a +ib se representa como radio vector (a, b) como se muestra
1
Nota histrica. (Extraida de Historia de la matemtica de Carl B. Boyer, Alianza editorial 1968) La represen-
tacin grca de los nmeros complejos haba sido descubierta ya en 1797 por Caspar Wessel (1745-1818) y publicada
en la revista de la academia de ciencias danesa en 1798, pero lo cierto es que la obra de Wessel pas desapercibida
prcticamente, as el plano de los nmeros complejos suele llamarse plano de Gauss, a pesar de que Gauss no public
sus ideas al respecto hasta unos 30 aos mas tarde. Desde la poca de Girard era bien conocido que los nmeros reales
positivos, cero y negativos se pueden representar en correspondencia con los puntos de una recta. Wallis haba llegado
incluso a sugerir que los nmeros imaginarios puros se podran representar por los puntos de una recta perpendicular
al eje de los nmeros reales. Y, sin embargo, sorprendentemente nadie antes de Wessel y Gauss pens en franquear la
obvia etapa de considerar las partes real e imaginaria pura de un nmero complejo a + ib como las dos coordenadas
rectangulares de un punto en el plano, al cual estaria asociado dicho nmero complejo y viceversa. Ver es creer, bien
cierto es, y las viejas ideas acerca de la no existencia de los nmeros imaginarios fueron abandonadas por casi todos
los matemticos.
en el grco 1:
x
y
b i a z + =
a
b
1.2.1 Representacin grca de la suma y resta
x
y
x
y
1
z
2
z
2 1
z z +
1
z
2
z
2
z
2 1
z z
1.2.2 Representacin grca de la conjugada
x
y
b i a z + =
b
b
a
b i a z =
1.3. EL MDULO DE UN NMERO COMPLEJO 13
1. Sea z = a +ib. Representar grcamente z y zi.
2. Sea z = a +ib. Representar grcamente z y zi
1
.
3. Sea z = a +ib en el primer cuadrante, en que cuadrante se encuentra
a +ib
1 +i
?.
1.3 El mdulo de un nmero complejo
Sea z = a +ib un nmero complejo, el mdulo de este nmero complejo se dene por:
|z| =
_
a
2
+b
2
,
ntese que es la distancia del punto (a, b) al punto (0, 0).
Propiedades. El mdulo tiene las siguientes propiedades:
1. |z
1
z
2
| = |z
1
| |z
2
|
2.
z
1
z
2
=
|z
1
|
|z
2
|
, z
2
no nulo.
3. |z|
2
= zz
4. |z
1
+z
2
| |z
1
| +|z
2
| {desigualdad triangular}
5. El lugar geomtrico de puntos que satisfacen |z z
0
| = r, es la circunferencia centrada en el
origen y radio r.
1. Probar:
(a) Re (z) =
1
2
(z +z) ,
(b) Im(z) =
1
2i
(z z)
(c) Im(z) |Im(z)| |z|
2. Probar que para todos los nmeros complejos z, w se cumple:
(a) |z| |z w| +|w|
(b) ||z| |w|| |z w|
3. Determinar y gracar el lugar geomtrico de los puntos (x, y) tales que:
(a) z +z = 3. Sol. recta x = 3/2.
(b) z
2
+z
2
= 8. Sol. hiprbola x
2
y
2
= 4.
(c) z
2
z
2
= 4i. Sol. Hiprbola xy = 1.
(d) |z 2i| +|z i| = 8. Sol. Elipse
x
2
63/4
+
(y 3/2)
2
16
= 1.
(e) |z + 4| +|z 2| = 2. Sol. Ningn lugar geomtrico. (explique la razn)
(f) |z + 4| +|z 2| = 10. Sol. Elipse
(x + 1)
2
5
2
+
y
2
4
2
= 1.
4. Sea |z| = 2. Pruebe que

z 4w
1 zw
= 2,
donde w es otro nmero complejo tal que zw = 1.
5. Pruebe que para todo |z| = 2 se cumple:
1
4

z
2
+ 1
z
2
+ 8
5
4
Sug. Aplique |z
1
+z
2
| |z
1
| +|z
2
| y que |z
1
z
2
| |z
1
| |z
2
|
6. Pruebe que para todo nmero complejo z se cumple:
|z + 1|
1
2
o

z
2
+ 1
1.
Sug. Si la armacin no fuera cierta, se llega a una contradiccin aplicando propiedades de
mdulo.
7. Pruebe que
3 |z + 1| +
z
2
z + 1
13
4
para todos los nmeros complejos z tales que |z| = 1. Sug. Aplique |w|
2
= ww, a los mdulos,
as construir una funcin a una sola variable en el dominio [1, 1] .
8. Encontrar todos los nmeros z = 0 tales que z +
1
z
R. Sol. o z R o z tal que |z| = 1.
9. Pruebe que
_
19 + 7i
9 i
_
n
+
_
20 + 5i
7 + 6i
_
n
R. Sug. Nte que w R si y solo si w = w.
10. Sea z = 0. Si
z
3
+
1
z
3
2 entonces
z +
1
z
2. Sug. Desarrolle
_
z +
1
z
_
3
.
11. Resolver
|z| = 1
|z +z| = 4
Sol. no existe
1.4. FORMA POLAR Y EL ARGUMENTO DE UN NMERO COMPLEJO 15
12. Resolver
|z| = 1
z
2
+z
2
= 1
Sol.
3
2

1
2
i,
13. Resolver:
2z
2
+|z|
2
= 1
Sol. z = i
1.4 Forma polar y el argumento de un nmero complejo
1.4.1 Forma polar
Sean r, las coordenadas polares de (x, y) que corresponde al nmero complejo z = x+iy, entonces
x = r cos
y = r sin,
entonces:
z = r (cos +i sin) ,
se llama la forma polar del nmero complejo z. Claramente r =
_
x
2
+y
2
y es el ngulo
que se forma con el radio vector z y el eje positivo x, es claro que = arctan
_
y
x
_
. Debido a la
periodicidad de las funciones seno y coseno se tiene:
z = r (cos ( + 2n) +i sin( + 2n)) , n = 0, 1, 2, . . .
x
y

x
y
x
y
x
y
1.4.2 Argumento
Denicin 1.1 (argumento) El nmero de la forma polar de un nmero complejo, se llama
argumento del nmero complejo z y se denota por arg z = , es positiva si para su clculo se toma el
sentido contrario de las agujas del reloj y negativa en caso contrario, ms an, +2n sigue siendo
el argumento de z para todo entero n. El valor principal del argumento, denotado por Arg z es el
nico valor de arg z tal que < arg z .
Ejemplo 1.1 Algunos argumentos de z = 1 +i son:
/4, 7/4,
9
4
, etc.
x
y
4 /
4 / 7
estos se obtienen a partir de dar valores enteros a n en:
4
+ 2n o
7
4
+ 2n.
En este caso Arg (1 +i) =

4
, as la forma polar es:
1 +i =
2
_
cos

4
+i sin

4
_
Ejemplo 1.2 Considrese el nmero z = 34i, el argumento principal es Arg (3 4i) = arctan(4/3) ,
por tanto la forma polar es:
3 4i =
_
3
2
+ 4
2
_
cos
_
arctan
4
3
_
+i sin
_
arctan
4
3
__
= 5
_
cos
_
arctan
4
3
_
+i sin
_
arctan
4
3
__
x
y
1 2 3
1
2
3
4
) 3 / 4 arctan(
Teorema 1.2 (Propiedad del argumento) Sean z
1
, z
2
nmeros complejos, entonces dados dos
de los argumentos arg z
1
, arg z
2
o arg (z
1
z
2
) existe un valor del tercer argumento tal que arg (z
1
z
2
) =
arg z
1
+ arg z
2
.
Observacin. No se est diciendo que lo anterior sea cierto para cualquier argumento.
Ejemplo 1.3 Si z
1
= 1, z
2
= 2i, entonces z
1
z
2
= 2i, si se toma
arg (z
1
) = 3
arg (z
2
) =

2
arg (z
1
z
2
) =
3
2
claramente se tiene:
arg (z
1
z
2
) = arg (z
1
) + arg (z
2
)
1.4.3 Forma exponencial
Denimos la frmula de Euler como:
e
i
= cos +i sin
para todo nmero real . Con esta notacin un nmero complejo z se escribe como:
z = r (cos +i sin) = re
i
donde r = |z| y = arg z.
Propiedades
1. e
i
1
e
i
2
= e
i(
1
+
2
)
2. Si z = re
i
, entonces z
1
=
1
r
e
i
.
3. Si z
1
= r
1
e
i
1
, z
2
= r
2
e
i
2
, entonces
z
1
z
2
= r
1
r
2
e
i(
1
+
2
)
y
z
1
z
2
=
r
1
r
2
e
i(
1
2
)
4. Si z = re
i
, entonces z = re
i(+2n)
, para n = 0, 1, 2, . . . .
5. Dos nmeros complejos z
1
= r
1
e
i
1
y z
2
= r
2
e
i
2
son iguales si y solamente si
r
1
= r
2
y
1
=
2
+ 2k
donde k es algn entero.
6. La representacin geomtrica de
z = re
i
, (0 2)
es una representacin paramtrica de la circunferencia |z| = r centrada en el origen y radio r.
Ms an la circunferencia centrada en z
0
y radio r es
z = z
0
+re
i
, (0 2) .
x
y
r
O
x
y
O
0
z
z
i
re

i
re z =
i
re z z + =
0
1.4.4 Races de un nmero complejo
Como se sabe, empleando la forma exponencial de un nmero complejo z = x +iy se tiene:
z = re
i
, n = 0, 1, 2, . . .
donde r = |z| y = arctan
_
y
x
_
. Entonces:
z
n
= r
n
e
in
, n = 0, 1, 2, . . . ,
en el caso particular r = 1, mediante la aplicacin de la frmula de Euler se tiene el:
Teorema 1.3 (El teorema de Moivre) Para todo y todo entero n se verica:
(cos +i sin)
n
= cos (n) +i sin(n) .
El teorema de Moivre se emplea para calcular las races de un nmero complejo.
Sea n un entero y
w = z
1/n
,
entonces claramente z = w
n
. Empleando la forma polar escribamos:
z = re
i
w = Re
i
empleando el teorema de Moivre: w
n
= R
n
e
in
. Puesto que z = w
n
, se debe tener:
R
n
= r, n = + 2k, k = 0, 1, 2, . . .
de donde:
R = r
1/n
, =
+ 2k
n
, k = 0, 1, 2, . . .
luego:
w = r
1/n
e
i
_
+ 2k
n
_
= r
1/n
_
cos
+ 2k
n
+i sin
+ 2k
n
_
, k = 0, 1, 2, . . .
as hemos probado el siguiente teorema.
Teorema 1.4 Si n es un entero positivo, la raz n esima de z = re
i
est dado por
z
1/n
= r
1/n
_
cos
+ 2k
n
+i sin
+ 2k
n
_
,
para k = 0, 1, 2, . . . .
Observacin. Solamente son distintas n races, ms concretamente
si k = 0 : z
0
= r
1/n
_
cos

n
+i sin

n
_
si k = 1 : z
1
= r
1/n
_
cos
+ 2
n
+i sin
+ 2
n
_
.
.
.
si k = n 1 : z
n1
= r
1/n
_
cos
+ 2 (n 1)
n
+i sin
+ 2 (n 1)
n
_
para k = n, se tiene
z
n
= r
1/n
_
cos
+ 2n
n
+i sin
+ 2n
n
_
= r
1/n
(cos ( + 2) +i sin( + 2))
= r
1/n
(cos () +i sin())
= z
0
.
z
n+1
= z
1
, y as sucesivamente.
Observacin. Puesto que
_
cos
+ 2k
n
+i sin
+ 2k
n
_
= 1, cada raz tiene el mismo mdulo

r
1/n
, esto quiere decir que las races se encuentran en una circunferencia centrada en el origen y radio
r
1/n
.
Ejemplo 1.4 Determinaremos las races cuartas de z = 1 i.
En la forma polar z = 2
1/2
_
cos
_
4
_
+i sin
_
4
__
, por tanto las races cuartas estn dadas
por:
z
1/4
= 2
1/8
_
_
cos
_
_
4
+ 2k
4
_
_
+i sin
_
_
4
+ 2k
4
_
_
_
_
, k = 0, 1, 2, 3.
z
0
= 2
1/8
_
_
cos
_
_
4
+ 2 (0)
4
_
_
+i sin
_
_
4
+ 2 (0)
4
_
_
_
_
1. 0696 0. 2128i
z
1
= 2
1/8
_
_
cos
_
_
4
+ 2 (1)
4
_
_
+i sin
_
_
4
+ 2 (1)
4
_
_
_
_
0. 2128 + 1. 0696i
z
2
= 2
1/8
_
_
cos
_
_
4
+ 2 (2)
4
_
_
+i sin
_
_
4
+ 2 (2)
4
_
_
_
_
1. 0696 + 0. 2128i
z
3
= 2
1/8
_
_
cos
_
_
4
+ 2 (3)
4
_
_
+i sin
_
_
4
+ 2 (3)
4
_
_
_
_
0. 2128 1. 0696i
Las races se muestran en la siguiente gura. Ntese que las races forman los vrtices de un cuadrado.
-1.5 -1 -0.5 0 0.5 1 1.5
-1.5
-1
-0.5
0
0.5
1
1.5
0
z
1
z
3
z
2
z
x
y
Ejemplo 1.5 Determinaremos las races quintas de z = 8 + 6i
Un argumento se calcula de tan =
6
8
en el segundo cuadrante, luego = arctan
_
6
8
_
=
2. 4981; por otra parte el mdulo es r = |8 6i| = 10, luego:
z = 10
_
cos
_
arctan
_
6
8
__
+i sin
_
arctan
_
6
8
___
Ahora calculamos las races quintas:
z
1/5
= 10
1/5
_
_
_
_
cos
_
_
_
_
arctan
_
6
8
_
+ 2k
5
_
_
_
_
+i sin
_
_
_
_
arctan
_
6
8
_
+ 2k
5
_
_
_
_
_
_
_
_
, k = 0, 1, 2, 3, 4
z
0
= 10
1/5
_
_
_
_
cos
_
_
_
_
arctan
_
6
8
_
5
_
_
_
_
+i sin
_
_
_
_
arctan
_
6
8
_
5
_
_
_
_
_
_
_
_
1. 3912 + 0. 7593i
z
1
= 10
1/5
_
_
_
_
cos
_
_
_
_
arctan
_
6
8
_
+ 2
5
_
_
_
_
+i sin
_
_
_
_
arctan
_
6
8
_
+ 2
5
_
_
_
_
_
_
_
_
0. 29225 + 1. 5577i
z
2
= 10
1/5
_
_
_
_
cos
_
_
_
_
arctan
_
6
8
_
+ 4
5
_
_
_
_
+i sin
_
_
_
_
arctan
_
6
8
_
+ 4
5
_
_
_
_
_
_
_
_
1. 5718 + 0. 2034i
z
3
= 10
1/5
_
_
_
_
cos
_
_
_
_
arctan
_
6
8
_
+ 6
5
_
_
_
_
+i sin
_
_
_
_
arctan
_
6
8
_
+ 6
5
_
_
_
_
_
_
_
_
0. 6792 1. 4319i
z
4
= 10
1/5
_
_
_
_
cos
_
_
_
_
arctan
_
6
8
_
+ 8
5
_
_
_
_
+i sin
_
_
_
_
arctan
_
6
8
_
+ 8
5
_
_
_
_
_
_
_
_
1. 1520 1. 0884i
La races son los vrtices de un pntgono regular, como se ve en el siguiente grco.
-2 -1.5 -1 -0.5
0
0.5 1 1.5 2
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0
z
1
z
2
z
3
z
4
z
1. Probar que arg (z
1
/z
2
) = arg (z
1
) arg (z
2
)
2. Probar que si r > 0, entonces arg (rz) = arg (z)
3. Determinar el valor principal de los siguientes nmeros, escriba su forma polar.
(a) 4 + 3i
(b) 1 i
4. Pruebe la identidad de Lagrange:
n
k=0
cos (k) =
1
2
+
sin((n + 1/2) )
2 sin(/2)
Sugerencia. emplear la identidad 1 +z +z
2
+ +z
n
=
1 z
n+1
1 z
y las identidades
cos (x +y) = cos xcos y sinxsiny
cos x cos y = 2
_
sin
1
2
(x +y) sin
1
2
(y x)
_
.
5. Escriba cos (4) y sin(4) en trminos de potencias de cos y sin. Sol. cos (4) = cos
4

6 cos
2
sin
2
+ sin
4
, sin(4) =
_
4 cos
3
sin 4 cos sin
3
_
6. Resolver: z
3
= 8i. Sol.

3 +i,
3 +i, 2i.
7. Calcular
_
1
3i
_
1/2
. Sol.
3 i
2
.
8. Hallar las cuatro races de z
4
+ 1 = 0 y usarlas para factorizar z
4
+ 1. Sol. Races:

2
2
+

2
2
i,
2
2

2
2
i,
2
2
+

2
2
i,
2
2

2
2
i. Factorizacin:
_
z
2
+
2z + 1
_ _
z
2
2z + 1
_
.
9. Hallar las seis races de z
6
+ 1 = 0, Sol.
1
2
3 +
1
2
i,
1
2
3
1
2
i,
1
2
3 +
1
2
i,
1
2
3
1
2
i, i, i.
10. Resolver: z
2
= i, z
2
= i, z
2
=
1
2
i
2
2
. Sol.
2
2
(1 +i) ,
2
2
(1 i) ,
1
2
_
_
3 + 1
_
3 1i
_
11. Resolver:
z
4/3
+ 2i = 0
Sol. 2
3/4
e
i3/8
, 2
3/4
e
i9/8
, 2
3/4
e
i21/8
, 2
3/4
e
i33/8
.
1.5 Conjuntos abiertos y cerrados
Denicin 1.5 (-vecindad)Sea > 0, un conjunto de la forma
V = {z C : |z a| < }
se llama -vecindad de centro a y radio .
a
Denicin 1.6 (Conjunto abierto) Un conjunto A C se dice abierto si para todo a A existe
-vecindad de centro a totalmente contenida en A.
Ejemplo 1.6 Considrese el conjunto
A = {x +iy : x > 0, y > 0, 2x +y < 4}
1.5. CONJUNTOS ABIERTOS Y CERRADOS 23
se puede ver que este conjunto es abierto. Ntese que la regin es el interior de un tringulo, esto
es, no contiene su borde.
x
y
1 2
3
4
1
2
3
4 2 = + y x
Denicin 1.7 (Conjunto cerrado) Un conjunto es cerrado si su complemento es abierto.
Ejercicios
Gracar los siguientes conjuntos indicar si son cerrados o abiertos
1. A = {z : |z i| +|z +i| 1} . Sol. Cerrado
2. A = {x +iy : x > 1, y < 0, x 3y < 1} . Sol. Abierto
3. A = {x +iy : 1 < |z| 4} . Sol. No abierto ni cerrado
4. A = {x +iy : |z| 4, x +y 2} . Sol. Cerrado
Captulo 2
Funciones complejas de variable
compleja
2.1 Funciones
Una funcin de la forma f : D
f
C C se llama funcin compleja de variable compleja, si mediante
la funcin f el nmero complejo x +iy se transforma en u +iv, entonces escribiremos
f (x +iy) = u +iv,
es claro que u y v son funciones reales en las variables x, y, es decir:
u = u(x, y) , v = v (x, y) ,
como es usual D
f
es el dominio de f. Por otra parte el rango de f es el conjunto de todas las
imgenes, esto es, R
f
= {f (z) : z D
f
} .
x
y
u
v
f
Dominio
Rango
y i x +
v i u+
Ejemplo 2.1 Sea f (z) = z
2
, entonces:
f (x +iy) = (x +iy)
2
=
_
x
2
y
2
_
+i (2xy)
25
26 CAPTULO 2. FUNCIONES COMPLEJAS DE VARIABLE COMPLEJA
por tanto:
u(x, y) = x
2
y
2
v (x, y) = 2xy
Ejemplo 2.2 Sea f (z) = |z|
2
, entonces:
f (x +iy) = |x +iy|
2
= x
2
+y
2
luego:
u(x, y) = x
2
+y
2
v (x, y) = 0.
2.2 Transformaciones
Puesto que una funcin compleja f transforma nmeros x +iy en nmeros u +iv, a sta funcin se
llama tambin transformacin o aplicacin.
Ejemplo 2.3 Consideremos la funcin f (z) = z
2
. Determinaremos la regin en el cual se transforma
el conjunto
D = {x +iy : y = x + 1, < x < } ,
para esto ya sabemos que u = x
2
y
2
, v = 2xy. Puesto que y = x + 1 se tiene:
u = x
2
(x + 1)
2
= 2x 1
v = 2x(x + 1) = 2x
2
+ 2x,
de la primera ecuacin se obtiene x =
u + 1
2
, reemplazando en la segunda ecuacin se encuentra:
v = 2
_
u + 1
2
_
2
+ 2
_
u + 1
2
_
=
1
2
_
u
2
1
_
,
es decir: v =
1
2
_
u
2
1
_
. Por otra parte, puesto que < x < ,entonces < 2x 1 < ,es
decir < u < . Por tanto la recta D se transforma en la parbola:
_
u +iv : v =
1
2
_
u
2
1
_
, < u <
_
.
2.2. TRANSFORMACIONES 27
ntese que f (1 + 0i) = 1 y f (0 +i) = 1
x
y
u
1
v
0
1
1 1
1
5 . 1
2 2
1
2
Ejemplo 2.4 Nuevamente consideremos la funcin f (z) = z
2
. Determinaremos la regin del plano
uv en la cual se transforma la franja horizontal:
D = {x +iy : 0 x < , 0 y 1}
que se muestra en la gura:
x
y
3
1
2
1 = y
0 = y
0 = x
1
A
B
O
C
u
v
2 1 0 -1
2
1
para este propsito calcularemos los puntos u+iv en las cuales se transforman los puntos x+iy que
corresponden a las fronteras de la regin D. Recordemos que la transformacin est dada por:
u = x
2
y
2
v = 2xy
Semirecta AB : En este caso y = 1, 0 x < . Empleando la transformacin dada se encuentra:
u = x
2
1
v = 2x,
de donde,
v
2
= 4 (u + 1)
que es una parbola. Puesto que x = v/2 y 0 x < , se deduce 0 v < . esto
da la variacin de v. Para calcular la variacin de u, notemos que si 0 x < , entonces
1 x
2
1 < , puesto que u = x
2
1 se tiene 0 u < .
Semirecta OC : En este caso y = 0, 0 x < . Empleando la transformacin dada se encuentra:
u = x
2
v = 0,
puesto que 0 x < , 0 x
2
< , luego 0 u < , por tanto la semirecta OC se
transforma en la semirecta dada por:
v = 0, 0 u <
Segmento OA : x = 0, 0 y 1. Aplicando la transformacin se encuentra:
u = y
2
v = 0
puesto que 0 y 1, se tiene 1 y
2
0, por tanto 1 u 0, por tanto el segmento
0A se transforma en el segmento dado por:
v = 0, 1 u 0
1. Muestre que f (z) =
1
2
_
z +
1
z
_
transforma la circunferencia |z| = r sobre una elipse con focos
1 y 1 en el plano w.
2. Considere f (z) = z
1
z
, sea D la regin del primer cuadrante entre las circunferencias dadas
por 1 |z| 2. Sol. La cuarta parte de una elipse.
3. Sea f (z) = z
2
. Determinar la regin del plano uv en la cual se transforma la regin:
(a)
D = {x +iy : 0 x 1, 0 y < }
(b) triangular limitada por y = x, x = 1.
Sol. (a) Regin limitada por una parbola y una semirecta en el primer y segundo cuadrantes.
(b) Regin limitada por una parbola y un segmento de recta en el primer y cuarto cuadrantes.
4. Sea f (z) = z +
1
z
. Determinar la regin del plano uv en la cual se transforma la regin:
2.3. LMITES 29
(a) dada por y 0 y |z| 1.
(b) dada por |z| 1
(c) dada por 1 |z| 2 y y 0.
Sol. (a) Semiplano v 0. Sug. La funcin u(x) = x+
1
x
es creciente en los intervalos (, 1)
y (1, ) . (b) Todo el plano. (c) Regin semielipsoidal.
5. Determinar la regin en la cual se convierte
D =
_
x +iy :

2
x , y 2
_
mediante la transformacin f (z) = e
z
. Sol. Cua limitada por dos semicircunferencias y dos
semirectas.
2.3 Lmites
2.3.1 La denicin de lmite
Sea f una funcin de la forma f : D
f
C C, se dice que lim
zz
0
f (z) = w
0
si dado > 0 existe
> 0 tal que
0 < |z z
0
| < entonces |f (z) w
0
| <
que puede interpretar como: si z est cerca de z
0
entonces f (z) est cerca de w
0
. grcamente:
x
y
u
v
0
z
0
w
z
( ) z f
f
Ejemplo 2.5 Probaremos que
lim
z(1+i)
_
z
2
1
_
= 1 + 2i
Hagamos f (z) = z
2
1, z
0
= 1 +i, w
0
= 1 + 2i. Sea > 0, entonces:
|f (z) w
0
| =

(x +iy)
2
1 (1 + 2i)
x
2
y
2
+i (2xy 2)
x
2
y
2
+|2xy 2|
= |(x + 1) (x 1) (y + 1) (y 1)| +|y (x 1) + (y 1)|
< (|x| + 1) |x 1| + (|y| + 1) |y 1| +|y| |x 1| +|y 1|
nos restringimos a los nmeros z del siguiente conjunto
D = {z : |z (1 +i)| < 1} ,
_
vecindad de centro
(1, 1) y radio 1
de esto concluimos que
|x 1| < 1, |y 1| < 1
lo que a su vez signica:
|x| < 2, |y| < 2,
luego:
|f (z) w
0
| < (2 + 1) |x 1| + (2 + 1) |y 1| + 2 |x 1| +|y 1|
= 3 |x 1| + 3 |y 1| + 2 |x 1| +|y 1|
nalmente si |z (1 +i)| < entonces |x 1| < y |y 1| < por tanto_
|f (z) w
0
| < 3 + 3 + 2 + = 9,
De esto deducimos que si = min
_
1,

9
_
se tiene:
|z z
0
| < implica |f (z) w
0
| <
Observacin. Con = 3, se tiene =
1
3
.
Teorema 2.1 (Unicidad del lmite). Si el lmite existe, este es nico.
2.3.2 El lmite de funciones complejas como el lmite de funciones reales
Teorema 2.2 Sea z = x +iy, z
0
= x
0
+iy
0
, y f (z) = u(x, y) +iv (x, y) , entonces:
lim
zz
0
f (z) = u
0
+iv
0
si y solamente si
lim
(x,y)(x
0
,y
0
)
u(x, y) = u
0
y lim
(x,y)(x
0
,y
0
)
v (x, y) = v
0
Este teorema permite el clculo del lmite de una funcin compleja como los lmites de funciones
a varias variables que se estudian en clculo.
Ejemplo 2.6 Calcularemos el lmite:
lim
z(1+i)
_
z
2
1
_
para esto, ntese que f (z) = z
2
1 se escribe como:
f (z) = (x +iy)
2
1
=
_
x
2
y
2
1
_
+i (2xy)
= u(x, y) +iv (x, y) ,
2.3. LMITES 31
puesto que
lim
(x
0
,y
0
)(1,1)
_
x
2
y
2
1
_
= 1
2
1
2
1 = 1
lim
(x
0
,y
0
)(1,1)
(2xy) = 2 (1) (1) = 2
por tanto:
lim
z(1+i)
_
z
2
1
_
= 1 + 2i
2.3.3 Teoremas sobre lmites
Teorema 2.3 Supngase que
lim
zz
0
f (z) = w
0
y lim
zz
0
g (z) = w
1
,
entonces:
lim
zz
0
(f (z) +g (z)) = lim
zz
0
f (z) + lim
zz
0
g (z) = w
0
+w
1
lim
zz
0
(f (z) g (z)) = lim
zz
0
f (z) lim
zz
0
g (z) = w
0
w
1
lim
zz
0
(f (z) g (z)) = lim
zz
0
f (z) lim
zz
0
g (z) = w
0
w
1
lim
zz
0
_
f (z)
g (z)
_
=
lim
zz
0
f (z)
lim
zz
0
g (z)
=
w
0
w
1
, w
1
= 0.
2.3.4 Lmites en el innito
Si al plano complejo se le aade el punto del innito (), este se llama plano complejo exten-
dido. Para precisar este concepto usualmente se emplea la siguiente identicacin. Supngase que
se tiene una esfera y que el plano complejo pasa por su ecuador. Sea N el polo norte, P un punto
de la esfera y z el punto del plano que se obtiene intersectando la recta que para por N y P con
el plano complejo. Se puede ver que a cada punto de la esfera, excepto el punto N, le corresponde
exactamente un punto en el plano complejo, recprocamente, a cada punto del plano complejo le co-
rresponde exactamente un punto de la esfera. Haciendo corresponder el con el punto N tenemos
una correspondencia uno a uno entre la esfera y el plano complejo extendido. La esfera se llama
esfera de Rieman y la correspondencia proyeccin estereogrca.
z
N
P
O
Con la nocin de innito se pueden discutir lmites como:
lim
zz
0
f (z) = o lim
z
f (z) = w
0
El signicado de estos lmites es el siguiente:
lim
zz
0
f (z) = signica que para todo > 0, existe > 0 tal que si 0 < |z z
0
| < ,
entonces
|f (z)| >
1
lim
z
f (z) = w
0
signica que para todo > 0, existe M > 0 tal que si |z| > M entonces
|f (z) w
0
| < .
Propiedad:
lim
zz
0
f (z) = si y solamente si lim
zz
0
1
f (z)
= 0
2.4 Continuidad
Una funcin f (z) es continua en z
0
si:
(a) f (z
0
) existe
(b) lim
zz
0
f (z) = f (z
0
)
Teorema 2.4 Una funcin de variable compleja f (z) es continua en z = x
0
+i y
0
si y solamente si
las funciones u = u(x, y) y v = v (x, y) son continuas en (x
0
, y
0
) , donde f (z) = u(x, y) +i v (x, y) .
Ejemplo 2.7 La funcin f (z) = e
x
y + i
_
x
2
y + cos x
_
es continua en todo el plano complejo pues
u(x, y) = e
x
y y v (x, y) = x
2
y + cos x son continuas en todo (x, y) R
2
.
2.5 Derivadas
2.5.1 La denicin de derivada
Sea f una funcin denida en un intervalo abierto U. La derivada de f en z U, denotada por
f
(z) , es
lim
h0
f (z +h) f (z)
h
siempre que tal lmite exista.
Ejemplo 2.8 Sea f (z) = z
3
. entonces:
f
(z) = lim
h0
f (z +h) f (z)
h
= lim
h0
(z +h)
3
z
3
h
= lim
h0
(z +h)
3
z
3
h
= lim
h0
3z
2
h + 3zh
2
+h
3
h
= lim
h0
_
3z
2
+ 3zh +h
2
_
= 3z
2
2.5. DERIVADAS 33
Observacin. Si f
(z) existe, se dir que f es diferenciable en z, ms an si f
(z) existe para

todo z A, se dir que f es diferenciable en A.
2.5.2 Teoremas sobre la derivada
Teorema 2.5 Sean f, g funciones diferenciables en z y c una constante, entonces:
(c)
= 0
(z
n
)
= nz
n1
(f (z) +g (z))
= f
(z) +g
(z)
(f (z) g (z))
= f
(z) g
(z)
(f (z) g (z))
= f
(z) g (z) +f (z) g
(z)
_
f (z)
g (z)
_
=
f
(z) g (z) f (z) g
(z)
(g (z))
2
, g (z) = 0
Teorema 2.6 (Regla de la cadena) Si g es diferenciable en z y f es diferenciable en g (z) ,
entonces la funcin compuesta f g es diferenciable en z, ms an
(f g)
(z) = f
(g (z)) g
(z) .
2.5.3 Las ecuaciones de Cauchy-Rieman
Sea f (x +iy) = u(x, y) +iv (x, y) , las ecuaciones:
u
x
=
v
y
u
y
=
v
x
se llaman ecuaciones de Cauchy-Rieman.
El siguiente teorema es una condicin necesaria pero no suciente para la existencia de la derivada
de una funcin. Su forma contrapositiva nos permite descubrir los puntos donde una funcin no es
diferenciable.
Condicin necesaria para la existencia de la derivada
Teorema 2.7 Sea f (x +iy) = u(x, y) + iv (x, y) . Supngase que f
(x
0
+iy
0
) existe, entonces las
primeras derivadas parciales de u y v satisfacen las ecuaciones de Cauchy-Rieman en (x
0
, y
0
) . Ms
an, en este caso:
f
(x
0
+iy
0
) =
u(x
0
, y
0
)
x
+i
v (x
0
, y
0
)
x
.
Observacin. En su forma contrapositiva, el teorema anterior dira:
Si las ecuaciones de Cauchy-Rieman no se cumplen
en (x
0
, y
0
) entonces f
(x
0
+iy
0
) no existe.
Ejemplo 2.9 Considere la funcin f (z) = z
3
. Observemos que
f (z) = (x iy)
3
=
_
x
3
3xy
2
_
+i
_
3x
2
y +y
3
_
de donde u(x, y) = x
3
3xy
2
y v (x, y) = 3x
2
y +y
3
.
u
x
= 3x
2
3y
2
,
v
y
= 3x
2
+ 3y
2
,
u
y
= 6xy,
v
x
= 6xy
por tanto no se cumplen las ecuaciones de Cauchy-Rieman salvo para x = y = 0. Luego f (z) = z
3
no es diferenciable en ningn punto distinto de cero.
Condicin suciente para la existencia de la derivada
Teorema 2.8 Sea f (x +iy) = u(x, y)+iv (x, y) denida en un vecindad de x
0
+iy
0
. Supngase
que:
1. las primeras derivadas parciales de u y v existen en toda la vecindad y son continuas en
(x
0
, y
0
) .
2. las ecuaciones de Cauchy- Rieman se satisfacen en (x
0
, y
0
) .
Entonces f
(x
0
+iy
0
) existe.
Ejemplo 2.10 Consideremos nuevamente la funcin f (z) = z
3
=
_
x
3
3xy
2
_
+ i
_
3x
2
y +y
3
_
,
claramente las primeras derivadas parciales de u y v existen en todas partes, ms an son continuas,
adems las derivadas satisfacen las ecuaciones de Cauchy-Rieman en 0+0i, entonces f es diferenciable
en z = 0 + 0i, nalmente:
f
(0 + 0i) =
u(0, 0)
x
+i
v (0, 0)
x
= 0 +i0
1. En las siguientes funciones, determine los puntos z en donde la condicin necesaria de existencia
de la derivada muestra que f
(z) no existe.
(a) f (z) = z + 2 3i. Sol. C
2.6. FUNCIONES ANALTICAS, ENTERAS Y ARMNICAS 35
(b) f (z) = e
x+2
+iy. Sol. C
(c) f (z) = e
x
(cos y +i siny) . Sol.
(d) f (z) = 2x
2
y +i2xy
2
. Sol. C{0 + 0i}
(e) f (z) = |z|
2
. Sol. C{0 + 0i}
(f) f (z) = 2x
5
+i (1 2y)
5
. Sol. C{i/2}
2. Emplear las condiciones necesarias y sucientes para determinar la derivada de las siguientes
funciones en los puntos en donde exista.
(a) f (z) = |z|
2
. Sol. f
(0 + 0i) = 0
(b) f (z) =
1
z 3i
. Sol. f
(z) =
1
(z 3i)
2
, z = 3i.
(c) f (z) = e
3x+3iy
. Sol. f
(z) = 3e
3x
cos 3y +i3e
3x
sin3y = 3e
3x+i3y
(d) f (z) = (Re z + 2)
2
+i (Imz + 4)
2
. Sol. f
(z) = 2 (x + 2) , en el conjunto {z = x +iy : y = x 2}

2.6 Funciones analticas, enteras y armnicas
2.6.1 Funciones analticas
Denicin 2.9 (Funcin analtica) Una funcin es analtica en un conjunto abierto U si tiene
derivada en todo punto de ese conjunto. La funcin es analtica en un punto si es analtica en un
conjunto abierto que contiene el punto.
Ejemplo 2.11 f (z) =
1
zi
es analtica en todo z = i.
Ejemplo 2.12 f (z) = |z|
2
no es analtica en ningn punto.
2.6.2 Funciones enteras
Denicin 2.10 (Funcion entera) Una funcin es entera si es analtica en todo el plano complejo.
Ejemplo 2.13 Todo polinomio es una funcin entera.
Denicin 2.11 (Punto singular) Si una funcin no es analtica en un punto z
0
, pero analtica
en una vecindad de z
0
, se dir que z
0
es un punto singular de f.
Ejemplo 2.14 f (z) =
1
z
2
+ 1
tiene puntos singulares en z = i.
2.6.3 Funciones armnicas
Denicin 2.12 (Funcin armnica) Una funcin real (x, y) es armnica en algn dominio si
se satisface la ecuacin de Laplace:
2
(x, y)
x
2
+

2
(x, y)
y
2
= 0.
es usual denir el operador de Laplace como
=
_

x
_
2
+
_

y
_
2
,
entonces la ecuacin de Laplace toma la forma:
= 0
Teorema 2.13 La parte real y la parte compleja de una funcin analtica son armnicas.
Ejemplo 2.15 Considere f (z) =
1
z
, esta funcin es analtica en todo z = 0 + 0i.
f (z) =
1
x +iy
=
x iy
x
2
+y
2
=
x
x
2
+y
2
+i
y
x
2
+y
2
por tanto para (x, y) = (0, 0) , las funciones
u(x, y) =
x
x
2
+y
2
v (x, y) =
y
x
2
+y
2
deben ser armnicas, en efecto:
u(x, y)
x
=
x
2
y
2
(x
2
+y
2
)
2
,

2
u(x, y)
x
2
=
2x
_
x
2
3y
2
_
(x
2
+y
2
)
3
u(x, y)
y
=
2xy
(x
2
+y
2
)
2
,

2
u(x, y)
y
2
=
2x
_
x
2
3y
2
_
(x
2
+y
2
)
3
luego:
2
u(x, y)
x
2
+

2
u(x, y)
y
2
= 0.
La prueba de que v es armnica es anloga.
Denicin 2.14 (Armnica conjugada) Sean u y v funciones armnicas en un dominio D tales
que sus derivadas parciales satisfacen las ecuaciones de Cauchy-Rieman.en el dominio D, en tal caso
diremos v es armnica conjugada de u.
Observacin. La propiedad ser armnica conjugada no es conmutativa, es decir, si v es armnica
conjugada de u, no es cierto, en general, que u sea armnica conjugada de v.
Teorema 2.15 Sea f (z) = u(x, y) + iv (x, y) . f es analtica en un dominio D si y solamente si v
es armnica conjugada de u.
Es posible determinar la armnica conjugada a partir de una armnica dada.
2.6. FUNCIONES ANALTICAS, ENTERAS Y ARMNICAS 37
Ejemplo 2.16 Sea u(x, y) = 3xy, claramente es armnica. Si v es armnica conjugada de u,
entonces
u
x
=
v
y
y
u
y
=
v
x
entonces:
v
y
= 3y ...................................(1)
v
x
= 3x ...................................(2)
de (1) v (x, y) =
3
2
y
2
+g (x) , combinando este resultado con (2) se encuentra:
g
(x) = 3x
de donde g (x) =
3
2
x
2
+C. Por tanto
v (x, y) =
3
2
y
2
3
2
x
2
+C
es la armnica conjugada de u(x, y) .
Observacin. Ntese que con x =
1
2
(z +z) y y =
1
2i
(z z) entonces la funcin
f (z) = u(x, y) +iv (x, y)
= 3xy +i
3
2
_
y
2
x
2
_
=
3
4i
(z +z) (z z) +i
3
8
_
(z z)
2
(z +z)
2
_
=
3
4i
_
z
2
z
2
_
+i
3
8
_
z
2
+ 2zz z
2
z
2
2zz z
2
_
= i
3
4
_
z
2
z
2
_
i
3
4
_
z
2
+z
2
_
= i
3
2
z
2
es analtica.
1. Sea =
_

x
_
2
+
_

y
_
2
. Pruebe que
= 4

z

z
2. Encuentre una funcin analtica cuya parte real es
(a) u(x, y) = 3x
2
y y
3
. Sol. v = 3xy
2
x
3
.
(b) u(x, y) = x +
x
x
2
+y
2
. Sol. v = y +
y
x
2
+y
2
.
(c) u(x, y) = x xy. Sol. v = y
1
2
y
2
+
1
2
x
2
.
(d) u(x, y) = ln
_
x
2
+y
2
_
. Sol. v = 2 arctan
_
y
x
_
.
(e) u(x, y) = 2x(1 y) . Sol. v = x
2
y
2
+ 2y.
(f) u(x, y) = 2x x
3
+ 3xy
2
. Sol. v = 2y 3x
2
y +y
3
.
2.7 Funciones elementales
2.7.1 Funcin exponencial
Se dene por f (z) = e
z
. Ntese que
f (x +iy) = e
x
(cos y +i siny)
Propiedades.
1. Para todo z complejo:
d
dz
e
z
= e
z
2. La funcin exponencial es entera
3. Si z
1
y z
2
son nmeros complejos:
e
z
1
+z
2
= e
z
1
e
z
2
4. La funcin exponencial es peridica de periodo 2i, es decir:
e
z+2i
= e
z
5. Si z = x +iy, |e
z
| = e
x
, arg(e
z
) = y + 2k, k = 0, 1, 2, . . . , ms an, e
z
= 0 para todo z.
6. Las soluciones de
e
z
= e
i
son:
z = ln +i ( + 2k) , k = 0, 1, 2, . . .
2.7. FUNCIONES ELEMENTALES 39
1. Probar las anteriores propiedades.
2. Probar: e
2+3i
4
=
_
e
2
_
1
2
(1 +i)
3. Resolver:
(a) e
z
= 9. Sol. ln9 +i (1 + 2k) , k = 0, 1, 2, . . .
(b) e
z
= 1 +
3 i. Sol. ln2 +i
_
1
3
+ 2k
_
, k = 0, 1, 2, . . .
(c) e
2z1
= 1. Sol.
1
2
+ki, k = 0, 1, 2, . . .
4. Probar que
(a) e
z
= e
z
(b) e
iz
= e
iz
si y solamente si z = k, k = 0, 1, 2, . . .
(c) Si e
z
es real entonces Imz = k, k = 0, 1, 2, . . .
5. Cuando e
z
es imaginario puro?
6. Pruebe que e
z
no es analtica en ningn punto.
2.7.2 Funciones trigonomtricas
Se denen como:
sinz =
1
2i
_
e
iz
e
iz
_
cos z =
1
2
_
e
iz
+e
iz
_
tanz =
sinz
cos z
cot z =
cos z
sinz
sec z =
1
cos z
csc z =
1
sinz
Propiedades
1. sin(z) = sinz
2. cos (z) = cos z
3. Empleando las deniciones de las funciones hiperblicas
sinht =
1
2
_
e
t
e
t
_
cosht =
1
2
_
e
t
+e
t
_
se puede probar:
(a) sin(iy) = i sinhy
(b) cos (iy) = coshy
4. sinz y cos z son enteras, sus derivadas son
d
dz
sinz = cos z,
d
dz
cos z = sinz
5. Se satisfacen adems otras propiedades usuales.
(a) sin(z
1
+z
2
) = sinz
1
cos z
2
+ cos z
1
sinz
2
(b) cos (z
1
+z
2
) = cos z
1
cos z
2
sinz
1
sinz
2
(c) sin
2
z + cos
2
z = 1
(d) sin2z = 2 sinz cos z
(e) cos 2z = cos
2
z sin
2
z
(f) sin(z +/2) = cos z
(g) sin(z + 2) = sinz
(h) cos (z + 2) = cos z
(i) sin(z +) = sinz
(j) cos (z +) = cos z
(k) 2 sinz
1
cos z
2
= sin(z
1
+z
2
) + sin(z
1
z
2
)
6. sinz = sinxcoshy +i cos xsinhy
7. cos z = cos z coshy i sinxsinhy
2.7.3 Funciones hiperblicas
Se denen:
sinhz =
1
2
(e
z
e
z
)
coshz =
1
2
(e
z
+e
z
)
tanhz =
sinhz
coshz
cothz =
1
tanhz
sechz =
1
coshz
cschz =
1
sinhz
1. Probar las anteriores propiedades
2. Resolver:
(a) sinz = cosh4. Sol.
_
2k +
1
2
_
4i, k = 0, 1, 2, . . .
(b) sin2z = 2
(c) cos z = 2, Sol. 2k i ln
_
2 +
3
_
(d) sinz = 4, Sol. z =
_
2
+ 2k
_
i ln
_
4
15
_
2.7. FUNCIONES ELEMENTALES 41
(e) cos 3z = 9
3. Probar que
(a) i sinh(iz) = sinz
(b) i sin(iz) = sinhz
(c) cos (iz) = coshz
(d) sinh(z) = sinhz
(e) cosh(iz) = coshz
(f) sinh(z
1
+z
2
) = sinhz
1
coshz
2
+ coshz
1
sinhz
2
(g) cosh(z
1
+z
2
) = coshz
1
coshz
2
+ sinhz
1
sinhz
2
4. Resolver
(a) cosh(z) = 1/2, Sol.
_
2k
1
3
_
i
(b) cosh(4z) = 1/2,
(c) sinh(2z) = i, Sol. i
_
4
+k
_
, k Z
Captulo 3
Anlisis de Fourier
3.1 Aspectos bsicos de la serie de Fourier
3.1.1 Introduccin
Funciones peridicas
Se dice que una funcin f (x) es peridica si existe un nmero P tal que f (x +P) = f (x) , el nmero
P ms pequeo que satisface esta propiedad se llama periodo. Es claro que para todo entero n se
cumple f (x +nP) = f (x) .
x
y
Periodo
Ejemplo 3.1 Son funciones peridicas, de periodo 2, las funciones cos (x) y sin(x) .
Extensin peridica
Denicin 3.1 (Extensin peridica) Considrese una funcin f denida en [L, L] , denimos
su extensin peridica tomando la grca de f en [L, L) y repitindola en cada intervalo de longitud
2L, la funcin f
P
denida de esta manera cumple f
P
(x + 2L) = f
P
(x) para todo x R, la funcin
f
P
es peridica de periodo 2L.
Ejemplo 3.2 Si f (x) = (x 1)
3
(x 1) , x [0, 2.5] , la grca y su extensin peridica se
43
44 CAPTULO 3. ANLISIS DE FOURIER
muestran a continuacin.
0
1
2
1 2 2.5
y
( ) ( ) ( ) 1 1
3
= x x x f
0
1
2
1 2 2.5 3.5 4.5 5 -1.5 -0.5
y
x
Funcin extendida peridicamente
Ejercicios
1. Determinar los periodos de las siguientes funciones:
(a) f (x) = sin(ax) . Sol. 2/a.
(b) f (x) = sin(8x + 4) .
(c) f (x) = sin(6x) + sin(8x) . Sol.
(d) f (x) = sin(3x) + sin(5x) .
(e) f (x) = sin
_
3
2
x
_
+ 2 cos
_
5
3
x
_
. Sol. 12
(f) f (x) = sin(1.4x) + 5 sin(0.2x) + cos (4x)
2. Prubese que si f es funcin par entonces:
_
P
P
f (x) dx = 2
_
P
0
f (x) dx y si f es impar:
_
P
P
f (x) dx = 0.
3. Si f es peridica de periodo P, entonces para todo nmero a :
_
P
0
f (x) dx =
_
P+a
a
f (x) dx
4. Sea P el periodo de f (x) = cos (ax) + sin(bx) , probar que existen enteros m, n tales que
a
b
=
m
n
.
5. Pruebe que f (x) = cos (t) + sin(1 +) t no es peridica. (Sug. Emplee la conclusin del
ejercicio anterior)
3.1. ASPECTOS BSICOS DE LA SERIE DE FOURIER 45
Ortogonalidad de funciones exponenciales complejas
Teorema 3.2 Considrese el conjunto
_
e
i2nx/P
: n entero
_
,
entonces se verica:
1
P
_
P
0
e
i2mx/P
e
i2nx/P
dx =
_
0 m = n
1 m = n
Demostracin. Si n = m, entonces:
1
P
_
P
0
e
i2mx/P
e
i2nx/P
dx =
1
P
_
P
0
e
i2(mn)x/P
dx
=
1
P
P
i2 (mn)
e
i2(mn)x/P
P
0
=
1
i2 (mn)
_
e
i2(mn)
1
_
= 0
Si m = n :
1
P
_
P
0
e
i2mx/P
e
i2nx/P
dx =
1
P
_
P
0
dx = 1.
Ortogonalidad de las funciones seno y coseno

Ntese que:
e
i2mx/P
e
i2nx/P
=
_
cos
2mx
P
+i sin
2mx
P
__
cos
2nx
P
i sin
2nx
P
_
= cos
2mx
P
cos
2nx
P
+ sin
2mx
P
sin
2nx
P
+i
_
sin
2mx
P
cos
2nx
P
cos
2mx
P
sin
2nx
P
_
,
esto motiva el clculo de las siguientes integrales:
1
P
_
P
0
_
cos
2mx
P
cos
2nx
P
_
dx
1
P
_
P
0
_
sin
2mx
P
sin
2nx
P
_
dx
1
P
_
P
0
_
sin
2mx
P
cos
2nx
P
_
dx
1
P
_
P
0
_
cos
2mx
P
sin
2nx
P
_
dx
un clculo elemental da:
2
P
_
P
0
_
cos
2mx
P
cos
2nx
P
_
dx =
_
0 n = m
1 n = m
2
P
_
P
0
_
sin
2mx
P
sin
2nx
P
_
dx =
_
0 n = m
1 n = m
1
P
_
P
0
_
sin
2mx
P
cos
2nx
P
_
dx = 0, para todo m, n
que puede escribirse tambin como:
_
P
0
_
cos
2mx
P
cos
2nx
P
_
dx =
_
0 n = m
P
2
n = m
_
P
0
_
sin
2mx
P
sin
2nx
P
_
dx =
_
0 n = m
P
2
n = m
_
P
0
_
sin
2mx
P
cos
2nx
P
_
Observacin. La propiedad de ortogonalidad de las anteriores funciones se extiende a cualquier
intervalo [d, d +P], es decir:
1
P
_
d+P
d
e
i2mx/P
e
i2nx/P
dx =
_
0 m = n
1 m = n
_
d+P
d
_
cos
2mx
P
cos
2nx
P
_
dx =
_
0 n = m
P
2
n = m
_
d+P
d
_
sin
2mx
P
sin
2nx
P
_
dx =
_
0 n = m
P
2
n = m
_
d+P
d
_
sin
2mx
P
cos
2nx
P
_
En efecto: Si m = n :
1
P
_
d+P
d
e
i2mx/P
e
i2nx/P
dx =
1
P
_
d+P
d
e
i2(mn)x/P
dx
=
1
P
P
i2 (mn)
e
i2(mn)x/P
d+P
d
=
1
i2 (mn)
_
e
i2(mn)(d+P)/P
e
i2(mn)d/P
_
=
1
i2 (mn)
_
e
i2(mn)d/P
e
i2(mn)
e
i2(mn)d/P
_
=
1
i2 (mn)
_
e
i2(mn)d/P
e
i2(mn)d/P
_
= 0
3.2. LA SERIE DE FOURIER DE UNA FUNCIN 47
Si n = m :
1
P
_
d+P
d
e
i2mx/P
e
i2nx/P
dx =
1
P
_
d+P
d
dx
= 1
la demostracin es anloga para las funciones seno y coseno.
3.2 La serie de Fourier de una funcin
Supngase que f es una funcin denida en [L, L], supngase existen nmeros a
n
y b
n
tales que:
f (x) =
1
2
a
0
+

n=1
a
n
cos
_
nx
L
_
+b
n
sin
_
nx
L
_
para x [L, L] , ms adelante justicaremos este hecho.
3.2.1 Clculo de las constantes a
n
, b
n
.
Aplicaremos las propiedades de las integrales de seno y coseno antes mencionadas. Con P = 2L y
d = L se encuentra:
_
L
L
_
cos
mx
L
cos
nx
L
_
dx =
_
0 n = m
L n = m
_
L
L
_
sin
mx
L
sin
nx
L
_
dx =
_
0 n = m
L n = m
_
L
L
_
sin
mx
L
cos
nx
L
_
ms an:
_
L
L
cos
_
mx
L
_
dx =
_
L
L
sin
_
mx
L
_
dx = 0.
Clculo de a
0
. Integramos f (x)
_
L
L
f (x) dx =
_
L
L
_
1
2
a
0
+

n=1
a
n
cos
_
nx
L
_
+b
n
sin
_
nx
L
_
_
dx
=
_
L
L
1
2
a
0
dx
= La
0
de donde:
a
0
=
1
L
_
L
L
f (x) dx.
Clculo de a
n
(n 1). Integramos f (x) cos
_
nx
L
_
(ntese que precisamente cos
_
nx
L
_
es el
coeciente de a
n
)
_
L
L
f (x) cos
_
nx
L
_
dx =
_
L
L
_
1
2
a
0
+

m=1
a
m
cos
_
mx
L
_
+b
m
sin
_
mx
L
_
_
cos
_
nx
L
_
dx
=

m=1
a
m
_
L
L
cos
_
mx
L
_
cos
_
nx
L
_
dx +
m=1
b
m
_
L
L
sin
_
mx
L
_
cos
_
nx
L
_
dx
= La
n
luego:
a
n
=
1
L
_
L
L
f (x) cos
_
nx
L
_
dx, n = 1, 2, . . .
sta frmula es vlida para n = 0. {Esto justica la eleccin de a
0
= 2A
0
}
Clculo de b
n
. Integramos f (x) sin
_
nx
L
_
(nuevamente ntese que sin
_
nx
L
_
es el coeciente
de b
n
)
_
L
L
f (x) sin
_
nx
L
_
dx =
_
L
L
_
1
2
a
0
+

m=1
a
m
cos
_
mx
L
_
+b
m
sin
_
mx
L
_
_
sin
_
nx
L
_
dx
=

m=1
a
m
_
L
L
cos
_
mx
L
_
sin
_
nx
L
_
dx +
m=1
b
m
_
L
L
sin
_
mx
L
_
sin
_
nx
L
_
dx
= Lb
n
luego:
b
n
=
1
L
_
L
L
f (x) sin
_
nx
L
_
dx, n = 1, 2, . . .
De todo lo anterior deducimos que una funcin f se expresa como:
f (x) =
1
2
a
0
+

n=1
_
a
n
cos
nx
L
+b
n
sin
nx
L
_
donde:
a
n
=
1
L
_
L
L
f (x) cos
_
nx
L
_
dx, n = 0, 1, 2, . . .
b
n
=
1
L
_
L
L
f (x) sin
_
nx
L
_
dx, n = 1, 2, . . .
Observacin importante: los resultados obtenidos siguen siendo vlidos en cualquier intervalo
de longitud P de la forma [d, d +P] , en tal caso tendremos:
f (x) =
1
2
a
0
+

n=1
_
a
n
cos
2nx
P
+b
n
sin
2nx
P
_
donde:
a
n
=
2
P
_
d+P
d
f (x) cos
_
2nx
P
_
dx, n = 0, 1, 2, . . .
b
n
=
2
P
_
d+P
d
f (x) sin
_
2nx
P
_
dx, n = 1, 2, . . .
Con d = L y P = 2L tendremos los anteriores resultados.
Ejemplo 3.3 Determinaremos la serie de Fourier de la funcin f (x) = |x| , x [, ] .
a
0
=
1
|x| dx
=
1
__
0
xdx +
_

0
xdx
_
=
1
1
2
x
2
+
1
2
x
2
0
_
=
1
_
1
2
2
+
1
2
2
_
=
a
n
=
1
|x| cos
nx
dx
=
1
__
0
(xcos nx) dx +
_

0
(xcos nx) dx
_
=
2 (1 + (1)
n
)
n
2
b
n
=
1
|x| sin
nx
dx
=
1
__
0
(xsinnx) dx +
_

0
(xsinnx) dx
_
= 0
por tanto la serie de Fourier de f (x) es:
1
2
+

n=1
_
2 (1 + (1)
n
)
n
2
_
cos nx
Ms adelante justicaremos porqu podemos escribir:
f (x) =
1
2
+

n=1
_
2 (1 + (1)
n
)
n
2
_
cos nx, x [, ] ,
al respecto, debemos dejar en claro los siguientes aspectos:
Observacin 1. x debe estar en el intervalo [, ] , cuando esto no ocurre la igualdad carece
de sentido, a continuacin se muestra un cuadro para ver esta situacin:
x
1
2
+

n=1
_
2 (1 + (1)
n
)
n
2
_
cos nx f (x)
0.5 0.50003 9 0.5
1.0 1.00003 9 1.0
1.5 1.50004 6 1.5
4.0 2.28311 5 4
4.0 2 2.28311 5 2. 28318 5
notemos que evidentemente f (x) =
1
2
+

n=1
_
2 (1 + (1)
n
)
n
2
_
cos nx para x [, ] pero no
fuera de este intervalo, sin embargo, la serie tiene las mismas imgenes en 4 y 4 2, ms adelante
justicaremos que en realidad la serie es peridica, de periodo 2.
Observacin 2. En la prctica, la suma innita nunca puede realizarse, lo usual es realizar la
siguiente aproximacin:
f (x)
1
2
+
N
n=1
_
2 (1 + (1)
n
)
n
2
_
cos nx, x [, ] ,
a continuacin mostramos las grcas para algunos valores de N comparadas con la grca de |x|
en [, ] .
x
4 2 0 -2 -4
2.5
2
1.5
1
0.5
x
4 2 0 -2 -4
3
2.5
2
1.5
1
0.5
x
4 2 0 -2 -4
3
2.5
2
1.5
1
0.5
0
x
4 2 0 -2 -4
3
2.5
2
1.5
1
0.5
0
1 = N
51 = N 11 = N
3 = N
Ejemplo 3.4 Consideremos ahora f (x) = x, denida en [, ].
a
0
=
1
xdx
= 0
a
n
=
1
(xcos (nx) ) dx
= 0
b
n
=
1
(xsin(nx) ) dx
=
1
(xsin(nx) ) dx
=
1
_
sinnx nxcos nx
n
2
_
=
1
_
n cos (n)
n
2

+n cos (n)
n
2
_
=
2 (1)
n+1
n
, {Ntese que cos (n) = (1)
n
}
por tanto su serie de Fourier es;
f (x) =

n=1
2 (1)
n+1
n
sin(nx)
Con 20 trminos de la serie se tiene: f (x) =
20
n=1
2 (1)
n+1
n
sin(nx)
4 2 0 -2 -4
3
2
1
0
-1
-2
-3
x
y

Con 50: f (x) =
50
n=1
2 (1)
n+1
n
sin(nx)
3 2 1 0
-
1
-
2
-
3
3
2
1
0
-
1
-
2
-
3
x
y

Ejemplo 3.5 Considere la funcin f (x) = x
2
x, denida en [0, 1], determinaremos su serie de
Fourier. Notemos que en este caso P = 1.
Clculo de a
0
:
a
0
=
2
1
_
1
0
_
x
2
x
_
dx
=
1
3
Clculo de a
n
.
a
n
=
2
1
_
1
0
__
x
2
x
_
cos (2nx)
_
dx
=
1
2
2
n
2
_
4
2
n
2
x
2
sin2nx 2 sin2nx + 4nxcos 2nx
_
1
2n
(cos 2nx + 2nxsin2nx)
2n
1
0
=
1
2
2
n
2
(4n)
1
2n
(1)
2n

1
2n
(1)
2n
=
1
2
n
2
Clculo de b
n
.
b
n
=
2
1
_
1
0
__
x
2
x
_
sin(2nx)
_
dx
=
1
4
2
n
2
_
4
2
n
2
x
2
cos 2nx + 2 cos 2nx + 4nxsin2nx
_
1
2n
(sin2nx 2nxcos 2nx)
n
1
0
=
1
4
2
n
2
_
4
2
n
2
+ 2
_
1
2n
(2n)
n

1
4
2
n
2
(2)
1
2n
(2n)
n
=
nsin2n + cos 2n 1
2
3
n
3
= 0
Por tanto:
f (x) =
1
2
a
0
+

n=1
a
n
cos (nx) +b
n
sin(nx)
=
1
2
a
0
+

n=1
a
n
cos (2nx) +b
n
sin(2nx)
=
1
6
+

n=1
cos (2nx)
2
n
2
Con dos armnicos se encuentra:
f (x)
1
6
+
2
n=1
cos (2nx)
2
n
2
2
0
-1
-2
0.4
0.2
0
-0.2
-0.4
x
y
1
y con 20 armnicos: f (x, 20) =
1
6
+
20
n=1
cos (2nx)
2
n
2
x
y
2
1
0
-1
-2
0.4
0.2
0
-0.2
-0.4
Ejercicios
Hallar las series de Fourier de las siguientes funciones. Suponga que se extiende peridicamente en
R.
1.
f (x) =
_
0 para x [3, 0]
x para x [0, 3]
Sol.
3
4
+

n=1
_
3
n
2
2
[(1)
n
1] cos
_
nx
3
_
+
3
n
(1)
n+1
sin
_
nx
3
_
_
.
2. f (x) = e
4x
, x [2, 2] .
Sol. a
0
=
1
8
_
e
8
e
8
_
, a
n
=
_
e
8
e
8
_
8(1)
n
64+
2
n
2
, b
n
=
_
e
8
e
8
_
n(1)
n
64+
2
n
2
3. f (x) = |sinx| , x [, ]
4. f (x) = x
2
2x, denida en (0, 2) .
(a) Sol. a
0
=
4
3
, a
n
=
4
2
n
2
, b
n
= 0, n 1.
5. f (x) = x
2
+ 2x en (0, 2)
(a) Sol.
2
3
+

n=1
_
4n
3
n
3
cos (nx)
_
6. f (x) =
_
x (0, 1)
x + 1 (1, 2)
en (0, 2)
(a) Sol. f (x) =

n=1
_
_
2
(1)
n
1
2
n
2
_
cos (nx) +
_
1 (1)
n
n
_
sin(nx)
_
7. f (x) =
_
0 x (5, 0)
3 x (0, 5)
(a) Sol.
3
2
+

n=1
3(1cos n)
n
sin
nx
5
8. f (x) = x
2
denida en (0, 2) .
(a) Sol.
4
2
3
+

n=1
_
4
n
2
cos nx
4
n
sinnx
_
9. Sea f (x) = cos (ax) donde a
2
no es entero y x [, ] . Halle su serie de Fourier y luego
probar:
sin(a)
= 2a
_
1
2a
2

1
a
2
1
2
+
1
a
2
2
2
+
1
a
2
3
2
+
_
3.3. SERIES DE FOURIER EN SENOS Y COSENOS 55
3.3 Series de fourier en senos y cosenos
Si una funcin tiene algunas propiedades de simetra, las frmulas para los coecientes de Fourier
tienen algunas simplicaciones.
Denicin 3.3 (Funcin par e impar) Sea f una funcin denida en (L, L) . Si f (x) = f (x)
para todo x (L, L) , f se llama funcin par. Si f (x) = f (x) para todo x (L, L) , f se
llama funcin impar.
La propiedad fundamental de estas funciones se presenta en el siguiente resultado.
Teorema 3.4 Si f es una funcin par en (L, L), entonces:
_
L
L
f (x) dx = 2
_
L
0
f (x) dx
Teorema 3.5 Si f es una funcin impar en (L, L), entonces:
_
L
L
f (x) dx = 0
Adems:
Teorema 3.6 El producto de funciones pares e impares satisface:
funcin f funcin g funcin fg
par par par
par impar impar
impar par impar
impar impar par
3.3.1 El caso de una funcin par
Supngase que f es una funcin par en (L, L). Los coecientes de Fourier son
a
n
=
2
2L
_
L
L
f (x) cos
_
2nx
2L
_
dx
=
2
L
_
L
0
f (x) cos
_
nx
L
_
dx, n = 0, 1, 2, . . .
b
n
=
2
2L
_
L
L
f (x) sin
_
nx
L
_
dx = 0, n = 1, 2, . . .
Ejemplo 3.6 En el ejemplo 3.3 pgina 49 Se a calculado la serie de Fourier de la funcin f (x) = |x| ,
x [, ] .
a
0
=
a
n
=
2 (1 + (1)
n
)
n
2
b
n
= 0
por tanto la serie de Fourier de f (x) es:
1
2
+

n=1
_
2 (1 + (1)
n
)
n
2
_
cos nx
3.3.2 El caso de una funcin impar
Supngase que f es una funcin impar en (L, L). Los coecientes de Fourier son
a
n
=
2
2L
_
L
L
f (x) cos
_
2nx
2L
_
dx = 0, n = 0, 1, 2, . . .
b
n
=
2
L
_
L
L
f (x) sin
_
nx
L
_
dx
=
2
L
_
L
0
f (x) sin
_
nx
L
_
dx, n = 1, 2, . . .
Ejemplo 3.7 En la pgina 50, ejercicio 3.4 se ha calculado la serie de Fourier de f (x) = x, denida
en [, ].
a
0
= 0
a
n
= 0
b
n
=
2 (1)
n+1
n
,
por tanto su serie de Fourier es:
n=1
2 (1)
n+1
n
sin(nx)
3.3. SERIES DE FOURIER EN SENOS Y COSENOS 57
3.3.3 Desarrollo de una funcin en senos y cosenos
Si una funcin f est denida en el intervalo (0, L) , entonces:
(a) la serie de Fourier en cosenos est dado por
f (x) =
1
2
a
0
+

n=1
a
n
cos
_
nx
L
_
donde
a
n
=
2
L
_
L
0
f (x) cos
_
nx
L
_
dx, n = 0, 1, 2, . . .
(b) la serie de Fourier en senos est dado por:
f (x) =

n=1
b
n
sin
_
nx
L
_
donde
b
n
=
2
L
_
L
0
f (x) sin
_
nx
L
_
dx, n = 0, 1, 2, . . .
Ejercicios
1. Desarrollar las siguientes funciones en trminos de (i) senos y (ii) cosenos
(a) f (x) = 1 en (0, 1)
Sol. (i)

n=0
4 sin((2n + 1) x)
(2n + 1)
(que es igual a

n=1
2 (1 (1)
n
) sin(nx)
n
), (ii) 1
(b) f (x) = sinx en (0, /2).
Sol. (i)

n=1
_
8 (1)
n
n
(4n
2
1)
_
sin(2nx), (ii)
2
n=1
4 cos (2nx)
(4n
2
1)
(c) f (x) =
_
x x (0, 4)
8 x x (4, 8)
Sol. (i)
32
n=1
_
1
n
2
sin
n
2
sin
nx
8
_
,
(ii 2 +
16
n=1
_
1
n
2
_
(1)
n+1
1 + 2 cos
n
2
_
cos
nx
8
_
2. Demostrar que para 0 x :
(a) x( x) =

2
6

n=1
cos (2nx)
n
2
(b) x( x) =
8
n=1
sin((2n 1) x)
(2n 1)
3
3. Use el anterior problema para probar:
n=1
1
n
2
=

2
6
,

n=1
(1)
n1
n
2
=

2
12
,

n=1
(1)
n1
(2n 1)
3
=

3
32
3.4 Convergencia de la serie de Fourier
Denicin 3.7 (Funcin continua a pedazos) Sea f denida en [a, b] excepto quizs en un
nmero nito de puntos. Se dice que f es continua a pedazos si:
1. f es continua en [a, b] excepto quizs en un nmero nito de puntos.
2. Los lmites laterales lim
xa
+ f (x) y lim
xb
f (x) existen y son nitos.
3. Si x
0
(a, b) es un punto de discontinuidad, entonces los lmites laterales en este punto existen
y son nitos.
Ejemplo 3.8 La siguiente funcin es continua a pedazos en [5, 2]
f (x) =
_
_
x
2
6x 8 x [5, 1]
2x
2
x (1, 1)
x [1, 2]
sin(x) (2, 4]
-5 -4 -3 -2 -1
0
1 2 3 4
-3
-2
-1
1
2
x
y
Denicin 3.8 (Funcin suave a pedazos) Una funcin f es suave a pedazos en [a, b] si f y f
son continuas a pedazos en [a, b] .

Ejemplo 3.9 Con referencia al ejemplo 3.8, su derivada es
f
(x) =
_
_
2x 6 x [5, 1)
4x x (1, 1)
1 (1, 2)
cos (x) (2, 4]
ntese que f
(x) es continua a pedazos en [5, 4] por tanto f es suave a pedazos en dicho intervalo.
Denicin 3.9 (Lmites por la izquierda y derecha) Los lmites por la izquierda y por la
derecha en un punto a se escribirn como:
f (a+) = lim
xa
+
f (x)
f (a) = lim
xa
f (x)
3.4. CONVERGENCIA DE LA SERIE DE FOURIER 59
Teorema 3.10 (Convergencia de la serie de Fourier)Sea f suave a pedazos en [L, L] , en-
tonces la serie de Fourier de f converge a
f (x+) +f (x)
2
para x (L, L) ,
en particular si f es continua en x, la serie converge a f (x) .
Ejemplo 3.10 Nuevamente nos referimos al ejemplo 3.8, a continuacin se muestra las grcas de
la funcin y su serie de Fourier terica.
-5 -4 -3 -2 -1
0
1 2 3 4
-3
-2
-1
1
2
x
y
-5 -4 -3 -2 -1
0
1 2 3 4
-3
-2
-1
1
2
x
y
2
1
2
1
Funcin f (x) Grfica de la serie de Fourier
debe notarse que la serie de Fourier converge a f (x) en (5, 1)(1, 1)(1, 2)(2, 4) y al promedio
de lmites laterales en los puntos de discontinuidad, ms concretamente a:
f (1+) +f (1)
2
=
2 + (3)
2
=
1
2
en x = 1
f (1+) +f (1)
2
=
1 + 2
2
=
1
2
en x = 1
f (2+) +f (2)
2
=
0 + (2)
2
= 1 en x = 2
Ejemplo 3.11 Considrese el ejemplo 3.4 pgina 50 donde f (x) = x, denida en [, ] . Se prueba
que su serie de Fourier es
n=1
2 (1)
n+1
n
sin(nx) ,
puesto que f es continua en (, ) podemos escribir
f (x) =

n=1
2 (1)
n+1
n
sin(nx) , para todo x (, ) .
3.4.1 Convergencia en los extremos
Si f est denida en [L, L] el teorema 3.10 no dice sobre la convergencia en (L, L) pero no
dice nada sobre la convergencia en L y L. En esta seccin discutiremos la convergencia en los
extremos. Debemos notar que aunque la funcin f est denida slo en [L, L] , su serie de Fourier
est denida en toda la recta real en donde la serie sea convergente. Para tener coherencia entre f y
su serie de Fourier, consideramos la extensin peridica de f a toda la recta real, vease la denicin
3.1 pgina 43. a continuacin se muestra la grca de una funcin f denida en [L, L] extendida
peridicamente en R.
Funcin extendida peridicamente
L 2 L 2 L L
y
x
Llamando f
P
a la extensin peridica y aplicando el teorema 3.10 debemos tener que la serie en L
converge a:
f
P
(L) +f
P
(L+)
2
=
f (L) +f (L+)
2
anlogamente en L se tiene:
f
P
(L) +f
P
(L+)
2
=
f (L) +f (L+)
2
por tanto la serie de Fourier converge en L y L al mismo punto.
3.4.2 El fenmeno de Gibbs
Nuevamente consideremos el ejemplo 3.4 pgina 50 donde f (x) = x, denida en [, ] y extendida
peridicamente. Se prueba que
f (x) =

n=1
2 (1)
n+1
n
sin(nx) ,
esta serie converge a x para todo x = , 2, . . . y converge a 0 para x = , 2, . . . .,
A continuacin se presentan algunos grcos que corresponden a algunos valores de M en
f (x, M) =
M
n=1
2 (1)
n+1
n
sin(nx)
3.5. DERIVACIN E INTEGRACIN DE LAS SERIES DE FOURIER 61
2 0 -2
2
1
-1
-2
2 0
-
2
2
1
-1
-2
2 0 -2
2
1
-1
-2
2 0 -2
2
1
0
-1
-2
2 0 -2
2
1
-1
-2
2 = M 4 = M
20 = M
10 = M
30 = M

Se puede apreciar que a medida que M crece la convergencia en los puntos de continuidad es
rpida, no as en los puntos de discontinuidad, ms an en estos puntos poco a poco se presenta
un pico en el salto hacia arriba y hacia abajo. La longitud de este salto es aproximadamente 18%
de la magnitud del salto de la discontinuidad (la diferencia de los lmites laterales). Para nuestro
ejemplo el salto es 2, por tanto la magnitud del salto hacia arriba y hacia abajo es aproximadamente
(0.18) (2) = 1. 13.
3.5 Derivacin e integracin de las series de Fourier
3.5.1 Integracin
Sea f (x) una funcin que que tiene una serie de Fourier, entonces el desarrollo de la serie de Fourier
de f (x) puede integrarse trmino a trmino y la serie integrada converge a la integral de f (x) .
Concrtamente si f es peridica de periodo P con desarrollo
f (x) =
1
2
a
0
+

n=1
_
a
n
cos
2nx
P
+b
n
sin
2nx
P
_
entonces para 0 x
1
< x x
_
x
x
1
f (x) dx =
1
2
a
0
_
x
x
1
dx +

n=1
_
a
n
_
x
x
1
cos
2nx
P
dx +b
n
_
x
x
1
sin
2nx
P
dx
_
=
1
2
a
0
(x x
1
) +

n=1
_
P a
n
2n
sin
2nx
P
x
x
1
P b
n
2n
cos
2nx
P
x
x
1
_
=
1
2
a
0
(x x
1
) +

n=1
_
P a
n
2n
_
sin
2nx
P
sin
2nx
1
P
_
P b
n
2n
_
cos
2nx
P
cos
2nx
1
P
__
de donde:
_
x
x
1
f (x) dx =
1
2
a
0
(x x
1
)+

n=1
_
P a
n
2n
_
sin
2nx
P
sin
2nx
1
P
_
P b
n
2n
_
cos
2nx
P
cos
2nx
1
P
__
claramente la parte izquierda de la anterior igualdad no es una serie de Fourier por la presencia del
trmino
1
2
a
0
x, sin embargo transponiendo trminos se puede observar que se tendr el desarrollo en
serie de Fourier de g (x) =
_
x
x
1
f (x) dx
1
2
a
0
x.
Ejemplo 3.12 Nuevamente consideremos el ejemplo 3.4 pgina 50donde f (x) = x, denida en
[, ] y extendida peridicamente. Se prueba que
x =

n=1
2 (1)
n+1
n
sin(nx) ,
entonces integrando de 0 a x se encuentra:
1
2
x
2
=

n=1
2 (1)
n+1
n
_
x
0
sin(nx) dx
=

n=1
2 (1)
n+1
n
_
1 cos nx
n
_
=

n=1
2 (1)
n+1
n
2

n=1
2 (1)
n+1
n
2
cos nx
=

n=1
2 (1)
n+1
n
2
+

n=1
2 (1)
n
n
2
cos nx
Para vericar este desarrollo calcularemos por separado la serie de Fourier de g (x) =
1
2
x
2
,
deninido en (, ) . Claramente esta funcin es par, por tanto en su desarrollo slo aparecen
trminos en cosenos.
a
0
=
4
2
_

0
1
2
x
2
dx =
1
3
2
a
n
=
4
2
_

0
_
1
2
x
2
cos (nx)
_
dx
=
2 (1)
n
n
2
por tanto:
1
2
x
2
=
1
3
2
+

n=1
2 (1)
n
n
2
cos nx
slo nos falta probar que
1
3
2
=

n=1
2 (1)
n+1
n
2
, para esto empleamos la anterior igualdad con
x = 0, en tal caso se tendr:
0 =
1
3
2
+

n=1
2 (1)
n
n
2
de donde:
1
3
2
=

n=1
2 (1)
n
n
2
=

n=1
2 (1)
n+1
n
2
con lo que termina la vericacin.
3.5. DERIVACIN E INTEGRACIN DE LAS SERIES DE FOURIER 63
3.5.2 Derivacin
Teorema 3.11 Sea f continua en [L, L] y supongamos que f (L) = f (L) . Sea f
(x) continua a
pedazos en [L, L] . Entonces f (x) es igual a su serie de Fourier para x [L, L] .,
f (x) =
1
2
a
0
+

n=1
_
a
n
cos
nx
L
+b
n
sin
nx
L
_
y en cada donde en (L, L) donde f
(x) existe,
f
(x) =

n=1
n
L
_
a
n
sin
nx
L
+b
n
cos
nx
L
_
Ejemplo 3.13 Sea f (x) =
_
1 x (0, 1)
1 x (1, 0)
, es una funcin impar, por tanto slo se tienen
trminos en seno.
b
n
=
2
2
__
0
1
sin(nx) dx
_
1
0
sin(nx) dx
_
= 2
1 + (1)
n
n
por tanto su serie de Fourier es:
f (x) =

n=1
2 (1 + (1)
n
)
n
sin(nx)
si derivamos trmino a trmino se encuentra:
f
(x) =

n=1
2 (1 + (1)
n
) cos (nx)
La anterior serie no es convergente
1
. Este resultado se explica por el hecho de que la funcin f
no es contnua.
Ejemplo 3.14 Consideremos ahora la funcin f (x) = 1 x
2
denida en (1, 1) . Esta funcin es
par por tanto slo se tienen trminos en coseno.
a
0
=
2
2
_
1
1
_
1 x
2
_
dx =
4
3
a
n
=
2
2
_
1
1
_
1 x
2
_
cos (nx) dx
= 4
(1)
n
2
n
2
1
Como se sabe si el n esimo trmino de una serie

n=1
an converge entonces lim
n
an = 0. De donde se deduce que
si lim
n
an = 0, entonces

n=1
an no es convergente.
por tanto la serie de Fourier es:
1 x
2
=
2
3
+

n=1
4
(1)
n
2
n
2
cos nx
derivando obtenemos
2x =

n=1
4
(1)
n
n
sinnx.
Ejercicio
Pruebe que la funcin peridica f (x) = x, x (T, T) extendida peridicamente tiene como serie
de Fourier
f (x) =
2T
_
sin
x
T

1
2
sin
2x
T
+
1
3
sin
3x
T

1
4
sin
4x
T
+
_
integrando trmino a trmino esta serie pruebe que g (x) = x
2
, x (T, T) extendida peridicamente
tiene serie de Fourier
g (x) =
1
3
T
2
4T
2
2
_
cos
x
T

1
2
2
cos
2x
T
+
1
3
2
cos
3x
T

1
4
2
cos
4x
T
+
_
3.6 La serie de Fourier compleja
Supngase que f es una funcin peridica con periodo P y
f (x) =
1
2
a
0
+

n=1
a
n
cos
2nx
P
+b
n
sin
2nx
P
tomando en cuenta que:
cos
2nx
P
=
1
2
_
e
i2mx/P
+e
i2mx/P
_
sin
2nx
P
=
i
2
_
e
i2mx/P
e
i2mx/P
_
se tiene:
f (x) =
1
2
a
0
+

n=1
a
n
1
2
_
e
i2mx/P
+e
i2mx/P
_
b
n
i
2
_
e
i2mx/P
e
i2mx/P
_
=
1
2
a
0
+

n=1
_
1
2
(a
n
ib
n
) e
i2mx/P
+
1
2
(a
n
+ib
n
) e
i2mx/P
_
ntese que
a
n
=
2
P
_
P
0
f (x) cos
2 (n) x
P
dx
=
2
P
_
P
0
f (x) cos
2nx
P
dx
= a
n
3.7. UNA APLICACIN 65
anlogamente, se puede probar que:
b
n
= b
n
denimos:
c
n
=
1
2
(a
n
ib
n
)
claramente:
c
n
=
1
2
(a
n
+ib
n
) y c
0
=
1
2
a
0
por tanto:
f (x) = c
0
+

n=1
_
c
n
e
i2mx/P
+c
n
e
i2mx/P
_
= c
0
+

n=
n=0
c
n
e
i2mx/P
=

n=
c
n
e
i2mx/P
Finalmente notemos que:
c
n
=
1
2
(a
n
ib
n
)
=
1
2
2
P
_
P
0
f (x)
_
cos
2nx
P
i sin
2nx
P
_
dx
=
1
P
_
P
0
f (x) e
i2nx/P
dx
La expansin
f (x) =

n=
c
n
e
i2nx/P
, c
n
=
1
P
_
P
0
f (x) e
i2nx/P
dx,
se llama serie de Fourier compleja.
3.7 Una aplicacin
En esta seccin se presenta una tcnica para calcular la solucin de una ecuacin diferencial a
derivadas parciales, concretamente resolveremos las ecuaciones del calor y la onda.
3.7.1 La ecuacin del calor
La siguiente ecuacin diferencial modela el ujo del calor sin fuentes en un alambre uniforme cuyos
extremos se mantienen a temperatura constante cero:
u(x, t)
t
=
2
u(x, t)
x
2
u(0, t) = u(L, t) = 0, t > 0
u(x, 0) = f (x) , 0 < x < L
donde u(x, t) es la temperatura del alambre en el punto x y en el tiempo t.
Sean X = X (x) , T = T (t) supngase que u(x, t) = X (x) T (t) , entonces:
u
t
= XT
,

2
u
x
2
= X
T
reemplazando estas derivadas en la ecuacin del calor se encuentra:
XT
= X
T
de donde
T
T
=
X
X
,
puesto que cada lado de esta ecuacin es funcin de una sla variable, se debe tener forzosamente
T
T
=
X
X
= k, con k una constante. Por tanto se tienen las ecuaciones diferenciales ordinarias:
T
kT = 0 y X
kX = 0,
de las condiciones de frontera se encuentra:
De u(0, t) = u(L, t) = 0 para t > 0, se encuentra X (0) T (t) = X (L) T (t) = 0 luego X(0) =
X (L) = 0.
As se tiene la ecuacin diferencial ordinaria
X
kX = 0, X (0) = X (L) = 0,
resolvamos esta ecuacin tomando en cuenta tres casos:
Caso k > 0. La ecuacin caracterstica es r
2
k = 0, es decir r =
k, por tanto la solucin

general es
X (x) = A
1
e
kt
+A
2
e
kt
,
para encontrar las constantes A
1
y A
2
aplicamos las condiciones de frontera, por tanto:
A
1
+A
2
= 0
A
1
e
L
k
+A
2
e
L
k
= 0
el determinante de la matriz de coeciente de este sistema homogneo es D = e
L
k
e
L
k
= 0
para todo k > 0, por tanto la nica solucin es: A
1
= A
2
= 0, es decir, no existe una solucin no
nula para k > 0.
Caso k = 0. La solucin en este caso es:
X (x) = A
1
+A
2
x,
aplicando las condiciones de frontera,
A
1
= 0
A
1
+A
2
L = 0
de donde A
1
= A
2
= 0. Nuevamente en este caso no se tienen soluciones no nulas.
3.7. UNA APLICACIN 67
Caso k < 0. En este caso la ecuacin caracterstica es r
2
k = 0, de donde r = i
k, por
tanto la solucin general es:
X (x) = A
1
cos
kx +A
2
sin
kx
aplicando condiciones de frontera:
A
1
= 0
A
1
cos
kL +A
2
sin
kL = 0
de donde: A
2
sin
_
kL
_
= 0, para tener soluciones no triviales elegimos

kL = n, para n N.
por tanto las soluciones no triviales de la ecuacin diferencial son:
X
n
= a
n
, n = 1, 2, . . .
Ahora que tenemos soluciones no triviales, buscamos T (t) . De

kL = n, se encuentra k =
n
2
2
L
2
, por tanto se tiene la ecuacin diferencial:
T
+
n
2
2
L
2
T = 0
de donde para n = 1, 2, . . . se tiene la solucin
T
n
= b
n
e
n
2
2
L
2
t
por tanto la solucin general de la ecuacion diferencial dada es
u(x, t) =

n=1
c
n
e
n
2
2
L
2
t
sin
_
nx
L
_
Finalmente aplicando la condicin u(x, 0) = f (x) , se encuentra
n=1
c
n
sin
_
nx
L
_
= f (x) , 0 < x < L.
esto muestra que las constantes de integracin c
n
se encuentran realizando el desarrollo en serie de
Fourier en senos de la funcin f (x) en el intervalo (0, L) .
3.7.2 La ecuacin de la onda
Considrese el problema de una cuerda estirada entre dos puntos. Se quiere determinar una funcin
u(x, t) que proporcione el desplazamiento de la cuerda en cualquier punto x [0, L] y cualquier
instante t 0. Este problema se modela con:
2
u(x, t)
2
t
=
2
2
u(x, t)
x
2
u(0, t) = u(L, t) = 0, t > 0
u(x, 0) = f (x) , 0 < x < L
u
t
(x, 0) = g (x) , 0 < x < L
(Resolver el problema)
Captulo 4
La transformada de Fourier
Las series de Fourier se emplean para representar funciones peridicas cuando se satisfacen ciertas
condiciones. Si la funcin no es peridica, entonces no puede representarse con una serie Fourier
para todo x R. Sin embargo cuando esto ocurre an podemos representar f en trminos de seno
y coseno, aunque en este caso la sumatoria se convertir en integral, la idea es simple, suponemos
que el periodo de la funcin es innito.
4.1 La integral de Fourier
Sea f una funcin no peridica tal que
_
|f (x)| dx < y es suave a pedazos en cada intervalo

[L, L] , entonces sabemos que en [L, L] f tiene serie de Fourier, esta es:
1
2L
_
L
L
f (y) dy +

n=1
__
1
L
_
L
L
f (y) cos
_
ny
L
_
dy
_
cos
nx
L
+
_
1
L
_
L
L
f (y) sin
_
ny
L
_
dy
_
sin
nx
L
_
haremos que L , para esto denimos:
w
n
=
n
L
y w
n
w
n1
=

L
= w
(claramente w 0 si L ), con esto, la anterior serie se escribe como:
1
2
__
L
L
f (y) dy
_
w +
1
n=1
___
L
L
f (y) cos (w
n
y) dy
_
cos (w
n
x)
+
__
L
L
f (y) sin(w
n
y) dy
_
sin(w
n
x)
_
w
tomando L , se tienen los siguientes resultados:
__
L
L
f (y) dy
_
w 0
n=1
__
L
L
f (y) cos (w
n
y) dy
_
cos (w
n
x) w
_

0
__

(f (y) cos (wy) dy)

_
cos (wx) dw
n=1
__
L
L
f (y) sin(w
n
y) dy
_
sin(w
n
x) w
_

0
__

(f (y) sin(wy) dy)

_
sin(wx) dw
69
70 CAPTULO 4. LA TRANSFORMADA DE FOURIER
por tanto la serie de Fourier, cuando L queda como
_

0
_
1
(f (y) cos (wy) dy) cos (wx) +

1
(f (y) sin(wy) dy) sin(wx)

_
dw
que puede escribirse como:
_

0
[A
w
cos (wx) +B
w
sin(wx)] dw
donde A
w
y B
w
son
A
w
=
1
f (y) cos (wy) dy

B
w
=
1
f (y) sin(wy) dy,

Denicin 4.1 (Integral de Fourier) Se dene como
_

0
[A
w
cos (wx) +B
w
sin(wx)] dw
donde A
w
y B
w
se llaman los coecientes de la integral de Fourier.
Por las hipotesis hechas sobre f, sabemos que:
f (x+) +f (x)
2
=
_

0
[A
w
cos (wx) +B
w
sin(wx)] dw.
Ejemplo 4.1 Sea a > 0, denimos
f (x) =
_
e
ax
x 0
0 x < 0
-2 -1 0 1 2 3
-1
1
2
-3
x
y
2 con ,
0 , 0
0 ,
) ( =
<
=

a
x
x e
x f
ax
Notemos que
_
f (x) dx =
_
0
e
ax
dx =
1
a
< .
A
w
=
1
f (y) cos (wy) dy

=
1
_

0
e
ay
cos (wy) dy
4.1. LA INTEGRAL DE FOURIER 71
=
1
a
a
2
+w
2
e
ay
cos wy +
w
a
2
+w
2
e
ay
sinwy
0
_
=
1
a
a
2
+w
2
B
w
=
1
f (y) sin(wy) dy
=
1
_

0
f (y) sin(wy) dy
=
1
w
a
2
+w
2
e
ay
cos wy
a
a
2
+w
2
e
ay
sinwy
0
_
=
1
w
a
2
+w
2
Por tanto la integral de Fourier para esta funcin es:
_

0
[A
w
cos (wx) +B
w
sin(wx)] dw =
1
_

0
_
acos (wx)
a
2
+w
2

wsin(wx)
a
2
+w
2
_
dw.
Puesto que el nico punto de discontinuidad es x = 0, se tiene:
1
_

0
_
a cos (wx)
a
2
+w
2

wsin(wx)
a
2
+w
2
_
dw =
_
_
_
0 x < 0
1/2 x = 0
e
ax
x > 0
Ejemplo 4.2 Considrese la siguiente funcin:
f (x) =
_
1 |x| 1
0 |x| > 1
claramente
_
|f (x)| < . Calculamos A

w
y B
w
.
A
w
=
1
f (y) cos (wy) dy

=
1
_
1
1
cos (wy) dy
=
2
sinw
w
B
w
=
1
f (y) sin(wy) dy
=
1
_
1
1
sin(wy) dy
= 0
Ntese que B
w
es cero, como se esperaba. Por tanto la integral de Fourier es:
_

0
[A
w
cos (wx) +B
w
sin(wx)] dw =
_

0
_
2
sinw
w
cos (wx)
_
dw
=
2
_

0
cos wx sinw
w
dw
De acuerdo al marco terico se debe tener:
2
_

0
cos wx sinw
w
dw =
_
_
_
1 |x| < 1
1/2 x = 1
0 |x| > 1
Ejercicios
Hallar la integral de Fourier correspondiente a las siguientes funciones:
1. f (x) = e
|x|
. Sol.
2
_

0
cos (wx)
(1 +w
2
)
dw
2. f (x) = xe
|x|
. Sol.
4
_

0
wsin(wx)
(1 +w
2
)
2
dw.
3. f (x) =
_
x, |x| 1
0, |x| > 1
. Sol.
2
_

0
_
sinw +wcos w
w
2
_
sin(wx) dw.
4. Utilizar la funcin f (x) = xe
x
, x [0, ) , para probar:
_

0
1 w
2
(1 +w
2
)
2
cos (wx) dw =
_

0
2w
(1 +w
2
)
2
sin(wx) dw
para x 0.
4.2 La integral de Fourier compleja y la transformada de Fourier
Si f es suave a pedazos en cada intevalo de la forma [L, L] entonces:
f (x+) +f (x)
2
=
_

0
_
1
(f (y) cos (wy) dy) cos (wx) +

1
(f (y) sin(wy) dy) sin(wx)

_
dw
=
_

0
_
1
f (y) [cos (wy) cos (wx) + sin(wy) sin(wx)] dy

_
dw
=
1
_

0
_

f (y) cos (w(y x)) dy dw

=
1
2
_

0
_

f (y)
_
e
iw(yx)
+e
iw(yx)
_
dy dw
mediante propiedades de integracin se puede probar que:
f (x+) +f (x)
2
=
1
2
_

f (y) e
iw(yx)
dy dw
esta es la representacin compleja de la integral de Fourier, con
C
w
=
_

f (y) e
iwy
dy
4.2. LA INTEGRAL DE FOURIER COMPLEJA Y LA TRANSFORMADA DE FOURIER 73
se tiene:
f (x+) +f (x)
2
=
1
2
_

C
w
e
iwx
dw
C
w
se llamar coeciente de la integral de Fourier compleja de f.
Denicin 4.2 (Transformada de Fourier) Dada una funcin f para el cual
_
|f (x)| dx <
, la transformada de Fourier de f es la funcin denida por
F [f] (w) =
_

f (x) e
iwx
dx.
Por comodidad en lugar de escribir F [f] (w) en ocasiones escribiremos simplemente

f (w) .
Denicin 4.3 (Transformada inversa de Fourier) Se dene por
f (x) =
1
2
_

f (w) e
iwx
dw,
a veces escribiremos F
1
_
f (w)
_
(x) = f (x) . La transformada y su inversa constituyen un par de
transformadas para la transformada de Fourier.
Ejemplo 4.3 Sea a > 0, y
f (x) =
_
e
ax
x 0
0 x < 0
La Transformada de Fourier es:
F [f (x)] (w) =
_

0
e
ax
e
iwx
dx
=
e
ax
e
iwx
a +iw
0
=
1
a +iw
La funcin de Heaviside
La funcin de Heaviside se dene por:
H (x) =
_
1 x 0
0 x < 0
para a R, una traslacin de H es H (x a) .
1 1
x
x
y y
a
( ) x H ( ) a x H
Funcin de Heaviside Funcin de Heaviside trasladada
Una propiedad de la funcin de Heaviside es: H (x) = 1 H (x) .
La funcin pulso
Para a > 0, la funcin pulso se dene por:
f (x) =
_
k a x < a
0 x < a, x a
k
x
y
a
( ) ( ) ( ) a x H a x H k +
a
La transformada de la funcin pulso para w = 0 es:
F [k (H (x +a) H (x a))] (w) =
_

k (H (x +a) H (x a)) e
iwx
dx
= k
_
a
a
e
iwx
dx
=
2k sin(aw)
w
Si w = 0,
f (0) = k
_
a
a
dx = 2ka
luego:
F [k (H (x +a) H (x a))] (w) =
_
_
_
2k sin(aw)
w
w = 0
2ka w = 0
Todas las funciones denidas de a pedazos pueden escribirse en trminos de la funcin de Hea-
viside.
Ejemplo 4.4 Sea a > 0, y
f (x) =
_
e
ax
x 0
0 x < 0
Puede escribirse como f (x) = H (t) e
ax
, recordemos que
F
_
H (t) e
ax
(w) =
1
a +iw
.
Ejemplo 4.5 Sea
f (x) =
_
_
_
0 x < a
1 a x < b
0 b x
4.3. PROPIEDADES DE LA TRANSFORMADA DE FOURIER 75
entonces:
f (x) = 0 +H (x a) 1 +H (x b) (0 1)
= H (x a) H (x b)
Ejemplo 4.6 Sea
f (x) =
_
_
0 x < 2
x
2
2 x < 1
2x 1 x < 2
0 2 x
entonces:
f (x) = 0 +H (x + 2) x
2
+H (x 1)
_
2x x
2
_
+H (x 2) (0 2x)
= H (x + 2) x
2
+H (x 1)
_
2x x
2
_
H (x 2) (2x)
Observacin. La anterior funcin pudo tambin escribirse como:
f (x) = (H (x + 2) H (x 1)) x
2
+ (H (x 1) H (x 2)) 2x
4.3 Propiedades de la transformada de Fourier
Linealidad
Si y son complejos, entonces:
F [f (x) +g (x)] (w) = F [f (x)] (w) +F [g (x)] (w)
Corrimiento en x
Si x
0
es un nmero real:
F [f (x x
0
)] (w) =
_

f (x x
0
) e
iwx
dx
En esta ltima integral hagamos el cambio u = x x
0
. Con este cambio:
F [f (x x
0
)] (w) =
_

f (u) e
iw(u+x
0
)
du
= e
iwx
0
_

f (u) e
iwu
du
= e
iwx
0
F [f (x)] (w)
= e
iwx
0
f (w)
por tanto:
F [f (x x
0
)] (w) = e
iwx
0
f (w)
La versin inversa del teorema de corrimiento es:
f (x x
0
) = F
1
_
e
iwx
0
f (w)
_
(x)
Corrimiento en frecuencia
Si w
0
es cualquier nmero real:
F
_
e
iw
0
x
f (x)
(w) =
_

e
iw
0
x
f (x) e
iwx
dx
=
_

f (x) e
i(ww
0
)x
dx
= F [f (x)] (w w
0
) .
Ntese que si

f (w) = F [f (x)] (w) , entonces
F
_
e
iw
0
x
f (x)
(w) =

f (w w
0
) .
La versin inversa es
e
iw
0
x
f (x) = F
1
_
f (w w
0
)
_
(x) .
Escalado
Si a es un nmero real no nulo, entonces:
F [f (ax)] (w) =
_

f (ax) e
iwx
dx
con el cambio u = ax, se encuentra:
dx =
1
a
du
1. Si a > 0, entonces se encuentra:
F [f (ax)] (w) =
1
a
_

f (u) e
i(w/a)u
du
=
1
a
f
_
w
a
_
2. Si a < 0, entonces se encuentra:
F [f (ax)] (w) =
1
a
_

f (u) e
i(w/a)u
du
=
1
a
_

f (u) e
i(w/a)u
du
=
1
a
f
_
w
a
_
por tanto
F [f (ax)] (w) =
1
|a|

f
_
w
a
_
La versin inversa es
|a| f (ax) = F
1
_
f
_
w
a
__
(x) .
4.3. PROPIEDADES DE LA TRANSFORMADA DE FOURIER 77
Inversin en x
F [f (x)] (w) =
_

f (x) e
iwx
dx
=
_

f (u) e
i(w)u
du
=
_

f (u) e
i(w)u
du
=

f (w)
Simetra
F
_
f (x)
_
(w) =
_

f (x) e
iwx
dx
=
_

__

f (y) e
iyx
dy
_
e
iwx
dx
= 2f (w)
Ntese que la integral de Fourier se deni como:
f (x) =
1
2
_

__

f (y) e
iwy
dy
_
e
iwx
dw
Tabla de transformadas
f (x)

f (w) parmetro
e
|x|
2
1 +w
2
F [(H (x +a) H (x a))] (w) =
_
_
_
2 sin(aw)
w
w = 0
2a w = 0
a R
1
a
2
+x
2

a
e
a|w|
a > 0
e
ax
2
_
a
e
w
2
/4a
a > 0
e
iax
f (x)

f (w a) a R
f (x a) e
iaw
f (w) a R
f (ax +b)
1
|a|
e
ibw
a

f
_
w
a
_
a = 0, b R
x
n
f (x) i
n
f
(n)
(w) n N
f (x) sin(ax)

f (w a)

f (w +a)
2i
a R
f (x) cos (ax)

f (w a) +

f (w +a)
2
a R
e
ax
H (x)
1
a +iw
Re (a) > 0
xe
ax
H (x)
1
(a +iw)
2
Re (a) > 0
x
n1
(n 1)!
e
ax
H (x)
1
(a +iw)
n
Re (a) > 0
Ejercicios
Hallar la transformada de Fourier de:
1. f (x) =
_
_
_
1, x [0, 1]
1, x [1, 0)
0, x > 1
. Sol.
2i
w
(cos w 1)
2. f (x) = 5 [H (x 3) H (x 1)] . Sol.
10
w
e
2iw
sinw
3. f (x) = 5e
3(x5)
2
. Sol. 5
_
3
e
(5iww
2
/12)
4. f (x) = H (x k) e
x/4
. Sol.
4
1+4iw
e
(1+4iw)k/4
5. f (x) = H (x k) x
2
. Sol. La solucin no est en trminos de funciones elementales.
6. f (x) = 2H (x 2) e
3x
. Sol.
2e
2iw6
3+iw
7. f (x) = H (2 x)
_
e
3x
+e
x
_
. Sol.
e
2iw+6
3iw
+
e
2iw+2
1iw
8. f (x) = 3e
4|x+2|
. Sol.
24
16+w
2
e
2iw
9. f (x) = H (x 3) e
2x
10. f (x) = 3e
4|x|
cos (2x) . Sol.
12
16+(w2)
2
+
12
16+(w+2)
2
11. f (x) =
sinx
4 +x
2
Sol.
i
4
_
e
2|w+1|
e
2|w1|
_
12. f (x) = H (x 1) e
5(x+2)
. Sol.
1
5 +iw
e
15iw
Hallar la transformada inversa de:
13.

f (w) = 9e
(w+4)
2
/32
. Sol. 18
_
2
e
8x
2
e
4ix
14.

f (w) =
e
(2w6)i
5 (3 w) i
. Sol. H (x + 2) e
10(53i)x
15.

f (w) =
1 +iw
6 w
2
+ 5iw
. Sol. H (x)
_
2e
3x
e
2x
_
4.4 Convolucin
Denicin 4.4 Sean f, g funciones denidas en Rtales que
_
b
a
f (x) dx y
_
b
a
f (x) dx existen en todo
intervalo [a, b] . Supngase que
_
|f (u) g (x u)| du < . En estas condiciones la convolucin de

f y g se dene por:
(f g) (x) =
_

f (u) g (x u) du
Es fcil probar el siguiente resultado:
4.4. CONVOLUCIN 79
Teorema 4.5 Supongamos que f g y f g existen entonces:
1. f g = g f
2. f (g +h) = f g +f h
Ejemplo 4.7 Sea f (x) = H (x) e
2x
, g (x) = H (x) e
5x
, entonces:
(f g) (x) =
_

f (u) g (x u) du
=
_

H (u) e
2u
H (x u) e
5(xu)
du
= e
5x
_

0
H (x u) e
3u
du
para evaluar esta integral consideramos los siguientes casos:
y
y
( ) 0 con < x u x H
( ) 0 con > x u x H
1
x u
1
x
u
0 0
(a) x < 0, en este caso
_

0
H (x u) e
3u
du = e
5x
_

0
0 e
3u
du = 0
(b) x > 0, en este caso
_

0
H (x u) e
3u
du = e
5x
_
x
0
1 e
3u
du
= e
5x
1
3
_
e
3x
1
_
=
1
3
_
e
2x
e
5x
_
por tanto
(f g) (x) = H (x)
1
3
_
e
2x
e
5x
_
.
Ejemplo 4.8 Sea f (x) = H (x + 2) H (x 2) , g (x) = H (x) e
5x
, entonces:
(f g) (x) =
_

f (u) g (x u) du
=
_

(H (u + 2) H (u 2)) H (x u) e
5(xu)
du
= e
5x
_
2
2
H (x u) e
5u
du
para evaluar esta integral consideramos los siguientes casos:
( ) 2 con < x u x H ( ) 2 con > x u x H
y
1
x
u
0 2 2
y
1
x u
0 2 2
y
1
x u
0 2 2
( ) 2 2 - con < < x u x H
(a) x < 2
(f g) (x) = e
5x
_
2
2
H (x u) e
5u
du
= e
5x
_
2
2
0 e
5u
du = 0
(b) 2 < x < 2
(f g) (x) = e
5x
_
2
2
H (x u) e
5u
du
= e
5x
_
x
2
1 e
5u
du
=
1
5
_
1 e
5(x+2)
_
(c) x > 2
(f g) (x) = e
5x
_
2
2
H (x u) e
5u
du
= e
5x
_
2
2
1 e
5u
du
=
1
5
_
e
5(x2)
e
5(x+2)
_
Por tanto
(f g) (x) = 0 +H (x + 2)
1
5
_
1 e
5(x+2)
_
+H (x 2)
_
1
5
_
e
5(x2)
e
5(x+2)
_
1
5
_
1 e
5(x+2)
_
_
=
1
5
H (x + 2)
_
1 e
5(x+2)
_
1
5
H (x 2)
_
1 e
5(x2)
_
Teorema 4.6 Supngase que f y g son continuas en R y que
_
|f (x)| dx < ,
_
|g (x)| dx <
. Entonces
1.
_

(f g) (x) dx =
__

f (x) dx
___

g (x) dx
_
4.4. CONVOLUCIN 81
2. Convolucin en el tiempo
F [(f g) (x)] (w) = F [f (x)] (w) F [g (x)] (w)
3. Convolucin en la frecuencia
F [f (x) g (x)] (w) =
1
2
F [f (x)] (w) F [g (x)] (w)
Demostracin.
1.
_

(f g) (x) dx =
_

__

f (u) g (x u) du
_
dx
=
_

__

f (u) g (x u) du
_
dx
=
_

__

f (u) g (x u) dx
_
du
=
_

_
f (u)
_

g (x u) dx
_
du
=
_

_
f (u)
_

g (x) dx
_
du
=
__

f (u) du
_ __

g (x) dx
_
=
__

f (x) dx
___

g (x) dx
_
2.
F [(f g) (x)] (w) =
_

(f g) (x) e
iwx
dx
=
_

__

f (u) g (x u) du
_
e
iwx
dx
=
_

__

_
f (u) e
iwu
_
_
g (x u) e
iw(xu)
du
_
_
dx
=
_

_
f (x) e
iwx
g (x) e
iwx
_
dx
=
__

f (x) e
iwx
dx
___

_
g (x) e
iwx
_
dx
_
= F [f (x)] (w) F [g (x)] (w)
3. De la denicin 4.3 (Pgina 73) se tiene
f (x) =
1
2
_

f (w) e
iwx
dw
entonces:
F [f (x) g (x)] (w) =
_

f (x) g (x) e
iwx
dx
=
1
2
_

__

f (y) e
iyx
dy
_
g (x) e
iwx
dx
=
1
2
_

__

f (y) g (x) e
ix(wy)
dy
_
dx
=
1
2
_

__

f (y) g (x) e
ix(wy)
dx
_
dy
=
1
2
_

f (y)
_

g (x) e
ix(wy)
dx
_
dy
=
1
2
_

f (y) g (w y)
_
dy
=
1
2
_

f (x) g (w x)
_
dx
=
1
2
F [f (x)] (w) F [g (x)] (w)
Ejemplo 4.9 Determinaremos la transformada inversa de
2 sin2w
w(5 +iw)
En primer lugar ntese que
2 sin2w
w(5 +iw)
=
2 sin2w
w
1
(5 +iw)
y
F
1
_
2 sin2w
w
_
(x) = H (x + 2) H (x 2)
F
1
_
1
5 +iw
_
(x) = H (t) e
5x
,
por tanto aplicando el anterior teorema:
F
1
_
2 sin2w
w
1
(5 +iw)
_
(t) = (H (x + 2) H (x 2))
_
H (t) e
5x
_
,
en el ejemplo 4.8 (pgina 79) se prueba que:
(H (x + 2) H (x 2))
_
H (t) e
5x
_
=
1
5
H (x + 2)
_
1 e
5(x+2)
_
1
5
H (x 2)
_
1 e
5(x2)
_
por tanto:
F
1
_
2 sin2w
w
1
(5 +iw)
_
(t) =
1
5
H (x + 2)
_
1 e
5(x+2)
_
1
5
H (x 2)
_
1 e
5(x2)
_
4.4. CONVOLUCIN 83
Ejercicios
Mediante convolucin determinar la transformada inversa de Fourier de:
1.
1
(4 +iw)
2
, Sol. xe
4x
H (x)
2.
1
(2 +iw) (3 iw)
, Sol.
1
5
_
e
3t
H (t) +e
2t
H (t)
_
3.
1
(2 +iw) (3 +iw)
, Sol. H (t)
_
e
2t
e
3t
_
4.
sin(4w)
w(3 +iw)
, Sol,
1
6
_
e
3(t4)
1
_
H (t 4) +
1
6
_
e
3(t+4)
+ 1
_
H (t + 4)
5.
1
(1 +w
2
) (4 +w
2
)
, Sol.
1
6
e
|x|
1
12
e
2|x|
Captulo 5
Operaciones diferenciales
5.1 El operador Nabla
El operador nabla se dene por:
=

x
i +

y
j +

z
k
este operador tiene las mismas propiedades que los vectores.
5.2 Funciones escalares y funciones vectoriales
Una funcin de la forma : D
f
R
3
R se llama funcin escalar y una funcin

A : D
A
R
3
R
3
se llamar funcin vectorial.
Ejemplo 5.1 (x, y, z) = x
2
y
3
+y cos z es una funcin escalar y

A(x, y, z) = xy
i +y cos z
j +x
2
y
k
es una funcin vectorial.
5.3 Gradiente
Sea = (x, y, z)una funcin escalar, el gradiente de ,escrito o grad () est denida por
=

x
i +

y
j +

z
k
Propiedades: El gradiente Tiene entre otras las siguientes propiedades:
1. Es ortogonal a las supercies (x, y, x) = C.
2. Apunta en la direccin en que la derivada direccional es mxima.
3. Su mdulo es igual a esta derivada direccional mxima.
4. Se anula en los puntos estacionarios (mximos, mnimos y puntos de silla)
Aplicaciones en fsica
El Gradiente se aplica en electromagnetismo y mecnica de uidos. En particular, existen muchos
campos vectoriales que puede escribirse como el gradiente de una funcin escalar. Uno de ellos es el
campo electrosttico, que deriva del potencial elctrico cuya ecuacin es

E = .
85
86 CAPTULO 5. OPERACIONES DIFERENCIALES
Todo campo que pueda escribirse como el gradiente de un campo escalar, se denomina potencial,
conservativo o irrotacional.
Teorema 5.1 Si y son funciones escalares, entonces:
( +) = +
Ejercicio 5.1 Calcular y || en el punto (x, y, z) = x
3
z
2
+ cos (yz) en el punto (2, 1, 1) .
Solucin. (x, y, z) = 3x
2
z
2
i z sin(yz)

j y sin(yz)

k, luego (2, 1, 1) = 12
i +
j +

k
Ejercicio 5.2 Sea r = x
i +y
j +z
k, hallar el gradiente de
r.
Solucin.

r =
_
x
2
+y
2
+z
2
_
1/4
, entonces
r
x
=
1
4
_
x
2
+y
2
+z
2
_
3/4
2x
r
y
=
1
4
_
x
2
+y
2
+z
2
_
3/4
2y
r
z
=
1
4
_
x
2
+y
2
+z
2
_
3/4
2z
de donde deducimos:
r =
1
2
_
x
2
+y
2
+z
2
_
3/4
_
x
i +y
j +z
k
_
=
1
2
r
3/2
r
Ejercicios
1. (a) Sea f una funcin a una variable, sea r = |r| , probar que f (r) =
f
(r)
r
r. (b) Empleando
el resultado (a) calcular sin
_
r
3
r
1
_
. Sol. (b) cos
_
r
3
r
1
_ _
3r +r
3
_
r.
2. Hallar (r) de modo que =
r
r
5
. Sol. =
1
3
r
3
+C.
3. (a) Probar que es un vector perpendicular a la supercie (x, y, z) = 0. (b) Determinar el
vector normal unitario a la supercie x
3
y +xyz = 0 en el punto (1, 1, 1) de la supercie. Sol.
(b) u =

i +

k
2
.
5.4. DIVERGENCIA 87
5.4 Divergencia
La divergencia de un campo vectorial mide la diferencia entre el ujo entrante y el ujo saliente de
un campo vectorial sobre la supercie que rodea a un volumen de control, por tanto, si la divergencia
en un punto es positiva, se dice que el campo posee manantiales, si la divergencia es negativa, se
dice que tiene sumideros.
Denicin 5.2 (Divergencia)Sea

A = A
1
i + A
2
j + A
3
k una funcin vectorial, la divergencia,

escrito

A o div
_
A
_
est denida por:

A =
A
1
x
+
A
2
y
+
A
3
z
Teorema 5.3 Si A y B son funciones vectoriales y una funcin escalar, entonces
1.
_
A+

B
_
=

A+

B
2.
_
A
_
= ()

A+
_

A
_
3. () =
2
=

2
x
2
+

2
y
2
+

2
z
2
, siendo
2
=

2
x
2
+

2
y
2
+

2
z
2
Denicin 5.4 (Solenoidal)Un campo vectorial

A tal que

A = 0 recibe el nombre de solenoi-
dal.
Ejercicio 5.3 Si n un entero, calcular
_
r
r
n
_
.
Solucin.
_
r
r
n
_
= (r
n
r)
= r
n
r +r
n
r
=
nr
n1
r
r r +r
n
(3)
= nr
n
+ 3r
n
= (n + 3) r
n
ntese que
_
r
r
3
_
= 0.
Ejercicios
1. Demostrar los teoremas de esta seccin.
2. Hallar
_
r
_
r
r
n
__
siendo n un entero.
3. Demostrar
2
f (r) =
d
2
f
dr
2
+
2
r
df
dr
4. Pruebe que los siguientes campos de vectores son solenoidales:
A = (2x + 9y)
i + (3y 4z)
j + (2x 5z)
B =
_
5x
2
yz +z
_
i +
_
3xy
2
z
_
j + 2xz
2
y
k
5.5 Rotacional
El rotacional es un operador vectorial que muestra la tendencia de un campo vectorial a rotar
alrededor de un punto.
Denicin 5.5 (Rotacional) Sea

A = A
1
i+A
2
j+A
3
k una funcin vectorial, la divergencia, escrito

A o rot (A) est denida por:
rot
_
A
_
=

A =
i

j

k
x

y

z
A
1
A
2
A
3
Denicin 5.6 (Irrotacional) Un campo

A es irrotacional si rot
_
A
_
=
0
Teorema 5.7 Si A y B son funciones vectoriales y una funcin escalar, entonces
1. (A+B) = A+B
2. (A) = () A+(A)
3. (AB) = B (A) A (B)
4. (AB) = (B ) AB( A) (A ) B +A( B)
5. (A B) = (B ) A+ (A ) B +B (A) +A(B)
6. () = 0
7. (A) = 0
8. (A) = ( A)
2
A
5.5. ROTACIONAL 89
Ejercicios
1. Probar los teoremas de esta seccin.
2. Hallar rot(r f (r) siendo f una funcin derivable.
3. Demostrar
_

A
_
=
2
A+
_

A
_
4. Demostrar que

A es irrotacional y determinar tal que =

A para los siguientes campos
de vectores:
(a)

A =
_
2xy +z
3
_
i +
_
x
2
+
_
cos yz
2
_
z
2
_
j +
_
2
_
cos yz
2
_
yz + 3xz
2
_
k
(b)

A =
_
y
2
z +yz
2
(x +y +z)
2
_
i +
_
x
2
z +xz
2
(x +y +z)
2
_
j +
_
x
2
y +xy
2
(x +y +z)
2
_
k
(c)

A =
_
y
2
z
3
+ 3x
2
y
2
z
_
i +
_
2xyz
3
+ 2x
3
yz
_
j +
_
3xy
2
z
2
+x
3
y
2
_
k
(d)

A = (e
yz
+ 1)
i + (xze
yz
+ 2y)
j +
_
xye
yz
+ 3z
2
_
k
5. Hallar
_
r
r
n
_
donde n es un entero. Sol.

0
6. Sea = (x, y, z) una funcin escalar. Calcular rot() . Sol.

0
7. Hallar (f (r) r) . Sol.

0
Captulo 6
La integral de supercie
6.1 La denicin de integral de supercie
Sea S una supercie, dividamos la supercie en M pedazos de supercie S
i
, i = 1, 2, . . . , M, en
cada pedazo de supercie tomemos un punto P
i
de coordenadas (x
i
, y
i
, z
i
) . Sea

A
i
=

A(x
i
, y
i
, z
i
) y
n
i
el vector normal unitario exterior a S
p
en P. Formemos la suma:
M
i=1
A
i
n
i
S
i
,
el lmite de esta suma cuando M tal que el rea del mayor elemento S
i
tienda a cero, si
existe, se llama integral de supercie y se denota por:
__
S
A ndS, es decir:
__
S
A n dS = lim
M
M
i=1
A
i
n
i
S
i
donde n el es vector normal unitario a S en cualquier punto.
x
y
z
i
P
i
S
i n
La integral de supercie de un campo vectorial

A sobre una supercie S recibe tambin el nombre
de ujo de

A a travs de S por extensin del caso fsico del campo de velocidades de un uido.
91
92 CAPTULO 6. LA INTEGRAL DE SUPERFICIE
6.2 Clculo de la integral de supercie
Teorema 6.1 Sea R la proyeccin de la supercie sobre el plano xy, entonces
__
S
A ndS =
_ _
R
A n
dxdy
x
y
i i
y x
z
R
i
S
i
n
r
S
i
P
Si la proyeccin es sobre xz :
__
S
A ndS =
_ _
R
A n
dxdz
Si la proyeccin es sobre yz :
__
S
A ndS =
_ _
R
A n
dy dz
Ejercicio 6.1 Hallar
__
S
A ndS Si

A = y
i + 2x
j z
k y S la supercie del plano 2x + y = 6

situada en el primer octante y limitada por el plano z = 4.
Solucin. A continuacin se muestra la supercie S y la regin R que es proyeccin de S sobre
el plano xz.
x
y
z
6
3
4
4 = z
6 2 = + y x
R
6.2. CLCULO DE LA INTEGRAL DE SUPERFICIE 93
El vector normal unitario n es
n =
2
i +

j + 0
5
Proyectando S sobre el plano xz se encuentra el rectngulo {(x, z) : 0 x 3, 0 z 4} , adems:
=
1
A n =
_
y
i + 2x
j z
k
_
_
2
i +

j + 0
5
_
=
2y + 2x
5
=
2 (6 2x) + 2x
5
=
12 2x
5
por tanto:
__
S
A ndS =
_
3
0
_
4
0
12 2x
5
1
5
dxdz
=
_
4
0
_
3
0
(12 2x) dxdz
=
_
4
0
(27) dz
= 108
Ejercicio 6.2 Hallar
__
S
A ndS donde

A = z
i +y
j +2z
k, y S es parte del paraboloide x

2
+y
2
=
1 z para el cual z 0.
Solucin.
x
y
z
R
1
1
1
1
S
n
r
Sea = x
2
+y
2
+z 1, entonces:
n =

||
=
2x
i + 2y
j +

k
_
4x
2
+ 4y
2
+ 1
A n =
2xz + 2y
2
+ 2z
_
4x
2
+ 4y
2
+ 1
=
1
_
4x
2
+ 4y
2
+ 1
de donde
A n
= 2xz + 2y
2
+ 2z
= 2x
_
1 x
2
y
2
_
+ 2y
2
+ 2
_
1 x
2
y
2
_
Por tanto:
_ _
S
A ndS =
_ _
R
_
2x
_
1 x
2
y
2
_
+ 2y
2
+ 2
_
1 x
2
y
2
__
dxdy
realizemos el cambio de variables a coordenadas polares, es decir:
x = r cos
y = r sin
con lo que
__
S
A ndS =
_
2
0
__
1
0
_
2 (r cos )
_
1 r
2
_
+ 2
_
r
2
sin
2
_
+ 2
_
1 r
2
__
r dr
_
d
=
_
2
0
_
1
0
_
2 (cos )
_
r
2
+r
4
_
2r
3
_
cos
2
_
+ 2r
_
dr d
=
_
2
0
_
4
15
cos + 1
1
2
cos
2
_
d
=
3
2
Ejercicios
1. Hallar
__
S
A ndS donde

A = x
i + y
j + 2z
k y S es la parte del paraboloide de ecuacin

x
2
+y
2
= 1 z con z 0. Sol. 2.
2. Hallar
__
S
AndS donde

A = 4xz
i+xyz
2
j +3z
k y S es la supercie que encierra el volumen

dado por parte de la supercie z
2
= x
2
+y
2
el plano z = 0 y el plano z = 4. Sol. 320.
6.3. TEOREMA DE LA DIVERGENCIA DE GAUSS 95
3. Hallar
__
S
A ndS donde

A = 18z
i 12
j + 3y
k y S la regin del plano 2x + 3y + 6z = 12

en el primer octante. Sol. 24.
4. Sea

F = y
i + (x 2xz)

j xy
k, Hallar
__
S
_

F
_
n dS donde S es la supercie x
2
+
y
2
+z
2
= 9 por encima del plano xy. Sol. 0.
5. Hallar
__
S
A ndS donde

A = 6z
i + (2x +y)

j x
k y S es la supercie del volmen del

primer octante limitado por x
2
+z
2
= 9, x = 0, y = 0, z = 0, y = 8. Sol. 18.
6. Hallar
__
S
F ndS, donde

F = 2y
i z
j +x
2
k y S la supercie y
2
= 8x situada en el primer
octante y limitada por los planos y = 4, z = 6. Sol. 132.
6.3 Teorema de la divergencia de Gauss
Teorema 6.2 (Teorema de la divergencia de Gauss) Sea V el volumen limitado por una supercie
cerrada S y

A una funcin vectorial con derivadas parciales continuas, entonces:
__
S
A ndS =
_ _ _
V
_

A
_
dV
Ejercicio 6.3 Comprobar el teorema de la divergencia de Gauss para
__
S
AndS, donde

A = 2x
2
y
i y
2
j + 4xz
2
k y S la supercie cerrada del primer octante limitada por y

2
+z
2
= 9 y x = 2.
Solucin.
x
y
z
0 :
1
= z S
2 2 2
5
3 : = +z y S
2 :
4
= x S
0 :
2
= y S
0 :
3
= x S
2
3
3
(a) Empleando el teorema de divergencia.

A = 4xy 2y + 8xz
por tanto:
__
S
A ndS =
_ _ _
V
_

A
_
dV
=
_
2
0
_
3
0
_

9y
2
0
(4xy 2y + 8xz) dz dy dx
=
_
2
0
_
3
0
_
4xy
_
9 y
2
2y
_
9 y
2
4xy
2
+ 36x
_
dy dx
=
_
2
0
(108x 18) dx
= 180
(b) Sin emplear el teorema de divergencia.
(i) Sobre S
1
: Aqu la ecuacin de la supercie es z = 0, luego:
n =
k,
A n = 4xz
2
= 0,
= 1,
por tanto:
__
S
1
A ndS =
_ _
R
0 dxdy = 0
(ii) Sobre S
2
: Aqu la ecuacin de la supercie es y = 0, luego
n =
j,
A n = y
2
= 0,
= 1,
por tanto:
__
S
2
A ndS =
_ _
R
0 dxdz = 0
(iii) Sobre S
3
: Aqu la ecuacin de la supercie es x = 0, luego
n =
i,
A n = 2x
2
y = 0,
= 1,
por tanto:
__
S
3
A ndS =
_ _
R
0 dy dz = 0
(iv) Sobre S
4
: Aqu la ecuacin de la supercie es x = 2, luego
n =

i,
A n = 2x
2
y = 8y,
= 1,
por tanto:
__
S
3
A ndS =
_
3
0
_
_

9z
2
0
8y dy
_
dz
=
_
3
0
_
36 4z
2
_
dz
= 72
6.3. TEOREMA DE LA DIVERGENCIA DE GAUSS 97
(v) Sobre S
5
: Aqu la ecuacin de la supercie es y
2
+z
2
= 9, luego
n =
2y
j + 2z
k
_
4y
2
+ 4z
2
=
y
j +z
k
3
,
A n =
y
3
+ 4xz
3
3
=
z
3
,
por tanto:
__
S
3
A ndS =
_ _
R
y
3
+ 4xz
3
z
dxdy
siendo R el rectngulo {(x, y) : 0 x 2, 0 y 3} . Puesto que z =
_
9 y
2
se tiene:
__
S
3
A ndS =
_ _
R
y
3
+ 4xz
3
z
dxdy
=
_
3
0
_
2
0
y
3
+ 4x
_
9 y
2
_
3/2
(9 y
2
)
1/2
dxdy
=
_
3
0
_
2
y
3
36
_
(9 y
2
) + 4
_
(9 y
2
)y
2
_
(9 y
2
)
_
dy
= 108
Por tanto:
__
S
A ndS =
5
m=1
__
Sm
A ndS
= 0 + 0 + 0 + 72 + 108
= 180
Ejercicios
1. Hallar
__
S
A ndS, donde

A = x
3
i +x
2
y
j +x
2
z
k y S es la supercie cerrada que consiste

en el cilindro x
2
+y
2
= a
2
, z = 0 y z = b. Sol.
5
4
a
4
b
2. Hallar
__
S
F ndS, donde

F = 6z
i + (2x +y)
j x
k y S la supercie del volumen limitado

por el cilindro x
2
+z
2
= 9, x = 0, y = 0, z = 0, y = 8. Sol. 18.
3. Comprobar el teorema de divergencia de Gauss para

A = 4x
i 2y
2
j + z
2
k extendida a la
regin limitada por x
2
+y
2
= a
2
, z = 0 y z = b, donde a y b son positivos. Sol. b (4 +b) a
2
.
4. Comprobar el teorema de divergencia de Gauss para

A = 2x
2
y
i y
2
j 4xz
2
k extendida a la
regin del primer octante limitada por y
2
+z
2
= 9 y x = 2. Sol. 108.
Captulo 7
Coordenadas curvilneas
7.1 La denicin de coordenadas curvilneas
Considrense las coordenadas rectangulares x, y, z. Suponga que se hace la siguiente transformacin:
x = x(u
1
, u
2
, u
3
) , y = y (u
1
, u
2
, u
3
) , z = z (u
1
, u
2
, u
3
)
o despejando:
u
1
= u
1
(x, y, z) , u
2
= u
2
(x, y, z) , u
3
= u
3
(x, y, z)
donde se hace la suposicin de que todas las funciones son uniformes y con derivadas continuas.
Las nuevas coordenadas (u
1
, u
2
, u
3
) se llamarn coordenadas curvilneas.
Ejemplo 7.1 (Coordenadas esfricas)Son las ternas (r, , ) . Se relacionan con las coordenadas
cartesianas (x, y, z) mediante las ecuaciones:
x = r sin cos
y = r sin sin
z = r cos
para deducir estas ecuaciones se considera el siguiente grco:
r
x
y
z
( )
( ) z y x
r
, ,
, ,
sin r
cos r
cos r
sin r
O
P
A
B
C
Q
99
100 CAPTULO 7. COORDENADAS CURVILNEAS
CP = OQ = r sin
z = OC = r cos
x = OQ cos = r sin cos
y = OQ sin = r sin sin
Ntese que x
2
+y
2
+z
2
= r
2
.
7.2 Supercies y lneas de coordenadas
Sean c
1
, c
2
, c
3
constantes. Las supercies de ecuaciones:
u
1
= c
1
u
2
= c
2
u
3
= c
3
se llaman supercies de coordenadas. La interseccin de estas supercies dene las lneas de coor-
denadas. Especcamente:
{u
2
= c
2
} {u
3
= c
3
} = linea u
1
{u
1
= c
1
} {u
3
= c
3
} = linea u
2
{u
1
= c
1
} {u
2
= c
2
} = linea u
3
si las lneas de coordenadas se cortan ortogonalmente es sistema curvilnea se llama ortogonal.
1
u
3
u
2
u
x
z
y
3 3
c u =
2 2
c u =
1 1
c u =
Ejemplo 7.2 (coordenadas cilndricas)Un punto en el sistema de coordenadas cilndricas se
representa por (, , z) y la relacin con las coordenadas rectangulares est dado por:
x = cos
y = sin
z = z
encontraremos las tres supercies y lneas de coordenadas:
7.3. VECTORES BSICOS 101
Supercie . Haciendo = c
1
se encuentra:
x = c
1
cos
y = c
1
sin
z = z
por tanto x
2
+ y
2
= c
2
1
, por tanto la supercie de coordenadas para es un cilindro generado por
una circunferencia de centro el origen y radio c
1
.
Supercie . Haciendo = c
2
se obtiene:
x = cos c
2
y = sinc
2
z = z
por tanto: y = tan(c
2
) x, por tanto la supercie de coordenadas es un plano que pasa por el origen.
Supercie z. Haciendo z = c
3
, la supercie de coordenadas es un plano paralelo al plano xy.
x
y
z
1
c
1
c
2
1
2 2
c y x = +
x
y
z
( )x c y
2
tan =
y
z
x
3
c z =
7.3 Vectores bsicos
En esta seccin construimos un conjunto de vectores bsicos en el sistema de coordenadas curvilneas
equivalente a la base cannica de R
3
, recordemos que esta base es:
_
i,

j,

k
_
. Partimos del hecho
que cualquier vector r de coordenadas x, y, z se escribe como:
r = x
i +y
j +z
k,
para este n escribimos r = r (u
1
, u
2
, u
3
) . Considrese la lnea u
1
, puesto que la lnea u
1
es la
interseccin de las supercies u
2
= c
2
y u
3
= c
3
, en la lnea u
1
las cooordenadas c
2
y c
3
son
constantes, por tanto el vector tangente para la lnea u
1
es
r
u
1
, sea h
1
=
r
u
1
, luego el vector:
e
1
=
r
u
1
h
1
es un vector unitario tangente en direccin del vector
r
u
1
. Anlogamente se construyen los vectores
unitarios:
e
2
=
r
u
2
h
2
, e
3
=
r
u
3
h
3
donde: h
2
=
r
u
2
, h
3
=
r
u
3
. Los nmeros h
i
, i = 1, 2, 3 se llamarn factores de escala.
Ejemplo 7.3 (Coordenadas cilndricas)Como se sabe las ecuaciones de transformacin de co-
ordenadas cilndricas a rectangulares son:
x = cos
y = sin
z = z
por tanto el vector r = x
i +y
j +z
k se escribe como:
r = cos
i + sin
j +z
k
derivando respectivamente respecto de , y z se obtiene:
r
= cos
i + sin
j
r
= sin
i + cos
j
r
z
=

k
por tanto los factores de escala son:
h
= 1
h
=
h
z
=
r
z
= 1
luego los vectores bsicos son:
e
= cos
i + sin
j
e = sin
i + cos
j
e
z
=

k
x
y
z
e
z
e
2
c =
3
c z =
1
c =
( ) z , ,
plano
plano
cilindro
7.3. VECTORES BSICOS 103
Ejemplo 7.4 Coordenadas esfricas)
x = r sin cos
y = r sin sin
z = r cos
Si r = c
1
, fcilmente se prueba que:
x
2
+y
2
+z
2
= c
2
1
_
familia de esferas
Si = c
2
:
x = r sinc
2
cos
y = r sinc
2
sin
z = r cos c
2
por tanto: x
2
+y
2
= r
2
sin
2
c
2
y z
2
= r
2
cos
2
c
2
, por tanto:
x
2
+y
2
=
_
tan
2
c
2
_
z
2
_
familia de conos
Si = c
3
:
x = r sin cos c
3
y = r sin sinc
3
z = r cos
de donde:
y
x
= tanc
3
, por tanto:
y = (tanc
3
) x} familia de planos
esfera ,
1
c r =
cono ,
2
c =
plano ,
3
c =
x
y
z
e
r
e
Ahora calculamos los vectores bsicos en el sistema de coordenadas esfricas:
r = r sin cos
i +r sin sin
j +r cos
k
r
r
= sin cos
i + sin sin
j + cos
k
r
= r cos cos
i +r cos sin
j r sin
k
r
= r sin sin
i +r sin cos
j
por tanto los elementos de escala son:
h
r
=
r
r
= 1
h
= r
h
= r sin
por tanto:
e
r
= sin cos
i + sin sin
j + cos
k
e
= cos cos
i + cos sin
j sin
k
e
= sin
i + cos
j
Empleando una matriz, lo anterior se escribe como:
_
_
e
r
e
_
_
=
_
_
sin cos sin sin cos
cos cos cos sin sin
sin cos 0
_
_
_
_

i
k
_
_
Ntese que la anterior matriz es ortogonal, es decir su inversa es su transpuesta por tanto:
_
_

i
k
_
_
=
_
_
sin cos cos cos sin
sin sin cos sin cos
cos sin 0
_
_
_
_
e
r
e
_
_
7.4 Gradiente divergencia y rotacional
Si y funcin escalar y

A = A
1
e
1
+ A
2
e
2
+ A
3
e
3
es funcin vectorial en coordenada curvilneas
ortogonales u
1
, u
2
, u
3
, entonces:
=
1
h
1
u
1
e
1
+
1
h
2
u
2
e
2
+
1
h
3
u
3
e
3

A =
1
h
1
h
2
h
3
_
(A
1
h
2
h
3
)
u
1
+
(A
2
h
1
h
3
)
u
2
+
(A
3
h
1
h
2
)
u
3
_

A =
1
h
1
h
2
h
3
h
1
e
1
h
2
e
2
h
3
e
3
u
1
u
2
u
3
h
1
A
1
h
2
A
2
h
3
A
3
7.4. GRADIENTE DIVERGENCIA Y ROTACIONAL 105

Ejercicios
En los siguientes problemas, determinar (a) supercies de coordenadas, gracar. (b) lineas de
coordenadas, gracar. (c) vectores bsicos, gracar. (d) Probar si es o no un sistema ortogonal.
1. Coordenadas cilndricas parablicas (u, v, z).
x =
1
2
_
u
2
v
2
_
, y = uv, z = z
siendo u (, ) , v [0, ) , z (, ) .
2. Coordenadas paraboidales (u, v, )
x = uv cos , y = uv sin, z =
1
2
_
u
2
v
2
_
siendo u [0, ) , v [0, ) , [0, 2] .
3. Coordenadas cilndricas elpticas (u, v, z)
x = acoshucos v, y = asinhusinv, z = z
siendo u [0, ) , v [0, 2] , z (, ) .
4. Coordenas esferoidales alargadas (u, v, )
x = asinhusinv cos , y = asinhusinv sin, z = acoshucos v
siendo: u [0, ) , v [0, 2] , [0, 2] .

Matematicaspara Ing IIISantiago Relos 24 de Mayo 2013

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Matematicaspara Ing IIISantiago Relos 24 de Mayo 2013

Uploaded by

Copyright:

Available Formats

Matemticas para Ingeniera III

Variable Compleja, Anlisis de, Fourier, Anlisis Vectorial

= 1, cada raz tiene el mismo mdulo

(z) existe, se dir que f es diferenciable en z, ms an si f

(z) existe para

(z) g (z) +f (z) g

(z) g (z) f (z) g

(z) = 2 (x + 2) , en el conjunto {z = x +iy : y = x 2}

Ortogonalidad de las funciones seno y coseno

son continuas a pedazos en [a, b] .

k, por tanto la solucin

|f (x)| dx < y es suave a pedazos en cada intervalo

(f (y) cos (wy) dy)

(f (y) sin(wy) dy)

(f (y) cos (wy) dy) cos (wx) +

(f (y) sin(wy) dy) sin(wx)

f (y) cos (wy) dy

f (y) sin(wy) dy,

f (y) cos (wy) dy

|f (x)| < . Calculamos A

f (y) cos (wy) dy

(f (y) cos (wy) dy) cos (wx) +

(f (y) sin(wy) dy) sin(wx)

f (y) [cos (wy) cos (wx) + sin(wy) sin(wx)] dy

f (y) cos (w(y x)) dy dw

|f (u) g (x u)| du < . En estas condiciones la convolucin de

k una funcin vectorial, la divergencia,

k una funcin vectorial, la divergencia, escrito

Denicin 5.6 (Irrotacional) Un campo

k y S la supercie del plano 2x + y = 6

k, y S es parte del paraboloide x

k y S es la parte del paraboloide de ecuacin

k y S es la supercie que encierra el volumen

k y S la regin del plano 2x + 3y + 6z = 12

k y S es la supercie del volmen del

k y S la supercie cerrada del primer octante limitada por y

k y S es la supercie cerrada que consiste

k y S la supercie del volumen limitado

7.4. GRADIENTE DIVERGENCIA Y ROTACIONAL 105

You might also like