Professional Documents
Culture Documents
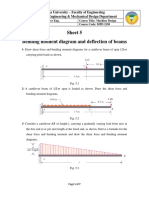
Beams: Bending Stress
Uploaded by
ArifsalimOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Beams: Bending Stress
Uploaded by
ArifsalimCopyright:
Available Formats
1
A. J. Clark School of Engineering Department of Civil and Environmental Engineering A. J. Clark School of Engineering Department of Civil and Environmental Engineering A. J. Clark School of Engineering Department of Civil and Environmental Engineering A. J. Clark School of Engineering Department of Civil and Environmental Engineering A. J. Clark School of Engineering Department of Civil and Environmental Engineering
Third Edition
LECTURE
9
4.1 4.5
4.13
Chapter
BEAMS: BENDING STRESS
by
Dr. Ibrahim A. Assakkaf
SPRING 2003
ENES 220 Mechanics of Materials
Department of Civil and Environmental Engineering
University of Maryland, College Park
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 1
ENES 220 Assakkaf
Beams
Introduction
The most common type of structural
member is a beam.
In actual structures beams can be found in
an infinite variety of
Sizes
Shapes, and
Orientations
2
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 2
ENES 220 Assakkaf
Beams
Introduction
Definition
A beam may be defined as a member whose
length is relatively large in comparison with
its thickness and depth, and which is loaded
with transverse loads that produce significant
bending effects as oppose to twisting or axial
effects
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 3
ENES 220 Assakkaf
Beams
Introduction
Beam
Figure 1
3
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 4
ENES 220 Assakkaf
Beams
Introduction
Figure 2
(a)
(b)
(c)
(d)
a
b
c
d
e
Cable
Load
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 5
ENES 220 Assakkaf
Beams
Introduction
Beams can be
Straight as shown in Figure 1c
For example the straight member bde
Curved as shown in Figure 1c
For example the curved member abc
4
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 6
ENES 220 Assakkaf
Beams
Introduction
Beams are generally classified according
to their geometry and the manner in which
they are supported.
Geometrical classification includes such
features as the shape of the cross section,
whether the beam is
straight or
curved
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 7
ENES 220 Assakkaf
Beams
Introduction
Or whether the beam is
Tapered, or
Has a constant cross section.
And some other features that will be
discussed later
5
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 8
ENES 220 Assakkaf
Beams
Introduction
Beams can also be classified according to
the manner in which they are supported.
Some types that occur in ordinary practice
are shown in Figure 3, the names of some
of these being fairly obvious from direct
observation.
Note that the beams in (d), (e), and (f) are
statically indeterminate.
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 9
ENES 220 Assakkaf
Beams
Introduction
(a) Cantilever
(c) Overhanging
(e) Fixed ended
(b) Simply supported
(d) continuous
(f) Cantilever, simply supported
Figure 3
6
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 10
ENES 220 Assakkaf
Pure Bending
Pure Bending: Prismatic members
subjected to equal and opposite couples
acting in the same longitudinal plane
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 11
ENES 220 Assakkaf
Other Loading Types
Principle of Superposition: The normal
stress due to pure bending may be
combined with the normal stress due to
axial loading and shear stress due to
shear loading to find the complete state
of stress.
Eccentric Loading: Axial loading which
does not pass through section centroid
produces internal forces equivalent to an
axial force and a couple
Transverse Loading: Concentrated or
distributed transverse load produces
internal forces equivalent to a shear
force and a couple
7
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 12
ENES 220 Assakkaf
Symmetric Member in Pure Bending
= =
= =
= =
M dA y M
dA z M
dA F
x z
x y
x x
0
0
These requirements may be applied to the sums
of the components and moments of the statically
indeterminate elementary internal forces.
Internal forces in any cross section are equivalent
to a couple. The moment of the couple is the
section bending moment.
From statics, a couple M consists of two equal
and opposite forces.
The sum of the components of the forces in any
direction is zero.
The moment is the same about any axis
perpendicular to the plane of the couple and
zero about any axis contained in the plane.
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 13
ENES 220 Assakkaf
Normal and Shearing Stress
Normal Stress in beams
The normal stress on plane a-a is related
to the resisting moment M
r
as follows (see
Figure 4):
=
area
dA y M
r
(1)
8
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 14
ENES 220 Assakkaf
Normal and Shearing Stress
Stresses in beams
x
y
b
b
a
a
P
x
y
P
h
w
x
R
M
r
V
O
dA
+y
Figure 4
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 15
ENES 220 Assakkaf
Shearing Stress in beams
The shearing stress on plane a-a is related
to the resisting shear V as follows (see
Figure 4):
=
area
dA V
r
(2)
Normal and Shearing Stress
9
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 16
ENES 220 Assakkaf
Flexural Strains
Deformation of Beam due to Lateral
Loading
w
P
Figure 5
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 17
ENES 220 Assakkaf
Deformation of Beam due to
Lateral Loading
Figure 6
c
Flexural Strains
10
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 18
ENES 220 Assakkaf
Bending Deformations
Beam with a plane of symmetry in pure
bending:
member remains symmetric
bends uniformly to form a circular arc
cross-sectional plane passes through arc center
and remains planar
length of top decreases and length of bottom
increases
a neutral surface must exist that is parallel to the
upper and lower surfaces and for which the length
does not change
stresses and strains are negative (compressive)
above the neutral plane and positive (tension)
below it
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 19
ENES 220 Assakkaf
Strain Due to Bending
Consider a beam segment of length L.
After deformation, the length of the neutral
surface remains L. At other sections,
( )
( )
m x
m
m
x
c
y
c
c
y y
L
y y L L
y L
=
= =
= = =
= = =
=
or
linearly) ries (strain va
11
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 20
ENES 220 Assakkaf
Flexural Strains
Deformation of Beam due to Lateral
Loading
A segment of the beam of Fig. 4 between
planes a-a and b-b is shown in Figure 7
with the deformation (distortion) is greatly
exaggerated
Assumption is made that a plane section
before bending remains plane after
bending.
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 21
ENES 220 Assakkaf
Flexural Strains
Deformation of Beam due to Lateral
Loading
- y
x`
x
y
c
x
y
b
b
a
a
P
x
y
P
h
w
x
R
M
r
V
O
dA
+y
Figure 4
Figure 7
12
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 22
ENES 220 Assakkaf
Stresses in beams
x
y
b
b
a
a
P
x
y
P
h
w
x
R
M
r
V
O
dA
+y
Figure 4
Flexural Strains
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 23
ENES 220 Assakkaf
Flexural Strains
Experimental Results
Precise experimental measures suggest that at
some distance c (see Figure 7) above the bottom
of the beam, longitudinal elements undergo no
change in length.
The curved surface formed by these elements (at
radius ) is referred to as the neutral surface of the
beam, and the intersection of this surface with any
cross section is called the neutral axis of the
section.
13
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 24
ENES 220 Assakkaf
Flexural Strains
Experimental Results
All elements (fibers) on one side of the
neutral surface are compressed and those
on the opposite side are elongated.
In reference to Fig. 8, the fibers above the
neutral surface of the beam are
compressed, while those below the neutral
axis are elongated.
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 25
ENES 220 Assakkaf
Flexural Strains
Experimental Results
- y
x`
x
y
c
dA
+y
Neutral Axis
Figure 8
14
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 26
ENES 220 Assakkaf
Flexural Strains
Longitudinal Strain
The longitudinal strain
x
experienced by a
longitudinal element that is located a
distance y from the neutral axis (surface) of
the beam is determined as follows:
f
i f
x
L
L L
L
L
=
=
L
f
= final length after loading
L
i
= initial length before loading
(3)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 27
ENES 220 Assakkaf
Flexural Strains
Longitudinal Strain
From the geometry of the beam as shown
in Figure 7 and 8:
- y
x`
x
y
c
( )
=
=
y
x
x x
x
(4)
15
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 28
ENES 220 Assakkaf
Flexural Strains
Longitudinal Strain
( )
y
y y
y
x
x x
x
x
1
=
=
(5)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 29
ENES 220 Assakkaf
Flexural Strains
Longitudinal Strain
The normal longitudinal strain
x
varies
linearly, through the member, with the
distance y from the neutral surface, and it
is given by
y
x
=
(6)
16
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 30
ENES 220 Assakkaf
Flexural Stress
For special case of linearly elastic
deformation, the relationship between
the normal stress
x
and the normal
strain
x
is given by Hookes law as
slope = =
x
x
E
x
slope = =
x
x
E
(7)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 31
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Eq. 7 can be rewritten as
Recall Eq. (6) , therefore
E
x x
= (8)
y
x
=
E
y
E
x x
= =
(9)
17
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 32
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Distribution of Normal Stress in a Beam Cross
Section
x
y
P
w
R
F
C
F
T
V
r
c
y
dy
y
C
dA
Neutral axis
Figure 9
Centroidal axis
c c
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 33
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
The resisting moment M
r
that can be
develop by the normal stress in a typical
beam with loading in a plane of symmetry
but arbitrary cross section (Fig. 9) is given
by Eq. 1 as
=
area
dA y M
x r
18
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 34
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Since y is measured from the neutral axis
(surface), it is necessary to locate this axis
by means of the equilibrium equation as
follows:
0
0
=
=
dA
F
A
x
x
(10)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 35
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Substituting for
x
given by Eq. 9 into Eq.
10, yields
But
0 = =
=
A
A A
x
ydA
E
EdA
y
dA
) ( axis centroidal to
axis neutral from distance
c-c
ydA y
A
C
= =
(11)
(12)
19
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 36
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Therefore, Eq. 11 becomes
Since neither (E/) nor A are zero, y
C
must
equal zero.
0 = =
A y
E
dA
C
A
x
(12)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 37
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
For flexural loading and linearly
elastic action, the neutral axis passes
through the centroid of the cross section
of the beam
20
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 38
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
The maximum normal stress on the cross
section is given by
Combining Eqs. 9 and 13, hence
c
E
=
max (13)
c x
c
y
c
y
= =
max
(14)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 39
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Substituting Eq. 14 into Eq. 1, gives
The integral is called the second
moment of area, and it is given the
symbol I.
=
=
A
c
A
c
x r
dA y
c
dA
c
y
y
dA y M
2
area
dA y
2
(15)
21
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 40
ENES 220 Assakkaf
Flexural Stress
Flexural Normal Stress
Substituting for the second moment of area
I of the cross section of the beam into Eq.
15, yields
max c
2
or
= =
= =
c
I
M
I
c
dA y
c
M
r
c
A
c
r
(16)
(17)
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 41
ENES 220 Assakkaf
Elastic Flexural Formula
The elastic flexural formula for normal
stress is given by
I
y M
I
c M
r
x
r
=
=
and
max
(18)
(19)
22
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 42
ENES 220 Assakkaf
Elastic Flexural Formula
An alternative form of the flexural
formula for maximum normal stress is
given by
Where
S
M
r
=
max
(20)
c
I
S =
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 43
ENES 220 Assakkaf
Stress Due to Bending
For a linearly elastic material,
linearly) varies (stress
m
m x x
c
y
E
c
y
E
=
= =
For static equilibrium,
=
= = =
dA y
c
dA
c
y
dA F
m
m x x
0
0
First moment with respect to neutral
plane is zero. Therefore, the neutral
surface must pass through the
section centroid.
For static equilibrium,
I
My
c
y
S
M
I
Mc
c
I
dA y
c
M
dA
c
y
y dA y M
x
m x
m
m m
m x
=
=
= =
= =
= =
ng Substituti
2
23
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 44
ENES 220 Assakkaf
Deformation in a Symmetric
Member in Pure Bending
Deformation due to bending moment M is
quantified by the curvature of the neutral surface
EI
M
I
Mc
Ec Ec c
m m
=
= = =
1 1
Although cross sectional planes remain planar
when subjected to bending moments, in-plane
deformations are nonzero,
y y
x z x y
= = = =
Expansion above the neutral surface and
contraction below it cause an in-plane curvature,
curvature c anticlasti
1
= =
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 45
ENES 220 Assakkaf
Example 1
A cast-iron machine part is acted upon
by a 3 kN-m couple. Knowing E = 165
GPa and neglecting the effects of
fillets, determine (a) the maximum
tensile and compressive stresses, (b)
the radius of curvature.
SOLUTION:
Based on the cross section geometry,
calculate the location of the section
centroid and moment of inertia.
( ) + =
=
2
d A I I
A
A y
Y
x
Apply the elastic flexural formula to
find the maximum tensile and
compressive stresses.
I
Mc
m
=
Calculate the curvature
EI
M
=
1
24
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 46
ENES 220 Assakkaf
Example 1 (contd)
SOLUTION:
Based on the cross section geometry, calculate
the location of the section centroid and
moment of inertia.
mm 38
3000
10 114
3
=
=
A
A y
Y
= =
=
=
3
3
3
3 2
10 114 3000
10 4 2 20 1200 30 40 2
10 90 50 1800 90 20 1
mm , mm , mm Area,
A y A
A y y
( ) ( )
( ) ( )
4 9 - 3
2 3
12
1 2 3
12
1
2 3
12
1 2
m 10 868 mm 10 868
18 1200 40 30 12 1800 20 90
= =
+ + + =
+ = + =
I
d A bh d A I I
x
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 47
ENES 220 Assakkaf
Example 1 (contd)
Apply the elastic flexural formula to find the
maximum tensile and compressive stresses.
4 9
4 9
mm 10 868
m 038 . 0 m kN 3
mm 10 868
m 022 . 0 m kN 3
= =
= =
=
I
c M
I
c M
I
Mc
B
B
A
A
m
MPa 0 . 76 + =
A
MPa 3 . 131 =
B
Calculate the curvature
( )( )
4 9 -
m 10 868 GPa 165
m kN 3
1
=
=
EI
M
m 7 . 47
m 10 95 . 20
1
1 - 3
=
=
25
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 48
ENES 220 Assakkaf
Unsymmetrical Bending
Analysis of pure bending has been limited
to members subjected to bending couples
acting in a plane of symmetry.
Will now consider situations in which the
bending couples do not act in a plane of
symmetry.
In general, the neutral axis of the section will
not coincide with the axis of the couple.
Cannot assume that the member will bend
in the plane of the couples.
The neutral axis of the cross section
coincides with the axis of the couple
Members remain symmetric and bend in
the plane of symmetry.
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 49
ENES 220 Assakkaf
Unsymmetrical Bending
Wish to determine the conditions under
which the neutral axis of a cross section
of arbitrary shape coincides with the
axis of the couple as shown.
couple vector must be directed along
a principal centroidal axis
inertia of product I dA yz
dA
c
y
z dA z M
yz
m x y
= =
= =
0 or
0
The resultant force and moment
from the distribution of
elementary forces in the section
must satisfy
couple applied M M M F
z y x
= = = = 0
neutral axis passes through centroid
= =
dA y
dA
c
y
dA F
m x x
0 or
0
defines stress distribution
inertia of moment I I
c
I
dA
c
y
y M M
z
m
m z
= = =
= =
M or
26
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 50
ENES 220 Assakkaf
Unsymmetrical Bending
Superposition is applied to determine stresses in
the most general case of unsymmetric bending.
Resolve the couple vector into components along
the principle centroidal axes.
sin cos M M M M
y z
= =
Superpose the component stress distributions
y
y
z
z
x
I
y M
I
y M
+ =
Along the neutral axis,
( ) ( )
tan tan
sin cos
0
y
z
y z y
y
z
z
x
I
I
z
y
I
y M
I
y M
I
y M
I
y M
= =
+ = + = =
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 51
ENES 220 Assakkaf
Unsymmetrical Bending
The form of the flexural formula for
normal stress in unsymmetrical bending
is given by
Where
(21)
y
y
z
z
x
I
y M
I
y M
+ =
M
z
, I
z
= moment and moment of inertia about z-axis
M
y
, I
y
= moment and moment of inertia about z-axis
27
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 52
ENES 220 Assakkaf
Example 2
A 1600 lb-in couple is applied to a
rectangular wooden beam in a plane
forming an angle of 30 deg. with the
vertical. Determine (a) the maximum
stress in the beam, (b) the angle that the
neutral axis forms with the horizontal
plane.
SOLUTION:
Resolve the couple vector into
components along the principle
centroidal axes and calculate the
corresponding maximum stresses.
sin cos M M M M
y z
= =
Combine the stresses from the
component stress distributions.
y
y
z
z
x
I
y M
I
y M
+ =
Determine the angle of the neutral
axis.
tan tan
y
z
I
I
z
y
= =
LECTURE 9. BEAMS: BENDING STRESS (4.1 4.5, 4.13) Slide No. 53
ENES 220 Assakkaf
Example 2 (contd)
Resolve the couple vector into components and calculate
the corresponding maximum stresses.
( )
( )
( )( )
( )( )
( )( )
( )( )
psi 5 . 609
in 9844 . 0
in 75 . 0 in lb 800
along occurs to due stress nsile largest te The
psi 6 . 452
in 359 . 5
in 75 . 1 in lb 1386
along occurs to due stress nsile largest te The
in 9844 . 0 in 5 . 1 in 5 . 3
in 359 . 5 in 5 . 3 in 5 . 1
in lb 800 30 sin in lb 1600
in lb 1386 30 cos in lb 1600
4
2
4
1
4 3
12
1
4 3
12
1
=
= =
=
= =
= =
= =
= =
= =
y
y
z
z
z
z
y
z
y
z
I
z M
AD M
I
y M
AB M
I
I
M
M
The largest tensile stress due to the combined loading
occurs at A.
5 . 609 6 . 452
2 1 max
+ = + = psi 1062
max
=
y
y
z
z
x
I
y M
I
y M
+ =
You might also like
- Shafts and RotationDocument29 pagesShafts and RotationjeeveshprasoonNo ratings yet
- Shear in Beams: FALL 2002Document22 pagesShear in Beams: FALL 2002SSNo ratings yet
- Biaxial BendingDocument15 pagesBiaxial Bendingstylistik0% (1)
- Columns: Buckling (Pinned Ends)Document29 pagesColumns: Buckling (Pinned Ends)Michelle MedinaNo ratings yet
- 5a PDFDocument33 pages5a PDFJoey Calda Jr.No ratings yet
- Mechanics of MaterialsDocument21 pagesMechanics of MaterialsUbaid Ahmed Mughal100% (1)
- Thin-Walled Pressure Vessels PDFDocument18 pagesThin-Walled Pressure Vessels PDFtunglq0411No ratings yet
- Lab ReportDocument20 pagesLab ReportJoshua Reynolds67% (3)
- Columns 1Document16 pagesColumns 1ShahriazSAMNo ratings yet
- AD 293 - Web Panel Zones in Vierendeel Girders (Part 1)Document2 pagesAD 293 - Web Panel Zones in Vierendeel Girders (Part 1)symon ellimacNo ratings yet
- Chapter 7Document30 pagesChapter 7momanonaNo ratings yet
- Analysis of Industrial Steel BuildingDocument20 pagesAnalysis of Industrial Steel BuildingVeera SundarNo ratings yet
- Cable Element Analysis TechniquesDocument16 pagesCable Element Analysis TechniquesPankaj_Taneja_9684No ratings yet
- 4281 - 03 Stiffened Shear WebDocument26 pages4281 - 03 Stiffened Shear WebAndrew GilbrideNo ratings yet
- Combined LoadingDocument23 pagesCombined LoadingAbhishek DwivediNo ratings yet
- Rigid Frame Analysis and DesignDocument12 pagesRigid Frame Analysis and Designdarebusi1No ratings yet
- Determinate beams and frames analysisDocument35 pagesDeterminate beams and frames analysisColin MacDougallNo ratings yet
- CHAPTER V Engineering Mechanics-I 2015Document16 pagesCHAPTER V Engineering Mechanics-I 2015nvnrevNo ratings yet
- SteelDesign Flexural FuDocument6 pagesSteelDesign Flexural FunotevaleNo ratings yet
- Columns and Struts: Failure Analysis and Design FormulasDocument10 pagesColumns and Struts: Failure Analysis and Design FormulasAshish KumarNo ratings yet
- Bending Stresses in BeamDocument29 pagesBending Stresses in BeamilhammkaNo ratings yet
- Design of tension members and splicesDocument7 pagesDesign of tension members and splicesSourabh SrivastavaNo ratings yet
- 13 1108 PDFDocument14 pages13 1108 PDFMohan KumarNo ratings yet
- Bending Stresses in Beams: Jishnu V Engineer BhelDocument29 pagesBending Stresses in Beams: Jishnu V Engineer Bhelmulikamol5No ratings yet
- Design of Flexural MembersDocument20 pagesDesign of Flexural MembersSathish SelvaNo ratings yet
- Lateral Stability of Long Prestressed Concrete Beams - Part 1Document20 pagesLateral Stability of Long Prestressed Concrete Beams - Part 1TaiCheong LeeNo ratings yet
- Beam Deflection Calculation MethodsDocument3 pagesBeam Deflection Calculation MethodsAGEGTAMNo ratings yet
- MARA University of Technology Faculty of Mechanical EngineeringDocument12 pagesMARA University of Technology Faculty of Mechanical EngineeringAdiela Syuhada Roslan100% (1)
- Castigliano's Second Theorem ProblemsDocument3 pagesCastigliano's Second Theorem Problemsrohit kumarNo ratings yet
- Chapter-8 Flexural Stress in BeamsDocument28 pagesChapter-8 Flexural Stress in BeamsShantanu PaulNo ratings yet
- Shear in Thin WalledDocument12 pagesShear in Thin WalledbenNo ratings yet
- Lecture # 1: 1. ColumnDocument8 pagesLecture # 1: 1. ColumnShijumon KpNo ratings yet
- Design Analysis Beam ACI PDFDocument48 pagesDesign Analysis Beam ACI PDFAlbert DimayugaNo ratings yet
- CE 3100: Structural Engineering Lab: February 4Document12 pagesCE 3100: Structural Engineering Lab: February 4Sarankumar ThathuruNo ratings yet
- Sheet 5Document7 pagesSheet 5Mustafa AymanNo ratings yet
- 7.2 Short Columns Axially LoadedDocument28 pages7.2 Short Columns Axially Loadedqaxu xuxuNo ratings yet
- ESQUEMAS UNIONES MetalicasDocument165 pagesESQUEMAS UNIONES MetalicasGuillermo Hortigüela Cordoba100% (6)
- Final Structure LabDocument38 pagesFinal Structure LabNurul Syuhada0% (1)
- Bending Stresses in BeamDocument29 pagesBending Stresses in BeamilhammkaNo ratings yet
- Theory of structure microprojectDocument5 pagesTheory of structure microprojectXyz AvmcNo ratings yet
- Built Up ColumnsDocument22 pagesBuilt Up Columnsfinn.crown100% (1)
- Structural Mechanics: Department of Civil EngineeringDocument8 pagesStructural Mechanics: Department of Civil EngineeringMuhammad AsadNo ratings yet
- Anclaje MurosDocument7 pagesAnclaje MurosPatricio LazcanoNo ratings yet
- Ch3 FrameDocument51 pagesCh3 Framengkt722No ratings yet
- AISC Part3 Tension Member Design 1697301566Document16 pagesAISC Part3 Tension Member Design 1697301566kfupgessytogimmbhmNo ratings yet
- Module 3 and 5 PDFDocument55 pagesModule 3 and 5 PDFSaptadip SahaNo ratings yet
- Helical Pipe Heat Exchanger Modeling FEADocument15 pagesHelical Pipe Heat Exchanger Modeling FEAUsama ArifNo ratings yet
- Laced and Battened ColumnsDocument29 pagesLaced and Battened ColumnsAbdullahi Dirie AbdiNo ratings yet
- Exp 6Document4 pagesExp 6Ah ChaiNo ratings yet
- Chapter 07Document35 pagesChapter 07Hassan SaeedNo ratings yet
- Section 09 - Spiral ColumnDocument8 pagesSection 09 - Spiral ColumnmagdyamdbNo ratings yet
- FERDIN 1 (1) - Removed - Removed (1) - RemovedDocument3 pagesFERDIN 1 (1) - Removed - Removed (1) - RemovedGildardo VillalpbosNo ratings yet
- Basic Theory of Structures: The Commonwealth and International Library: Mechanical Engineering DivisionFrom EverandBasic Theory of Structures: The Commonwealth and International Library: Mechanical Engineering DivisionRating: 4 out of 5 stars4/5 (4)
- Strength of Materials: An Introduction to the Analysis of Stress and StrainFrom EverandStrength of Materials: An Introduction to the Analysis of Stress and StrainRating: 5 out of 5 stars5/5 (1)
- Pressure Vessel and Stacks Field Repair ManualFrom EverandPressure Vessel and Stacks Field Repair ManualRating: 4 out of 5 stars4/5 (4)
- Strength of Materials: Theory and ExamplesFrom EverandStrength of Materials: Theory and ExamplesRating: 4.5 out of 5 stars4.5/5 (13)
- Mitigation of Alkali-Silica Reaction While Using Highly Reactive Aggregates With Class C Fly Ash and Reduction in Water To Cementitious RatioDocument6 pagesMitigation of Alkali-Silica Reaction While Using Highly Reactive Aggregates With Class C Fly Ash and Reduction in Water To Cementitious RatioArifsalimNo ratings yet
- Concrete Silo DesignDocument19 pagesConcrete Silo DesignSnehendu Biswas50% (2)
- Seismic Analysis of G+5 Framed Structures With and Without Floating Columns Using ETABS-2013 SoftwareDocument8 pagesSeismic Analysis of G+5 Framed Structures With and Without Floating Columns Using ETABS-2013 SoftwareArifsalimNo ratings yet
- Drainage Design GuidelinesDocument144 pagesDrainage Design GuidelinesriefsaldyNo ratings yet
- Silos Ensilage and Silage 1889 From WWW Jgokey ComDocument120 pagesSilos Ensilage and Silage 1889 From WWW Jgokey ComArifsalimNo ratings yet
- Storage TanksDocument304 pagesStorage Tanksmohamedyoussef1100% (30)
- Solids Notes 10 Hopper DesignDocument26 pagesSolids Notes 10 Hopper Designellantidinesh100% (1)
- Bulk Solids HandlingDocument303 pagesBulk Solids HandlingDr_M_Soliman100% (12)
- Structural Design of Steel Bins and SilosDocument36 pagesStructural Design of Steel Bins and Silosyoussefayay92% (12)
- Silo PDFDocument6 pagesSilo PDFdjsmoniNo ratings yet
- Eurocode Load Combinations For Steel Structures 2010Document29 pagesEurocode Load Combinations For Steel Structures 2010Aram Chtchyan73% (11)
- Seismic Retrofitting of Existing StructuresDocument111 pagesSeismic Retrofitting of Existing StructuresrealchicNo ratings yet
- A Practical Proposal For Seismic Isolation Design AgainstDocument8 pagesA Practical Proposal For Seismic Isolation Design AgainstArifsalimNo ratings yet
- 1742Document52 pages1742Swapnesh MhatreNo ratings yet
- 3D seismic analysis of multi-storey wood framesDocument8 pages3D seismic analysis of multi-storey wood framesArifsalimNo ratings yet
- Seismic Isolation Design RequirementsDocument51 pagesSeismic Isolation Design RequirementsArifsalimNo ratings yet
- International Code Council 2012/2013 Code Development Cycle Group A (2012)Document352 pagesInternational Code Council 2012/2013 Code Development Cycle Group A (2012)ArifsalimNo ratings yet
- INTERLOCK - Lafarge in Kenya - Cement, Concrete, AggregatesDocument2 pagesINTERLOCK - Lafarge in Kenya - Cement, Concrete, AggregatesArifsalimNo ratings yet
- Eurocodes Worked ExamplesDocument185 pagesEurocodes Worked ExamplesPaskal Drazhich100% (8)
- Earthquake Resistant Construction HandbookDocument17 pagesEarthquake Resistant Construction HandbookArifsalimNo ratings yet
- International Code Council 2012/2013 Code Development Cycle Group A (2012)Document352 pagesInternational Code Council 2012/2013 Code Development Cycle Group A (2012)ArifsalimNo ratings yet
- Comparison of New Zealanda Standards Used For Seismic Design of Concrete BuildingsDocument17 pagesComparison of New Zealanda Standards Used For Seismic Design of Concrete Buildingshm20284No ratings yet
- Airport Pavement Design GuidanceDocument124 pagesAirport Pavement Design GuidanceJim Jakson MboeNo ratings yet
- Apex Steel Catalogue PDFDocument16 pagesApex Steel Catalogue PDFArifsalim0% (1)
- Seismic Design of Reinforced Concrete Special Moment FramesDocument31 pagesSeismic Design of Reinforced Concrete Special Moment FrameswilfredNo ratings yet
- Airport Pavement Design GuidanceDocument124 pagesAirport Pavement Design GuidanceJim Jakson MboeNo ratings yet
- Cement Consistency and Setting Times Test ReportDocument5 pagesCement Consistency and Setting Times Test Reportvelmurug_balaNo ratings yet
- Portal MethodDocument10 pagesPortal MethodDoer_91No ratings yet
- 0.04 Roof and Stormwater3 PDFDocument6 pages0.04 Roof and Stormwater3 PDFArifsalimNo ratings yet
- X HVB Specification PDFDocument52 pagesX HVB Specification PDFAnonymous 6aGAvbNNo ratings yet
- Comflor Composite Floor Deck Brochure UK PDFDocument32 pagesComflor Composite Floor Deck Brochure UK PDFJoeNo ratings yet
- Potres ZidoviDocument23 pagesPotres ZidoviIvan KelamNo ratings yet
- Bracing Connection Work Point PDFDocument2 pagesBracing Connection Work Point PDFaams_sNo ratings yet
- Slope - Deflection Method (Beams) : Fem) PL Fem) PLDocument9 pagesSlope - Deflection Method (Beams) : Fem) PL Fem) PLAngelica FabianNo ratings yet
- CVEN3302 Structural Steel DesignDocument404 pagesCVEN3302 Structural Steel Designhas960100% (12)
- BCM Assignment Group 8Document18 pagesBCM Assignment Group 8Ashrutha HarshiniNo ratings yet
- Stress Analysis SummaryDocument8 pagesStress Analysis SummaryMohammed Taher100% (1)
- Engineering Civil Structures - HSCDocument335 pagesEngineering Civil Structures - HSChr_kapani100% (1)
- Rectangular Tanks: A Primer on Design and ConstructionDocument7 pagesRectangular Tanks: A Primer on Design and Constructionfawmer61No ratings yet
- Performance of Various Types of Buildings During EarthquakeDocument5 pagesPerformance of Various Types of Buildings During EarthquakeSyed Mohd Mehdi100% (1)
- Bar Hypermesh TutorialDocument14 pagesBar Hypermesh TutorialDev Kumar DevaNo ratings yet
- Reinforced Concrete Design Formulas Based on Reinforcement RatiosDocument23 pagesReinforced Concrete Design Formulas Based on Reinforcement RatiosNaveenkumarNo ratings yet
- Projek Math FatahDocument15 pagesProjek Math FatahAbdul Fatah NajmiNo ratings yet
- Analysis and Design of Beams For Bending: MEE 320: Strength of MaterialsDocument36 pagesAnalysis and Design of Beams For Bending: MEE 320: Strength of Materialskamalnath100% (1)
- Collapse of Hotel New World - SingaporeDocument71 pagesCollapse of Hotel New World - SingaporePriyam AndhariaNo ratings yet
- SyllabusDocument52 pagesSyllabusgururajNo ratings yet
- Management of Highway StructuresDocument297 pagesManagement of Highway Structureswildfire11No ratings yet
- Jib TextDocument36 pagesJib Textluiscremaschi100% (2)
- Civil Engineering Beam Deflection CalculationDocument21 pagesCivil Engineering Beam Deflection CalculationNajmi AimanNo ratings yet
- Tagore Ansys Record Mar' 2021 - TECDocument40 pagesTagore Ansys Record Mar' 2021 - TECVijay RamanathanNo ratings yet
- Ros Example PDFDocument30 pagesRos Example PDFdoutorNo ratings yet
- Span Thickness Limits For Deflection ControlDocument8 pagesSpan Thickness Limits For Deflection Controlf81lNo ratings yet
- Planning Manual: LCT SystemDocument40 pagesPlanning Manual: LCT System唐鹏飞No ratings yet
- Syllabus - B.E. Mechanical - 2009 RegulationDocument161 pagesSyllabus - B.E. Mechanical - 2009 RegulationshivakumarNo ratings yet
- Modeling and Control of Flexible Link Robots - 48628966Document153 pagesModeling and Control of Flexible Link Robots - 48628966GIYEONGNo ratings yet
- 220 3DR S15 00001 SiDocument48 pages220 3DR S15 00001 SiJDGM01No ratings yet
- Example Design by Hand Creep Shrinkage TemperaturesDocument17 pagesExample Design by Hand Creep Shrinkage TemperaturestarekhocineNo ratings yet
- Syllarch 1 10Document92 pagesSyllarch 1 10Paan Tapari Vala HariNo ratings yet
- Structural Notes PDFDocument158 pagesStructural Notes PDFAin ZulkefliNo ratings yet