Professional Documents
Culture Documents
01 Shell Balance Problem With Newton S Law
Uploaded by
vijayOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
01 Shell Balance Problem With Newton S Law
Uploaded by
vijayCopyright:
Available Formats
1
Outline of ta3220 - opening lectures 1. laminar flow of Newtonian and non-Newtonian fluids A. Fluid properties: Newtonian fluids 1. thought experiment defining viscosity 2. magnitudes of viscosity; trends with T, p 3. Newton's law in FTI 4. meaning of shear stress in tensor form 5. how one can measure viscosity without infinite plates B. shell-balance problems for Newtonian fiuids in laminar fiow 1. procedure (cf. also Sect. 5.6 of FTI) 2. examples in FTI a. shear fiow between parallel plates - no pressure or gravity driving force b. flow in a slit - no pressure driving force c. fiow in a tube - no gravity driving force d. film condensation (falling film) 3. examples from ^iSZ a. falling film b. fiow in a tube (both pressure and gravity) c. flow in an annulus (both pressure and gravity) d. fiow in a slit (both pressure and gravity) - only final equation given 4. limits to laminar fiow in terms of Re C. shell-balance problems for non-Newtonian fluids 1. properties of non-Newtonian fiuids a. Bingham plastic (beware of how i^77 writes this equation!) b. power-law fiuid c. effective viscosity for a non-Newtonian fiuid 2. flow derivations a. flow of Bingham plastic in tube b. power-law fluid in a tube c. definition of effective viscosity for tube flow d. flow in a slit i. Newtonian fluid reconsidered ii. Bingham plastic iii. power-law fluid e. non-Newtonian fluids in an annulus 3. cf, derivations in FTI a. Bingham plastic in slit (only gravity, no pressure driving force) b. power-law fluid in slit (no pressure driving force) 4. conditions for suspending solid particles in Bingham plastic
L Laminar flow of Newtonian and non-Newtonian fluids A. Fluid properties: Newtonian fluid 1. Thought experiment
F/A =
Py ,x
=T
*^ y.\
Units: SI unit of viscosity: Pa s
2. Magnitudes of viscosity
3. Newton's law in FTI (see Eq. 2.4)
Trends of viscosity with t, p for pure, single-component liquids:
for gases:
for cmde oils with dissolved gas
4. Meaning of shear stress in tensor form
yx
his
FINITE PARALLEL P L A T E S A R E IMPOSSIBLE, OF C O U R S E .
THEN HOW CAN ONE MEASURE V I S C O S I T Y ?
USING CONCENTRIC CYLINDERS. IF GAP WIDTH-^0 GAP APPROXIMATES PLANAR G E O M E T R Y .
IF GAP WIDTH -hO, NEED CORRECTION F A C T O R S
. . . THE IDEA BEHIND "FANN" VISCOMETER
-5^. Q>,^ outline of shell momentum balance approach (BSL ch. 2)
Procedure: ( c / B S L section 2.1)
1. SELECT COORDINATE SYSTEM; DEFINE CONTROL V O L U M E 2. STATE B O U N D A R Y CONDITIONS * 3. 4. a) 5. PERFORM M O M E N T U M B A L A N C E * * TfflCICNESS ^ 0 (-^ dif. eq. for x) (optional): solve dif. eq. for i , apply b.c. - IF b.c. applies to x alone R E L A T E x TO dv/dx (apply constitutive equation)
6. SOLVE DIF. EQ. FOR v; APPLY B.C. * a) (optional) COMPUTE w (mass rate o f flow), etc.
^ B O U N D A R Y CONDITIONS ( c / B S L section 2.1)
1. SPECIFY V AT SOLID SURFACE la) FLUID V = SOLID VELOCITY AT SOLID WALL 2. SPECIFY X AT FLUID SURFACE 2a) I N LIQUID, x - 0 AT GAS LF. 2b) X, V CONTINUOUS ACROSS LIQUID/LIQUID LF. 3. T V N O T TT^JFTNTTE ANYAVHERE WITHIN CONTROL VOLUME
''ALL BOUNDARY CONDITLONS ARISE FROM (i.e., from problem statement) NATURE''
E L E M E N T S OF M O M E N T U M B A L A N C E
MOMENTUM FLUX ( a area); called "(j)" tensor in BSL (sect. 1.7) 1. CONVECTION OF MOMENTUM THRU SURFACE (pvv) 2. SHEAR STI^SS x ON SURFACE ("molecular transport o f
momentum")
3. PRESSURE PRESSING INWARD ON SURFACE-p MOMENTUM "GENERATION" or "SOURCE" ( a volume) 4. BODY FORCES WITHIN VOLUME MOMENTUM ACCUMULATION (a volume) (not at steady state!) 5. ACCELERATION OF SYSTEM MASS - d(p v)/at
L B . 1. continued Key elements in shell balances:
2. Notes on examples in FTI
An alternate derivation for Vz(r): The derivation of Vz(r) for Newtonian flow in an annulus in BSL section 2.4 malces use of a clever change of variable in equation 2.4-3. Most students (and probably most professors) would not thinlc of making this change. It is not necessary for solving this problem. You should be able to solve tliis problem by the straight-ahead method illustrated here. The equation numbers here, after 2.4-2, have no particular relation to the equation numbers ui section 2.4. Start with equation 2.4-2:
rn
2L
r +
J
}
(2.4-2)
Equate v from Newton's law of viscosity witli \ r dv. C
from the momentum balance:
(2.4-3 a)
2L
r
- P
~dr
rP
dr
V
V
2juL
\
r r
2
/Jr
(2.4-4a)
2juL J 2
9l Inr + C,
(2.4-5a)
B.C.: v. = Oatr = R
(2.4-6a)
9i In i? + C
PQ-PL
\
J
(2.4-7a)
P,-PL
"R'
2jLlL J 2
CI
Ini?
(2.4-8a)
inserting this into Eq. 2.4-^a gives
P -P R 1 2
\
\
+^lnf^
(2.4-9a)
B.C.: v, = Oatr = KR
\
(2.4-1 Oa)
\2
2 /zI
R 1 2
0
R K
(2.4-1 la)
V 2juL
(2.4-12a)
c
In
2/zZ.
(2.4-13 a)
Plug this expression for C] into Eq. 2.4-9a:
\
r P - P R 1 2/JL 2
\
VR
In
/ 1 N 2/JL 1
2 J
1 In
J
\
Group terms together with common factor:
P - P
\
A/JL
R 1
r V l TP.-P. 0 L
J
R R'hi r
1 1 In K
. \2
4/JL
1
J
RJ
K In R\ /1 > rJ 1 In
This is Eq. 2.4-14 of BSL.
fflL Fa AsssBBipDODDS BeDsDid Beirwatnoffiis D B D B I L Cl!fi=
C-
" o
"slov//' rectilinear flow (except fiow around sphere) incompressible (p constant^ Newtonian (p. constant) floid steady state (v(x) indegeodesi of t) ignore entrance and exit effects no slip at walls (v = wall velocity at wall; "BC type 1") fluid = continuum
I
Assumptions break down when flow too fast: "turbulence" Quantify conditions for breakdown in "Reynolds number:" Re (iength)(velocity)(density) viscosity Def. of Re
YVp
inertial effects viscous
2 pV
(fiV/L)
Type of Flow
Horizontal J infinite plates (BSL Fig. 1.1-1) Falling Film
Trans, to turbulence
3000
Reference
Schlicliting, Boundary Layer Theory, 1979, p. 590
4S<Vz>p
20
SL, p. 46
45 <
>p
2300
Wliite, Fluid Mechanics 1979, p. 433
Circular Tube 2 (R-icR) V p
2100
BSL, p. 52
Annulus
2000
BSL, p. 56
Flow Ai'ound Sphere ^ computed
0.1 1*
BSL, p. 61
= VA is within about 10% of true value for Re < 1
These values apply only to Newtonian Fluids!
You might also like
- Finite Element Simulation of Dip Coating, I - Newtonian FluidsDocument17 pagesFinite Element Simulation of Dip Coating, I - Newtonian FluidsLindsay SchneiderNo ratings yet
- Fulltext PDFDocument7 pagesFulltext PDFMuhammad FarooqNo ratings yet
- Settlingvelocitiesofparticulatesystems PDFDocument36 pagesSettlingvelocitiesofparticulatesystems PDFneuro astroNo ratings yet
- Field Observations of Wave-Induced Porewater PressuresDocument14 pagesField Observations of Wave-Induced Porewater PressuresRIOS TSENGNo ratings yet
- Fluid Mech ModuleDocument66 pagesFluid Mech ModuleVudayagirisivaNo ratings yet
- Exam SolutionsDocument11 pagesExam SolutionsLacey Prestwood100% (1)
- The Vortical Flow Above The Drain-Hole in A Rotating VesselDocument32 pagesThe Vortical Flow Above The Drain-Hole in A Rotating VesselRonaldo Spielberg100% (1)
- 1 s2.0 S0167564802800971 MainDocument8 pages1 s2.0 S0167564802800971 MainRicardo SilvaNo ratings yet
- The Geotechnics of Real Materials: The <INF>g</INF><INF>k</INF> MethodFrom EverandThe Geotechnics of Real Materials: The <INF>g</INF><INF>k</INF> MethodNo ratings yet
- Two Phase Flow, Rheology and Powder Flow: Chapters 6, 9 & 10 in FundamentalsDocument44 pagesTwo Phase Flow, Rheology and Powder Flow: Chapters 6, 9 & 10 in FundamentalsUmesh PatelNo ratings yet
- Stokes Second Problem by Laplace TransformDocument19 pagesStokes Second Problem by Laplace TransformSidra AfzalNo ratings yet
- Model 1Document68 pagesModel 1Prashanth Menon0% (1)
- Studies On Bubble DynamicsDocument10 pagesStudies On Bubble Dynamicsvishnu cNo ratings yet
- Experiment (1) : Hydrostatic Force On A Plane Surface: ObjectivesDocument25 pagesExperiment (1) : Hydrostatic Force On A Plane Surface: ObjectivesBatool Al-kharabshehNo ratings yet
- Physico-Chemistry of Solid-Gas Interfaces: Concepts and Methodology for Gas Sensor DevelopmentFrom EverandPhysico-Chemistry of Solid-Gas Interfaces: Concepts and Methodology for Gas Sensor DevelopmentNo ratings yet
- Surface TensionDocument5 pagesSurface TensionEntropy ChannelNo ratings yet
- Taylor GalerkinDocument16 pagesTaylor GalerkinAlaa AskNo ratings yet
- Mec 214 Fluid Mechanics PracticalxDocument51 pagesMec 214 Fluid Mechanics PracticalxVietHungCao0% (1)
- Stability of Bodewadt FlowDocument8 pagesStability of Bodewadt FlowAmmara RaoNo ratings yet
- Metallurgical Effects On The Dynamic of Hydrogen Loading in PDDocument4 pagesMetallurgical Effects On The Dynamic of Hydrogen Loading in PDalienslagNo ratings yet
- Hydrodynamic Impact Numerical and Experimental InvestigationsDocument27 pagesHydrodynamic Impact Numerical and Experimental InvestigationsAdam LewisNo ratings yet
- Lockhart and Martinelli Launched Two Basic Postulates For TheirDocument4 pagesLockhart and Martinelli Launched Two Basic Postulates For Theirsatish MotkulwadNo ratings yet
- MTWS5 01 TomiyamaxxxxxxxxxxxxxxDocument17 pagesMTWS5 01 Tomiyamaxxxxxxxxxxxxxxhamza aouaichiaNo ratings yet
- Study On Wave Calculation of An Air CushionDocument27 pagesStudy On Wave Calculation of An Air CushionEng Bagaragaza RomualdNo ratings yet
- Verruijt Consolidation 2008 EHSDocument18 pagesVerruijt Consolidation 2008 EHSNima DaneshNo ratings yet
- The Law of Rectilinear Diameter For The Liquid Gas Phase TransitionDocument3 pagesThe Law of Rectilinear Diameter For The Liquid Gas Phase Transitionagarwalashwin32No ratings yet
- Viscous Diss Tern in Energy EquationsDocument14 pagesViscous Diss Tern in Energy EquationsJohn Jonnalagadda100% (1)
- Ch2 Fluid Statics: - Fluid Either at Rest or Moving in ADocument24 pagesCh2 Fluid Statics: - Fluid Either at Rest or Moving in ARichard Periyanayagam100% (1)
- Gas Laws (Chem)Document27 pagesGas Laws (Chem)EncounteriGH100% (3)
- Chapter 3 Bernoulli Equation: 3.1 Flow Patterns: Streamlines, Pathlines, StreaklinesDocument24 pagesChapter 3 Bernoulli Equation: 3.1 Flow Patterns: Streamlines, Pathlines, StreaklinesManu KumarNo ratings yet
- ART Lou RVDocument8 pagesART Lou RVnicholas_j_vaughanNo ratings yet
- GATE 1991-2013 Topic Wise Solution PDFDocument89 pagesGATE 1991-2013 Topic Wise Solution PDFGanesh VishwanadhNo ratings yet
- A4........ ACoupled Vibration of A Cantilever Micro-Beam SubmergedDocument10 pagesA4........ ACoupled Vibration of A Cantilever Micro-Beam SubmergedyohannesNo ratings yet
- Annu Rev Fluid Mech - Bubble Dynamics and Cavitation - PlessetDocument42 pagesAnnu Rev Fluid Mech - Bubble Dynamics and Cavitation - PlessetKishor BorkarNo ratings yet
- Wave Propagation in Fluid LinesDocument23 pagesWave Propagation in Fluid Linesbaja2014No ratings yet
- The Dynamics of Cavitation BubblesDocument6 pagesThe Dynamics of Cavitation BubblesAlex DíazNo ratings yet
- Application of Cyclic Operation To Acetic-Water Separation Patrut 2019Document6 pagesApplication of Cyclic Operation To Acetic-Water Separation Patrut 2019nehaNo ratings yet
- .Jownal of Non - Newtonian Fluid Mechanics, 19 (1985) 229-234Document6 pages.Jownal of Non - Newtonian Fluid Mechanics, 19 (1985) 229-234Akin MuhammadNo ratings yet
- Surface Viscosity Vila1985Document8 pagesSurface Viscosity Vila1985mgra709No ratings yet
- Sinking of A Horizontal Cylinder: Dominic VellaDocument3 pagesSinking of A Horizontal Cylinder: Dominic VellaJuan Manuel ScarpettaNo ratings yet
- 2012 - T G Theofanous - The Physics of Aerobreakup. II. Viscous LiquidsDocument40 pages2012 - T G Theofanous - The Physics of Aerobreakup. II. Viscous LiquidsSurendra RatnuNo ratings yet
- Models - Cfd.boiling WaterDocument26 pagesModels - Cfd.boiling WaterShawonChowdhuryNo ratings yet
- FLUID MECHANICS - Module I (5 Files Merged)Document218 pagesFLUID MECHANICS - Module I (5 Files Merged)nithinvsNo ratings yet
- A Theory of TurbulenceDocument218 pagesA Theory of TurbulenceBhertrand GomesNo ratings yet
- C. W. PARK+G. M. HOMSY (1984) Two Phase Displacement in Hele Shaw Cells TheoryDocument18 pagesC. W. PARK+G. M. HOMSY (1984) Two Phase Displacement in Hele Shaw Cells TheoryLy HourNo ratings yet
- Consol Two-Tri1 DDocument9 pagesConsol Two-Tri1 DAbib TALLNo ratings yet
- Mini Project (Report) (Aditya Gunin)Document20 pagesMini Project (Report) (Aditya Gunin)Soham SahaNo ratings yet
- Static Liquid Holdup in Packed Beds of Spherical ParticlesDocument4 pagesStatic Liquid Holdup in Packed Beds of Spherical ParticlesaegosmithNo ratings yet
- Steam Z FactorDocument7 pagesSteam Z Factorralf.stein9265No ratings yet
- Ontents: Sample Problems Practice ProblemsDocument51 pagesOntents: Sample Problems Practice ProblemsBijimol BinuNo ratings yet
- On The Construction of Global Weak Solutions in The Kynch Theory of SedimentationDocument20 pagesOn The Construction of Global Weak Solutions in The Kynch Theory of SedimentationChristy Alexandra Solano GavelánNo ratings yet
- Mechanisms For Oscillations in Volume of Single Spherical Bubble Due To Sound Excitation in WaterDocument4 pagesMechanisms For Oscillations in Volume of Single Spherical Bubble Due To Sound Excitation in WaterAndres Camargo QuirogaNo ratings yet
- Physical Chemistry Establishes and Develops The: Pchem I 1.1Document26 pagesPhysical Chemistry Establishes and Develops The: Pchem I 1.1Kaaya GodfreyNo ratings yet
- Research On Solid-Liquid Coupling Dynamics of Pipe Conveying FluidDocument7 pagesResearch On Solid-Liquid Coupling Dynamics of Pipe Conveying FluidAdam StevensonNo ratings yet
- A Tomiyama - Terminal Velocity of Single Bubbles in Surface Tension Force Dominant RegimeDocument23 pagesA Tomiyama - Terminal Velocity of Single Bubbles in Surface Tension Force Dominant RegimeDiego NotlikethisNo ratings yet
- Keller MiksisDocument22 pagesKeller MiksisAjay SagarNo ratings yet
- Ajassp 2017 878 885Document8 pagesAjassp 2017 878 885vijayNo ratings yet
- General Information: 9.6 PP 100 / 20 PP 1.2Document3 pagesGeneral Information: 9.6 PP 100 / 20 PP 1.2vijayNo ratings yet
- Exalite-10 GB PDFDocument2 pagesExalite-10 GB PDFvijayNo ratings yet
- G CodeDocument1 pageG CodevijayNo ratings yet
- NGJKXCNG VFNGFGNDFGDocument1 pageNGJKXCNG VFNGFGNDFGvijayNo ratings yet
- Nsefo: Open - Mcxfo: Open - Ncdexfo: OpenDocument1 pageNsefo: Open - Mcxfo: Open - Ncdexfo: OpenvijayNo ratings yet
- Fundamentals of Momentum, Heat and Mass Transfer, 5 Edition Welty Et AlDocument10 pagesFundamentals of Momentum, Heat and Mass Transfer, 5 Edition Welty Et AlYangfan XuNo ratings yet
- 16B-Zero-Point Energy and Its EffectsDocument1 page16B-Zero-Point Energy and Its EffectsPramendra YadavNo ratings yet
- Dot Point CoreDocument70 pagesDot Point CoreShagun Varma100% (2)
- Mech (1) MC-studentDocument29 pagesMech (1) MC-studentanon-901414100% (3)
- PS2 Syllabus 2017 3Document3 pagesPS2 Syllabus 2017 3rayNo ratings yet
- Quantum Mechanics Lectures NoteDocument69 pagesQuantum Mechanics Lectures NoteNirmalya NandiNo ratings yet
- Course Mat.5 PDFDocument12 pagesCourse Mat.5 PDFAritra GhoshNo ratings yet
- PHYSICS SPM DICTIONARY@alinaimanaarif PDFDocument25 pagesPHYSICS SPM DICTIONARY@alinaimanaarif PDFAzrul AkmarNo ratings yet
- PROBLEMSDocument113 pagesPROBLEMSsmidggNo ratings yet
- Exam03 Sol f12Document12 pagesExam03 Sol f12hasib_07No ratings yet
- AQA GCSE Physics: Higher: Advance Information of Assessed Content 2022Document11 pagesAQA GCSE Physics: Higher: Advance Information of Assessed Content 2022Will ShuteNo ratings yet
- Simple Improvement of Momentum Interpolation Equation For Navier Stokes Equation Solver On Unstructured GridDocument6 pagesSimple Improvement of Momentum Interpolation Equation For Navier Stokes Equation Solver On Unstructured GridMuhammad IrfanNo ratings yet
- Solid-Liquid Mixing in Agitated Tanks Through Computational FluidDocument14 pagesSolid-Liquid Mixing in Agitated Tanks Through Computational FluidMANISHT PRATAP SINGHNo ratings yet
- Indepth Crash Investigation - Concept, Method, ProcedureDocument59 pagesIndepth Crash Investigation - Concept, Method, ProcedureArkan Hussein Al-rawhanyNo ratings yet
- 235808219question Bank Class XiDocument27 pages235808219question Bank Class XiAnonymous EImkf6RGdQNo ratings yet
- Tutorial Letter 101/3/2021: Classical MechanicsDocument11 pagesTutorial Letter 101/3/2021: Classical MechanicsDe JansenNo ratings yet
- Igcse Unit - C Forces Movement Shapeand MomentumDocument3 pagesIgcse Unit - C Forces Movement Shapeand Momentumapi-255623302No ratings yet
- Physics ECET by AANM VVRSR GVLDocument128 pagesPhysics ECET by AANM VVRSR GVLnandaNo ratings yet
- Practical Guide To The Use of Scalar EnergyDocument80 pagesPractical Guide To The Use of Scalar EnergyseraphimuseNo ratings yet
- Electrodynamics - USPDocument437 pagesElectrodynamics - USPLucas PereiraNo ratings yet
- IB Physics 2025 SyllabusDocument27 pagesIB Physics 2025 Syllabusmastering.alevels.physicsNo ratings yet
- Momentum PhET ActivityDocument2 pagesMomentum PhET ActivityZhiyu David ZouNo ratings yet
- PHYS4652 Assignment1Document2 pagesPHYS4652 Assignment1Yang Woo SeongNo ratings yet
- Questions On MomentumDocument2 pagesQuestions On MomentumSutharsini KangeyanNo ratings yet
- EEE Undergraduate 24-10-2011Document70 pagesEEE Undergraduate 24-10-2011Dzana AjanovicNo ratings yet
- Examples 2 MeasurementDocument43 pagesExamples 2 Measurementmoon starNo ratings yet
- Planar Jet Flow Through Rectangular NozzleDocument39 pagesPlanar Jet Flow Through Rectangular NozzleV S HARIKRISHNANo ratings yet
- SAT II Physics (SN)Document373 pagesSAT II Physics (SN)Ah BiNo ratings yet
- Correction FactorDocument20 pagesCorrection FactorAdwaith Gupta100% (2)
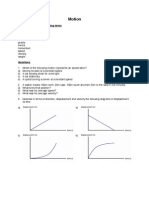
- Motion Revision Work SheetDocument4 pagesMotion Revision Work SheetabdulfcNo ratings yet