Professional Documents
Culture Documents
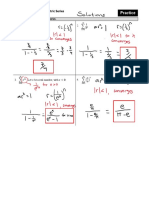
Sufficient
Uploaded by
Ajay Pratap SinghCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Sufficient
Uploaded by
Ajay Pratap SinghCopyright:
Available Formats
Notes on Sucient Conditions for Extrema
Francis J. Narcowich
Department of Mathematics
Texas A&M University
January 2006
1 The second variation
Let J[x] =
_
b
a
F(t, x, x)dt be a nonlinear functional, with x(a) = A and
x(b) = B xed. As usual, we will assume that F is as smooth as necessary.
The rst variation of J is
J
x
[h] =
_
b
a
_
F(t, x, x)
d
dt
F
x
_
h(t)dt,
where h(t) is assumed as smooth as necessary and in addition satises h(a) =
h(b) = 0. We will call such h admissible.
The idea behind nding the rst variation is to capture the linear part
of the J[x]. Specically, we have
J[x +h] = J[x] +J
x
[h] +o(),
where o() is a quantity that satises
lim
0
o()
= 0.
The second variation comes out of the quadratic approximation in ,
J[x +h] = J[x] +J
x
[h] +
1
2
2
J
x
[h] +o(
2
).
It follows that
2
J
x
[h] =
d
2
d
2
_
J[x +h]
_
=0
.
1
To calculate it, we note that
d
2
d
2
_
J[x +h]
_
=
_
b
a
2
_
F(t, x +h, x +
h)
_
dt.
Applying the chain rule to the integrand, we see that
2
_
F(t, x +h, x +
h)
_
=
_
F
x
h +F
x
h
_
= F
xx
h
2
+ 2F
x x
h
h +F
x x
h
2
,
where the various derivatives of F are evaluated at (t, x +h, x +
h). Set-
ting = 0 and inserting the result in our earlier expression for the second
variation, we obtain
2
J
x
[h] =
_
b
a
F
xx
h
2
+ 2F
x x
h
h +F
x x
h
2
dt .
Note that the middle term can be written as 2F
x x
h
h = F
x x
d
dt
h
2
. Using this
in the equation above, integrating by parts, and employing h(a) = h(b) = 0,
we arrive at
2
J
x
[h] =
_
b
a
_
_
F
xx
d
dt
F
x x
. .
Q
_
h
2
+ F
x x
..
P
h
2
_
dt
=
_
b
a
(P
h
2
+Qh
2
)dt. (1)
2 Legendres trick
Ultimately, we are interested in whether a given extremal for J is a weak
(relative) minimum or maximum. In the sequel we will always assume that
the function x(t) that we are working with is an extremal, so that x(t)
satises the Euler-Lagrange equation,
d
dt
F
x
= F
x
, makes the rst variation
J
x
[h] = 0 for all h, and xes the functions P = F
x x
and Q = F
xx
d
dt
F
x x
.
To be denite, we will always assume we are looking for conditions for the
extremum to be a weak minimum. The case of a maximum is similar.
Lets look at the integrand P
h
2
+ Qh
2
in (1). It is generally true that
a function can be bounded, but have a derivative that varies wildly. Our
intuition then says that P
h
2
is the dominant term, and this turns out to be
true. In looking for a minimum, we recall that it is necessary that
2
J
x
[h] 0
2
for all h. One can use this to show that, for a minimum, it is also necessary,
but not sucient, that P 0 on [a, b]. We will make the stronger assumption
that P > 0 on [a, b]. We also assume that P and Q are smooth.
Legendre had the idea to add a term to
2
J to make it nonnegative.
Specically, he added
d
dt
(wh
2
) to the integrand in (1). Note that
_
b
a
d
dt
(wh
2
)dt =
wh
2
|
b
a
= 0. Hence, we have this chain of equations,
2
J
x
[h] =
2
J
x
[h] +
_
b
a
d
dt
(wh
2
)dt
=
_
b
a
(P
h
2
+Qh
2
+
d
dt
(wh
2
))dt
=
_
b
a
_
P
h
2
+ 2wh
h + ( w +Q)h
2
_
dt (2)
=
_
b
a
P
_
h +
w
P
h
_
2
dt +
_
b
a
_
w +Q
w
2
P
_
h
2
, (3)
where we completed the square to get the last equation. If we can nd w(t)
such that
w +Q
w
2
P
= 0, (4)
then the second variation becomes
2
J
x
[h] =
_
b
a
P
_
h +
w
P
h
_
2
dt. (5)
Equation (4) is called a Riccati equation. It can be turned into the
second order linear ODE below via the substitution w = ( u/u)P:
d
dt
_
P
du
dt
_
+Qu = 0, (6)
which is called the Jacobi equation for J. Two points t = and t = , =
, are said to be conjugate points for Jacobis equation if there is a solution
u to (6) such that u 0 between and , and such that u() = u( ) = 0.
When there are no points conjugate to t = a in the interval [a, b], we can
construct a solution to (6) that is strictly positive on [a, b]. Start with the
two linearly indepemdent solutions u
0
and u
1
to (6) that satsify the initial
conditions
u
0
(a) = 0, u
0
(a) = 1, u
1
(a) = 0, and u
1
(a) = 1.
3
Since there is no point in [a, b] conjugate a, u
0
(t) = 0 for any a < t b.
In particular, since u
0
(a) = 1 > 0, u(t) will be strictly positive on (a, b].
Next, because u
1
(a) = 1, there exists t = c, a < c b, such that u
1
(t)
1/2 on [a, c]. Moreover, the continuity of u
0
and u
1
on [c, b] implies that
min
ctb
u
0
(t) = m
0
> 0 and min
ctb
u
1
(t) = m
1
R. It is easy to check
that on [a, b],
u :=
1 + 2|m
1
|
2m
0
u
0
+u
1
1/2,
and, of course, u solves (6).
This means that the substitutuion w = ( u/u)P yields a solution to the
Riccati equation (4), and so the second variation has the form given in (5).
It follows that
2
J
x
[h] 0 for any admissible h. Can the second variation
vanish for some h that is nonzero? That is, can we nd an admissible h 0
such that
2
J
x
[h] = 0? If it did vanish, we would have to have
P
_
h +
w
P
h
_
2
= 0, a t b,
and, since P > 0, this implies that
h +
w
P
h = 0. This rst order linear
equation has the unique solution,
h(t) = h(a)e
t
a
w()
P()
d
.
However, since h is admissible, h(a) = h(b) = 0, and so h(t) 0. We have
proved the following result.
Proposition 2.1. If there are no points in [a, b] conjugate to t = a, the
the second variation is a positive denite quadratic functional. That is,
2
J
x
[h] > 0 for any admissible h not identically 0.
3 Conjugate points
There is direct connection between conjugate points and extremals. Let
x(t, ) be a family of extremals for the functional J depending smoothly on
a parameter . We will assume that x(a, ) = A, which will be independent
of . These extremals all satisfy the Euler-Lagrange equation
F
x
(t, x(t, ), x(t, ) =
d
dt
F
x
(t, x(t, ), x(t, ).
4
If we dierentiate this equation with respect to , being careful to correctly
apply the chain rule, we obtain
F
xx
x
+F
x x
x
=
d
dt
_
F
x x
x
+F
x x
x
_
=
dF
x x
dt
x
+F
x x
x
+
d
dt
_
F
x x
x
_
.
Cancelling and rearranging terms, we obtain
_
F
xx
d
dt
F
x x
_
x
d
dt
_
F
x x
x
_
= 0. (7)
Set = 0 and let u(t) =
x
(t, 0). Observe that the functions in the equation
above, which is called the variational equation, are just P = F
x x
and Q =
F
xx
d
dt
F
x x
. Consequently, (7) is simply the Jacobi equation (6). The
dierence here is that we always have the initial conditions,
_
_
u(a) =
x
(a, 0) =
A
= 0,
u(a) =
x
(a, 0) = 0.
We remark that if u(a) = 0, then u(t) 0.
What do conjugate points mean in this context? Suppose that t = a is
conjugate to t = a. Then we have
x
( a, 0) = u( a) = 0,
which holds independently of how our smooth family of extremals was con-
structed. It follows that at t = a, we have x( a, ) = x( a, 0) + o(). Thus,
the family either crosses again at a, or comes close to it, accumulating to
order higher than there.
4 Sucient conditions
A sucient condition for an extremal to be a relative minimum is that the
second variation be strongly positive denite. This means that there is a
c > 0, which is independent of h, such that for all admissible h one has
2
J
x
[h] ch
2
H
1
,
5
where H
1
= H
1
[a, b] denotes the usual Sobolev space of functions with
distributional derivatives in L
2
[a, b].
Let us return to equation (2), where we added in terms depending on
an arbitrary function w. In the integrand there, we will add and subtract
P
h
2
, where is an arbitary constant. The only requirement for now is
that 0 < < min
t[a,b]
P(t). The result is
2
J
x
[h] =
_
b
a
_
(P )
h
2
+ 2wh
h + ( w +Q)h
2
_
dt +
_
b
a
h
2
dt .
For the rst integral in the term on the right above, we repeat the argument
that was used to arrive at (5). Everything is the same, except that P is
replaced by P . We arrive at this:
2
J
x
[h] =
_
b
a
(P )
_
h +
w
P
h
_
2
dt
+
_
b
a
_
w +Q
w
2
P
_
h
2
+
_
b
a
h
2
dt .
(8)
We continue as we did in section 2. In the end, we arrive at the new
Jacobi equation,
d
dt
_
(P )
du
dt
_
+Qu = 0 . (9)
The point is that if for the Jacobi equation (6) there are no points in [a, b]
conjugate to a, then, because the solutions are continuous functions of the
parameter , we may choose small enough so that for (9) there will be no
points conjugate to a in [a, b]. Once we have fouund small enough for this
to be true, we x it. We then solve the corresponding Riccati equation and
employ it in (8) to obtain
2
J
x
[h] =
_
b
a
(P )
_
h +
w
P
h
_
2
dt +
_
b
a
h
2
dt
_
b
a
h
2
dt .
Now, for an admissble h, it is easy to show that
_
b
a
h
2
dt
(ba)
2
2
_
b
a
h
2
dt, so
that we have
h
2
H
1
=
_
b
a
h
2
dt +
_
b
a
h
2
dt
_
1 +
(b a)
2
2
__
b
a
h
2
dt.
6
Consequently, we obtain this inequality:
2
J
x
[h]
1 +
(ba)
2
2
h
2
H
1
= ch
2
H
1
,
which is what we needed for a relative minimum. We summarize what we
found below.
Theorem 4.1. A sucient condition for an extremal x(t) to be a relative
minimum for the functional J[x] =
_
b
a
F(t, x, x)dt, where x(a) = A and
x(b) = B, is that P(t) = F
x x
(t, x, x) > 0 for t [a, b] and that the interval
[a, b] contain no points conjugate to t = a.
7
You might also like
- Lecture - 20: 1 Beta DistributionDocument4 pagesLecture - 20: 1 Beta DistributionAjay Pratap SinghNo ratings yet
- CCCP Civil FL 2015december18Document6 pagesCCCP Civil FL 2015december18Ajay Pratap SinghNo ratings yet
- Paper 3066 PDFDocument15 pagesPaper 3066 PDFAjay Pratap SinghNo ratings yet
- Hindi MoviesDocument38 pagesHindi MoviesAjay Pratap SinghNo ratings yet
- Part 1: Getting Started: CSE342 - Lab 4: Packet Sniffing With WiresharkDocument16 pagesPart 1: Getting Started: CSE342 - Lab 4: Packet Sniffing With WiresharkAjay Pratap SinghNo ratings yet
- MA 473 Computational Finance Lab 5: Rahul Agrawal 10012326Document2 pagesMA 473 Computational Finance Lab 5: Rahul Agrawal 10012326Ajay Pratap SinghNo ratings yet
- Indian Institute of Technology Guwahati: I (D) Q TFR 1011 1I1Document1 pageIndian Institute of Technology Guwahati: I (D) Q TFR 1011 1I1Ajay Pratap SinghNo ratings yet
- Back To MDE: 28 February and 1 March 2013Document31 pagesBack To MDE: 28 February and 1 March 2013Ajay Pratap SinghNo ratings yet
- Age of ImperialismDocument30 pagesAge of ImperialismAjay Pratap Singh100% (1)
- Transforation Around GlobeDocument24 pagesTransforation Around GlobeAjay Pratap Singh100% (1)
- Industrila RevolutionDocument26 pagesIndustrila RevolutionAjay Pratap SinghNo ratings yet
- Grest War - 1 World WarDocument26 pagesGrest War - 1 World WarAjay Pratap Singh100% (1)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (400)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- RPT MATH DLP YEAR 6 2023-2024 by Rozayus AcademyDocument13 pagesRPT MATH DLP YEAR 6 2023-2024 by Rozayus AcademyROSMALIZA BINTI ABDUL LATIB MoeNo ratings yet
- Oakdale Middle School 8th Grade Math SyllabusDocument4 pagesOakdale Middle School 8th Grade Math Syllabustree5215No ratings yet
- Option B Shahine PorterDocument4 pagesOption B Shahine PortershahineNo ratings yet
- 5-Multiple Integrals and Their Applications PDFDocument63 pages5-Multiple Integrals and Their Applications PDFLoo Javier Mamani Quea100% (1)
- EM220 Bachelor of Engineering (Hons) Mechanical MEC 500 Numerical Method With Application Assignment Emd6M8ADocument7 pagesEM220 Bachelor of Engineering (Hons) Mechanical MEC 500 Numerical Method With Application Assignment Emd6M8A000No ratings yet
- Numeracy Level Assessment Inventory (Pre-Test/ Grade Five) : ScoreDocument15 pagesNumeracy Level Assessment Inventory (Pre-Test/ Grade Five) : ScoreRemalyn BurgosNo ratings yet
- Q No. 1 Bisection Method MATLAB Code: - : Short All AllDocument29 pagesQ No. 1 Bisection Method MATLAB Code: - : Short All AllEngrSalman khanNo ratings yet
- Project Euler ProblemsDocument214 pagesProject Euler Problemspeter100% (1)
- Lesson 1.1 - FACTORING POLYNOMIAL WITH GREATEST COMMON MONOMIAL FACTOR, DIFFERENCE OF TWO SQUARE AND SUM AND DIFFERENCE OF TWO CUBESDocument31 pagesLesson 1.1 - FACTORING POLYNOMIAL WITH GREATEST COMMON MONOMIAL FACTOR, DIFFERENCE OF TWO SQUARE AND SUM AND DIFFERENCE OF TWO CUBESAnnalyn Ortiz CoruñaNo ratings yet
- CL09 WS Coordinate Geometry SHAROL 2023-24Document5 pagesCL09 WS Coordinate Geometry SHAROL 2023-24JOEL SUNNYNo ratings yet
- Example RT#001 Recruitment Test - Maths and Logic: (Print Your Name)Document5 pagesExample RT#001 Recruitment Test - Maths and Logic: (Print Your Name)muussaNo ratings yet
- 10.2 Working With Geometric Series: PracticeDocument4 pages10.2 Working With Geometric Series: Practice张书No ratings yet
- Summative Test in Special ProductsDocument3 pagesSummative Test in Special ProductsNeil JoNo ratings yet
- Eular Method TheoryDocument5 pagesEular Method Theory064 Jayapratha P RNo ratings yet
- Logic Gates Boolean Algebra: Instructor: Afroza SultanaDocument44 pagesLogic Gates Boolean Algebra: Instructor: Afroza SultanaSamina Tohfa100% (1)
- Integration Partial Fractions PDFDocument10 pagesIntegration Partial Fractions PDFrendie100% (1)
- CPP: Parabola: X Y Ax A at at B at at Acab T T Y AxDocument3 pagesCPP: Parabola: X Y Ax A at at B at at Acab T T Y AxSamridh GuptaNo ratings yet
- Fundamentals of Data Structures - Ellis Horowitz, Sartaj SahniEllDocument542 pagesFundamentals of Data Structures - Ellis Horowitz, Sartaj SahniElljely thakkarNo ratings yet
- ASM - Abstract StateMachines Theory and Applications (Lecture Notes in Computer Science) PDFDocument390 pagesASM - Abstract StateMachines Theory and Applications (Lecture Notes in Computer Science) PDFyorwuin100% (1)
- A New Look at An Old EquationDocument463 pagesA New Look at An Old Equationslipstream311 -113No ratings yet
- Certc - Davao Diagnostic Exam: Instruction: Select The Correct Answer For Each of The FollowingDocument4 pagesCertc - Davao Diagnostic Exam: Instruction: Select The Correct Answer For Each of The FollowingJj JumawanNo ratings yet
- Math Grade 1 Curriculum Map 2014-15.HighlandCentralSchoolDistrictDocument11 pagesMath Grade 1 Curriculum Map 2014-15.HighlandCentralSchoolDistrictAdame JericNo ratings yet
- Art Unit Plan Exploring Shapes in ArtDocument13 pagesArt Unit Plan Exploring Shapes in Artapi-265643246No ratings yet
- NMTC 2022 Prelims Sub Junior Paper SolutionDocument15 pagesNMTC 2022 Prelims Sub Junior Paper SolutionDavis JhonnyNo ratings yet
- Branch Name B.E. Computer Science and Engineering: Semes Ter Subject Name Subject Code Exam Date SessionDocument3 pagesBranch Name B.E. Computer Science and Engineering: Semes Ter Subject Name Subject Code Exam Date SessionDinesh DineshNo ratings yet
- Mathematical Olympiad 2018Document6 pagesMathematical Olympiad 2018Saksham100% (1)
- 519H0206 Homework3Document12 pages519H0206 Homework3King NopeNo ratings yet
- Calculus Integration RulesDocument2 pagesCalculus Integration RulesAladdin PrinceNo ratings yet
- Tensor Programs VDocument48 pagesTensor Programs ValekthieryNo ratings yet
- 1815 13 PDFDocument24 pages1815 13 PDFsiamak001No ratings yet