Page 1 of 2

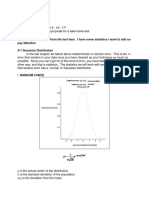
Appendix B: Measuring Skew

Scientists who use statistics often assume that a set of data is normally distributed, but is this assumption ever violated, and how can you
tell? That is, how can you tell whether a distribution of scores is normally distributed, or skewed? Indeed, it is good to know whether there is
large and significant skew to your distribution; if so, a transformation of the data to normalize the data may be necessary. This is so,
because nearly all inferential statistical tests assume that the data is normally distributed; hence, violations of normality can lead to serious
problems when interpreting data.
All formulae that have been proposed to measure skew are based on the assumption that the difference between the mean and the mode
will be zero if the distribution is normal. Early measures of skew subtracted the mode (Mo) from the mean and then standardize that
difference by dividing the difference by the standard deviation of the distribution:

If the mean is less than the mode the resulting value will be negative and the distribution is negatively skewed. If the mean is greater than
the mode the resulting value will be positive and the distribution is positively skewed.
The common formula for measuring skew, which is the third moment around a mean, is:

You must use the estimated standard deviation, because you need to determine if the skew is significant.
Say the following set of n = 8 scores are collected and the skew must be determined. The table lists all of steps necessary for calculating
the skew:

X
9

3.5

12.25

1.464

3.140

3.5

12.25

1.464

3.140

0.5

0.25

.209

0.009

-0.5

0.25

-.209

-0.009

-0.5

0.25

-.209

-0.009

-1.5

2.25

-.628

-0.248

-2.5

6.25

-1.046

-1.144

-2.5

6.25

-1.046

-1.144

X = 44

The estimated standard deviation is:

https://sites.google.com/site/fundamentalstatistics/appendix-b?tmpl=%2Fsystem%2Fapp%... 11/4/2012

Page 2 of 2

Solving for the skew, we have:

This value is positive, which indicates that the distribution is positively skewed. The range of this measure of skew is between only -1.00
and +1.00; hence, it is easily used to determine the magnitude of any skew. Any value greater than 0.3 is considered severe skew; thus,
in the example above, the skew of 0.710 indicates a severely positively skewed distribution. But this value provides only a measure of the
distributions skew. It would be better to know if the skew of the distribution is so large that it deviates significantly from what is expected in
the population, which is no skew. To determine whether the skew of the distribution is significant, you first calculate the estimated standard
error of skew, which is estimated in the following equation:

From this example, the estimated standard error of skew is:

The statistical significance test for distribution skew is a type of z-score:

Thus, in this example, the z-score of skew is:

To determine whether the skew is statistically significant, locate that z-score in the z-Tables. Look at the probability of obtaining that z-score
in one tail (Column 3). If the probability is .05 or less, then the skew is statistically significant. You always use a one-tail test rather than a
two-tail test, because skew can go in one direction (one tail) only. Also, note that the magnitude of the estimated standard error of skew will
decrease as n increases, making it more likely that you will find significant skew with larger sample size. In effect, having larger sample
sizes actually punishes you, which is counterintuitive, because larger sample sizes are supposed to better approximate the population.
However, in the case of skew, it is assumed that larger sample sizes will create better approximates toward a normal distribution; that is, as
the sample size increases, the skew should decrease. If this is the case, then as the sample size increases and the estimated standard
error of skew decreases, so too should the magnitude of skew. The result will be less likelihood of finding significant skew.

https://sites.google.com/site/fundamentalstatistics/appendix-b?tmpl=%2Fsystem%2Fapp%... 11/4/2012