Professional Documents
Culture Documents
B-E Condensation PDF
Uploaded by
krish_cvr2937Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
B-E Condensation PDF
Uploaded by
krish_cvr2937Copyright:
Available Formats
Rajaram Nityananda
Bose-Einstein Condensation
Birds of a Feather Flock Together
R Nityananda
Rajaram Nityananda
works at the Raman
Research Institute,
Bangalore, mainly on
areas of condensed matter
physics and astronomy
accessible via optics and
statistical physics. He
continues to teach and
popularise rather basic
areas of physics while
admiring more modem
trends from a safe
distance. His tastes in
travel, music, and food
are optimally satisfied by
listening to Hindi fllm
music half as old as he is
while eating potato chips
in a sleeper coach.
142
In 1924 Bose introduced a counting nale for the states of a
gas of photons which explained Planck's law for thermal
radiation at one stroke. Einstein not only recognised the
importance ofthis idea but immediately applied it to a more
conventional gas like helium. In this case, unlike that of
radiation, the number of particles is held fixed. He derived
the stunning conclusion that a finite fraction of the particles could settle in the lowest energy state even above
absolute zero. These ideas had to wait fourteen years for
their first application. Seventy years later they are being
used in atomic physics laboratories all over the world.
Everybody is talking about Bose-Einstein condensation. This
discovery made in 1924 seems to have exploded like a time bomb
seventy years later. How did these two names come together?
S N Bose was a teacher of physics in Dacca, as far from the
mainstream as one could imagine. Einstein was, of course, the
giant who had already given the world special and general
relativity, the light quantum, Brownian motion. The story is an
extraordinary one, and it has been told earlier in these pages
when the central figure was Bose [1]. Now let us look at it from
Einstein's point of view. He struggled for 20 years with the
concept of the light quantum and Planck's radiation formula
[2]. Suddenly, a bolt from the blue arrived. Someone he had
never heard of was proposing a new derivation of Planck's
formula for the intensity of blackbody radiation. It made no
reference to waves whatsoever, being stated entirely in the
language of photons. Many times in the history of mathematics
and physics, such letters have been ignored. The idea is too
revolutionary and the author too unknown. Let us salute Einstein
for not taking that easy path. He read the paper, recognised its
Appea cod in Vol. 5, No.4, pp .46,51, 2000 -vV\fIfvv------R-E-S-O-N-A-N-C-E-1-D-e-ce-m-b-e-r-Z-o-o-s
~,
Bose-Einstein Condensation
";<:{~~.,
'-ii
deep originality, translated it into German, wrote a covering
note on its importance and forwarded it for publication.
Superficially, the mathematical steps in Bose's discussion of a
gas of photons resembled what Boltzmann had gone through
fifty years earlier, in the discussion of ordinary gases. We
describe the basic idea here. Common observation shows that a
gas fills its container uniformly. In other words, the probability
distribution of the position of any particle in the gas is a constant
function within the container. A more difficult experiment is
needed if we want to find the probability distribution of the xcomponent of the velocity of the molecules (for example). This
is found to be the famous bell shaped curve known as the
Gaussian distribution. As a function of velocity it is e(-const x v2x )
and similarly for they andz components. In terms of the energy
E of a state, this translates into a number of particles per state, n
proportional to e (-fJE). The science of statistical physics tries to
understand why these particular distributions, for the position
and for the velocity, are special. After all, nothing in the laws of
physics prevents all the molecules being on one side of the
container, at least for some time. Likewise, nothing forbids a
situation where all the molecules have the same speed, half
going to the left and half to the right. Again, this situation could
occur at some time and change because of collisions.
Boltzmann took two approaches to the problem, both of them
deep and fruitful. One was to ask how any such initial state
would evolve with time. Clearly, not even Boltzmann could say
with certainty what the precise outcome of a huge number of
molecular collisions would be. So he made a guess about what
was the most probable number of collisions changing the velocities of the molecules in various ways. This led to the famous
distribution law named after him and is sketched in Figure 1.
The probability of finding a molecule in a single state of a given
energy is proportional to an exponential function of the energy.
But this method of collisions is not the whole story. One can and Boltzmann did -look at the matter in a different way. Take
a coin tossed ten times. To say that five heads turned up is not a
-RE-S-O-N-A-N-C-E--I--D-ec-e-m-b-e-r-2-0-05----------~-----------------------------143-
Rajaram Nityananda
Figure 1. The Boltzmann
distribution of particles
over energy states.
low temperature
\/
, :
, '", -"~.
".,'.
'\
intecmediate tempetature
.~............
Eneqy of the state E
lThis can occur in 252 ways out
of a total 1024 possible outcomes of ten tosses.
complete description, because we are not saying which of the
tosses were heads, this can happen in manyl ways. Similarly, to
say that a gas has a certain distribution of velocities is not a
complete description; this can happen in many ways. All one has
to do is to count the number of ways, and this tells us the state in
which the gas is most likely to be found. Boltzmann was able to
show that the most probable behaviour of a gas, the one which
can occur in the largest number of ways, is to fill the container
uniformly, and have a gaussian distribution for each component
of the velocity vector.
With this background, we can state what was revolutionary in
the paper that Bose sent to Einstein. Treating the photons as a
gas, he used a counting rule different from Boltzmann's. Again,
we give only the basic idea here. Take two different boxes, called
I and 2, and two balls, called A and B. Let us look at all possible
states of the system. Clearly there are four of them, which we can
symbolically denote as Al BI, A2 B2, Al B2 and A2 Bl. Bose's
counting rule was equivalent to saying there were only three
states, with the last two viz. AIB2 and A2Bl, counted as one.
This was as if someone had rubbed off the letters A and B
painted on the two balls. One says that in Bose's way of counting,
the particles are indistinguishable. We can see what effect this has
in our simple example. The two cases in which both the particles
-44------------------------------~----------R-E-SO-N-A-N-C-E--I--D-e-ce-m-b-e-r-2-0-0-5
Bose-Einstein Condensation
~~t,'<,
"---"'
Figure 2. The BoseEinstein distribution for a
gas at a high and at a low
temperature.
~'"
Peak at zero enelBY
at low temperatures
'~
~
...............
high tempecatures
~above the condensation
.... .... ....
.......
tempecature
Enecgy of the state E
are in the same state (A 1 Bland A2 B2) now get two thirds of the
weight, instead of half as in Boltzmann's way of counting. This
result carries over in more general cases with many more boxes
and balls. The example given above shows that the Bose distribution 2 gives more weightage to situations in which many
particles occupy the same state. And this extra weightage was
able to explain the observed distribution of photons over frequency in thermal radiation.
Einstein had an immediate additional deep insight into the
consequences of Bose's counting rule. In the case of photons, the
total number of particles actually decreases as we decrease the
total energy of the system (equivalently, as we lower the temperature). In fact, the total number of photons is proportional to
the cube of the absolute temperature. Since their average energy
is proportional to the temperature, the total energy per unit
volume is proportional to the fourth power of the temperature.
However, if we apply Bose statistics to a gas of helium atoms in
a box, we must obviously keep the number of atoms fixed as the
temperature varies. So the precise formula for the number of
atoms in a state with energy E is different from what Bose used
in the case of photons. It looks very similar, but contains an
additional term denoted by J.l subtracted from the energy. The
formula reads 3
n = 1/(1 +exp(ft.-E-p))).
2 The
new distribution law reads
HI. P is inversely
proportional to the temperature
n=lI(exp(pE
p= 11ks T with ks=Boltzmann's
constant.
3 One simple way of understanding the origin of such a term is as
follows. let us imagine a "reservoir" which contains a large number of helium atoms, all having
energy p. Connect the reservoir
to our box. Every time we move a
particle from the reservoir into
our box to a state of energy E. the
total energy of the system
changes by E-p. The box alone
now behaves like a system with
a variable number of particles.
where the energy E is replaced
by E-p. Clearly p. cannot be
greater than zero in this formula
since n would become negative
for E< p.
-R-ES-O-N-A-N--CE--I--D-e-c-e-m-b-e-r-2-0-0-5----------~-------------------------------145-
Rajararn Nityananda
This simple extra term has profound consequences. As the
temperature is lowered, more and more particles pile into the
lowest energy state. (For the gas of photons, they just disappear
from the system). At a low temperature, but one which is still above
absolute zero, the answer for the number of particles in the lowest
state becomes infinite because f.J approaches zero from below. A
lesser man might have concluded that something absurd was
happening and the whole counting rule had to be abandoned.
But Einstein realised that this infinite answer, though wrong,
held the key to what was really happening in the gas as it was
being cooled. He boldly said that one has to treat the lowest
energy state as a separate entity from all the other states. All
physical quantities would receive separate contributions from
the lowest state, called the 'condensate', and from all other
states. In a Boltzmann gas the contribution of any single state,
even the one of lowest energy, is negligible because there are so
many states which have nearby energies. But the Bose counting
rule tilts the balance in favour of a finite fraction of the particles
being in the lowest energy state, below the special value of the
temperature which Einstein had calculated. The values of density N and temperature T can be described as those which give
approximately one particle per thermal de Broglie wavelength
AT' For typical energy kBT, the corresponding momentum is
(2mkBT )112 and the wavelength A,. equals h/(2mk BT) 112. The
number of particles in a volume A,3 T is N(h 3/(2mk BT)3/2). When
this exceeds 14.54, the condensation begins. This can be achieved
by raising N or lowering T.
One should remember that Einstein was not motivated by any
experimental fact regarding gases in his work. He was following
the basic principles of statistical physics to their logical, though
amazing, conclusion. He also had a deep conviction that Bose's
counting rule was not just a trick to undentand radiation but a
new general principle. When Einstein wrote his paper, and for
more than a decade later, it did not appear that there was any
direct connection with known phenomena. Even fourteen years
later, in 1938, the eminent quantum and statistical physicist
-46-----------------------------~----------R-ES-O-N-A-N-C-E--1--oe-c-e-m-be-r--20-0-S
Bose-Einstein Condensation
Fritz London could say that "In the course of time, the degeneracy of the Bose-Einstein gas has rather got the reputation of
having a purely imaginary existence". In the same paper that we
have quoted, London noted that at the density of liquid helium,
the temperature for Bose-Einstein condensation of an ideal gas
would be about three degrees above absolute zero.4 Liquid
helium shows new properties below 2.1 degrees Kelvin [3].
London boldly suggested that these new properties were a
consequence of Bose-Einstein condensation. He was fully aware
that liquid helium was very far from being an ideal gas. There is
a strong repulsive force between two atoms which came too close
to each other, and a weaker attractive force at larger distances.
Recent experiments, sixty years after London, show that his
guess regarding liquid helium was right. About ten per cent of
the atoms have zero momentum at absolute zero. (In an ideal gas
this would have been 100%.)
This subject took another tum in 1995, when experimenters in
the US were able to produce a Bose-Einstein condensate for
Rubidium atoms. In this case, the density was low enough that
Einstein's original ideas, with small modifications, could be
applied [4]. This is now a very active field of experimental
physics. Nowadays, a beam of atoms in the same quantum state
is called an 'atom laser' and various ingenious schemes for producing and utilising such beams are being invented. This is
expected to give rise to extremely accurate measurements of
time and other physical quantities.
Statistical physics was certainly Einstein's early love. He had
written papers on the statistical basis of thermodynamics even
before his relativity papers - unfortunately, they mainly rediscovered what Gibbs had already just done. His discussions of
Brownian motion, of photons, of critical opalescence, are all
gems of statistical thinking. And his single paper on condensation in a gas obeying Bose statistics should be counted amongst
these gems. Anyone else who did just this work would have
acquired a towering reputation. But Einstein the statistical
physicist was ultimately eclipsed by Einstein the relativist.
~$~<'
.........
We should add that not all kinds
of identical particles obey Bose
statistiCS and show condensation. Electrons, for example, show
Fermi statistics and behave in a
completely different way at low
temperatures. The same is true
of 3He, the rarer isotope of he-
lium!
Suggested Reading
[1] Resonance, VoI.l,No.2,p.92,
1996.
[2] N Mukunda, Resonance,
Vol.S, No.3, p.3S, 2000.
[3] R Srinivasan, Resonance,
Vo1.2, No.2, p.S, 1997.
[4] Rajaram Nityananda, Reso
nance, VoI.l, No.2, p.l11,
1996.
Address for Correspondence
R Nityananda
Raman Research Institute
Sadashivanagar
Bangalore 560 080, India.
-RE-S-O-N-A-N-C-E--I--D-e-Ce-m-be--r--200--5----------~-------------------------------14-7
You might also like
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- SP401-404 IV Sem Model PaperDocument8 pagesSP401-404 IV Sem Model Paperkrish_cvr2937No ratings yet
- Set Kerala 2008Document15 pagesSet Kerala 2008krish_cvr2937No ratings yet
- Production of Sound: - : Demo WatermarkDocument8 pagesProduction of Sound: - : Demo Watermarkkrish_cvr2937No ratings yet
- 34556-11820-JEST Sample Question PhysicsDocument1 page34556-11820-JEST Sample Question PhysicsTrisha BanerjeeNo ratings yet
- Physics Doubts: Best Answer: The Angle of Deviation, by Which The Light of A Particular Wavelength Gets Deviated OnDocument1 pagePhysics Doubts: Best Answer: The Angle of Deviation, by Which The Light of A Particular Wavelength Gets Deviated Onkrish_cvr2937No ratings yet
- Work, Power& EnergyDocument11 pagesWork, Power& Energykrish_cvr2937No ratings yet
- Maxwell's Equations Describe How Electric Charges and Electric Currents Create Electric and MagneticDocument1 pageMaxwell's Equations Describe How Electric Charges and Electric Currents Create Electric and Magnetickrish_cvr2937No ratings yet
- How Do ATMs WorkDocument1 pageHow Do ATMs Workkrish_cvr2937No ratings yet
- EP II Aug18Document2 pagesEP II Aug18krish_cvr2937No ratings yet
- Physics As An Important Part of EngineeringDocument1 pagePhysics As An Important Part of Engineeringkrish_cvr2937No ratings yet
- Candle ScienceDocument5 pagesCandle Sciencekrish_cvr2937No ratings yet
- AIEEE Paper PhysicsDocument16 pagesAIEEE Paper Physicskrish_cvr2937No ratings yet
- Conversion Factors of Magnetic Measurements: Si To CgsDocument6 pagesConversion Factors of Magnetic Measurements: Si To Cgskrish_cvr2937No ratings yet
- Goodfood PDFDocument29 pagesGoodfood PDFkrish_cvr2937No ratings yet
- David Copperfield PDFDocument1,307 pagesDavid Copperfield PDFPopescu LauraNo ratings yet
- How Black Holes WorkDocument2 pagesHow Black Holes Workkrish_cvr2937No ratings yet
- How Did The Internet StartDocument3 pagesHow Did The Internet Startkrish_cvr2937No ratings yet
- June 2016Document1 pageJune 2016krish_cvr2937No ratings yet
- How Light Emitting Diodes WorkDocument2 pagesHow Light Emitting Diodes Workkrish_cvr2937No ratings yet
- I Year B. Tech Course File Contents: ACE Engineering CollegeDocument1 pageI Year B. Tech Course File Contents: ACE Engineering Collegekrish_cvr2937No ratings yet
- Black HolesDocument6 pagesBlack Holeskrish_cvr2937No ratings yet
- How Computer Viruses WorkDocument2 pagesHow Computer Viruses Workkrish_cvr2937No ratings yet
- EP II Apr18Document2 pagesEP II Apr18krish_cvr2937No ratings yet
- The Design of A Nuclear ReactorDocument14 pagesThe Design of A Nuclear Reactorkrish_cvr2937No ratings yet
- Bohr&atomic Structure PDFDocument8 pagesBohr&atomic Structure PDFkrish_cvr2937No ratings yet
- The Royal Family Copper Silver Gold ReferencesDocument10 pagesThe Royal Family Copper Silver Gold Referenceskrish_cvr2937No ratings yet
- 10-Tips-For Will PowerDocument2 pages10-Tips-For Will Powerkrish_cvr2937No ratings yet
- Applications of Crystal DefectsDocument2 pagesApplications of Crystal Defectskrish_cvr2937No ratings yet
- How Black Holes WorkDocument3 pagesHow Black Holes Workkrish_cvr2937No ratings yet
- Eddy CurrentDocument9 pagesEddy Currentkrish_cvr2937No ratings yet
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (400)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Electrochemistry Short Answers Type Questions PDFDocument7 pagesElectrochemistry Short Answers Type Questions PDFAKSHAT KUMARNo ratings yet
- Chapter 5 - Chemical BondingDocument6 pagesChapter 5 - Chemical BondingSudhan NairNo ratings yet
- Biochemistry PPT Part-2Document66 pagesBiochemistry PPT Part-2Gajendra Singh RaghavNo ratings yet
- Chapter 4 Ionic EquilibriumDocument61 pagesChapter 4 Ionic EquilibriumSuraj BhattaraiNo ratings yet
- 5-Black Oil SimulationDocument84 pages5-Black Oil SimulationAssholeNo ratings yet
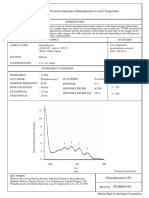
- Phosphorescence Excitation Spectrum of Benzophenone at Liq.N TemperatureDocument5 pagesPhosphorescence Excitation Spectrum of Benzophenone at Liq.N TemperatureNisar Ali Mphil-Chem ANo ratings yet
- Boyles Law and Charles LawDocument7 pagesBoyles Law and Charles Lawᜃᜒᜋ᜔ ᜊᜒᜎ᜔ᜌᜈ᜔ᜆᜒNo ratings yet
- Styrene Butadiene RubberDocument9 pagesStyrene Butadiene Rubberdashali1100% (1)
- Engro's Experience With Implementation of A S-300 Converter During A Normal T/ADocument10 pagesEngro's Experience With Implementation of A S-300 Converter During A Normal T/Avaratharajan g rNo ratings yet
- Chapter Eight Semiconductor Crystals: ElementsDocument50 pagesChapter Eight Semiconductor Crystals: ElementsKhanh Nguyen HuuNo ratings yet
- 1 Chemistry Module Chapter 1 Introduction To ChemistryDocument20 pages1 Chemistry Module Chapter 1 Introduction To ChemistryBj OcsenaNo ratings yet
- Drafting Mechanical Layout and DetailsDocument60 pagesDrafting Mechanical Layout and Detailsrannie joy glor100% (1)
- Test-07 PaperDocument13 pagesTest-07 PaperAashika DhareNo ratings yet
- Ec PH Manual 06 09 2016Document20 pagesEc PH Manual 06 09 2016YoussefNo ratings yet
- Natural Waxes: Candelilla Wax CG-4 Candelilla Wax CG-7Document3 pagesNatural Waxes: Candelilla Wax CG-4 Candelilla Wax CG-7email kantorNo ratings yet
- Comparison of Crystal Structures Among CAAC-InGaZnO, nc-InGaZnO, and Solution-Processed InGaZnODocument4 pagesComparison of Crystal Structures Among CAAC-InGaZnO, nc-InGaZnO, and Solution-Processed InGaZnORabbi HasnatNo ratings yet
- Infrared and Raman Spectra of Inorganic and CoordiDocument1 pageInfrared and Raman Spectra of Inorganic and Coordishiva kumarNo ratings yet
- Expt 1 Chem 1 .Document45 pagesExpt 1 Chem 1 .Farhatul Abrar AnandaNo ratings yet
- Chapter13 - Acids and BasesDocument44 pagesChapter13 - Acids and BasesXiaohan TangNo ratings yet
- Chapter 10 Phase TransformationDocument26 pagesChapter 10 Phase TransformationEffendy AdipratamaNo ratings yet
- Accelerated Aging Versus Realistic Aging in Aerospace Composite Materials. V. The Effects of Hot/Wet Aging in A Structural Epoxy CompositeDocument10 pagesAccelerated Aging Versus Realistic Aging in Aerospace Composite Materials. V. The Effects of Hot/Wet Aging in A Structural Epoxy CompositeOussama El BouadiNo ratings yet
- Types of Exapnsion Devices in RAC SystemsDocument4 pagesTypes of Exapnsion Devices in RAC SystemsNishit ParmarNo ratings yet
- Desuperheating Steam: The Web TripodDocument1 pageDesuperheating Steam: The Web Tripodhappale2002No ratings yet
- Lubricants 10 00289Document11 pagesLubricants 10 00289mylover huNo ratings yet
- Yang 2013Document4 pagesYang 2013Dwi suparwatiNo ratings yet
- Xii - Chemistry (Set-3) - QPDocument9 pagesXii - Chemistry (Set-3) - QPDevanshi AwasthiNo ratings yet
- Production of Nitric Acid PDFDocument20 pagesProduction of Nitric Acid PDFPanji Aji Wibowo100% (5)
- ASSIGNMENT On FLUOROMETRY AND POLARIMETRY Pha 305 Sec-1 Group-08Document30 pagesASSIGNMENT On FLUOROMETRY AND POLARIMETRY Pha 305 Sec-1 Group-08Mahadi Hasan KhanNo ratings yet
- Exercise 1 Lab Manual Chem 117Document4 pagesExercise 1 Lab Manual Chem 117EJ FelisildaNo ratings yet
- Intertek Assay ReportDocument18 pagesIntertek Assay Reportmohsen ranjbar100% (1)