Professional Documents
Culture Documents
Activity 1.2: Approximate Roots and Powers
Uploaded by
Carlos Tadeo CapistranOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Activity 1.2: Approximate Roots and Powers
Uploaded by
Carlos Tadeo CapistranCopyright:
Available Formats
Activity 1.
2: Approximate Roots and Powers
Name ___________________________________ ID _____________ Date _____________
Use differentials to find the approximate value for
1. 16.4 6. 3 99.2
1
7. 3
2. 35.85 26
6
3. 170 8.
4.2
(3.1)
4
3 9.
4. 8.05
1
( 2.003)
5
5. 10. 1.0036
By: Arq. Monica M. Paniagua & Ing. Ziad Najjar
Use differentials and increments to solve the following
1. The radius of a circle increments from 15 to 16 centimeters. If A is the area of the circle,
estimate the change in the area. (Hint: Area of a circle is A r 2 )
2. The cost of painting a spherical shaped storage tank is of $15.00 per square meter.
Determine the change in cost for painting the tank if the radius of the tank is reduced from 3m
to 2.25m. (Hint: Surface of a sphere S 4 r 2 )
3. The size of a cubic box with a side of 8 cm is going to be modified and the new box will
have a side of 8.5 cm.
a) Find the change in the volume of the box
b) Find the approximate change in the volume of the box
4. The temperature of a coffee at room temperature, t minutes after it has been served, is
given by T = 82 - 4 t , where T is being measured in ªC
a) Find the change in the temperature of the coffee when time goes from 7 min to 8 min
b) Find the approximate change for the temperature of the coffee for the same times given in a)
5. A circular plate is going to be redesigned and its diameter will go from 50cms to 52cms
a) Find the change in the area of the plate
b) Find the approximate change in the area of the plate
By: Arq. Monica M. Paniagua & Ing. Ziad Najjar
6. A can is going to be modified in such a way that its height will change from 12cms to 12.5
cms but the diameter of the base will remain as 8cms
a) Find the change in the volume of the can
b) Find the approximate change in the volume of the can
7. The radius of a spherical balloon measures 10 inches with a possible error of 1
16
in.
Calculate the possible error in the volume of the balloon
8. The edge of a cube was found to be 30 cm. with a possible error in measurement of 0.1cm.
Estimate the maximum possible error in computing (a) the volume of the cube and (b) the
surface area.
9. A solid steel cylinder has a radius of 2.5cm. and a height of 10 cm. A tight-fitting sleeve is to
be made that will extend the radius to 2.6cm. Estimate the volume of steel needed for the
sleeve
By: Arq. Monica M. Paniagua & Ing. Ziad Najjar
You might also like
- Probe MackintoshDocument5 pagesProbe Mackintoshnrsyhira salihinNo ratings yet
- Answers Level9-10Pack3Document8 pagesAnswers Level9-10Pack3David TurnerNo ratings yet
- Solutions: MME 9602 Term Test Module I: MetalsDocument6 pagesSolutions: MME 9602 Term Test Module I: Metalszubair ahmedNo ratings yet
- SondirDocument22 pagesSondirBintang Panjaitan100% (1)
- 1.1 Reference Crop Evapotranspiration, EtoDocument20 pages1.1 Reference Crop Evapotranspiration, EtoDamalash kabaNo ratings yet
- Probe MackintoshDocument4 pagesProbe MackintoshcinterrrtotebagsNo ratings yet
- Physics QuestionsDocument7 pagesPhysics QuestionsPhilip MooreNo ratings yet
- Ece TutorialDocument7 pagesEce TutorialShreeji EnggNo ratings yet
- Probset 3 v.1Document3 pagesProbset 3 v.1Apolinario Javier KatipunanNo ratings yet
- AP Worksheet 5.1Document7 pagesAP Worksheet 5.1Koko LearNo ratings yet
- Third Summative Test in Math Vi - q3Document3 pagesThird Summative Test in Math Vi - q3Hrrym Ramirez100% (1)
- Revision SheetDocument10 pagesRevision Sheethudaalhabibi786No ratings yet
- Title:: Introduction To Sample Preparation and Optical Microscope For Metallographic ObservationDocument19 pagesTitle:: Introduction To Sample Preparation and Optical Microscope For Metallographic ObservationAmirul Shahmin B. ZubirNo ratings yet
- Claw Tooth of Mole CricketsDocument5 pagesClaw Tooth of Mole CricketsAmeer BA-faiadhNo ratings yet
- Yes PleaseDocument14 pagesYes Pleasejaime1234No ratings yet
- Preboard Day 3 February 2018Document5 pagesPreboard Day 3 February 2018Justine Marowe AustriaNo ratings yet
- Desidn AopDocument73 pagesDesidn AopDavid LambertNo ratings yet
- MDSPproblemsetDocument8 pagesMDSPproblemsetJustine SomentacNo ratings yet
- Ot 1Document12 pagesOt 1ZZROTNo ratings yet
- Mechanical Operations (CHE-205) (Makeup) (EngineeringDuniya - Com)Document3 pagesMechanical Operations (CHE-205) (Makeup) (EngineeringDuniya - Com)Cester Avila Ducusin100% (1)
- Worksheet in Measurement (Length)Document1 pageWorksheet in Measurement (Length)Kristine Marie PamorNo ratings yet
- I. Write The Letter of The Correct Answer For The Following Questions On The Blank Before The NumberDocument17 pagesI. Write The Letter of The Correct Answer For The Following Questions On The Blank Before The NumberRhenan WafooNo ratings yet
- Hot Dipped Galvanized Welded Steel PipesDocument2 pagesHot Dipped Galvanized Welded Steel PipesMuthuKumarNo ratings yet
- PET 531 Exam QuestionDocument4 pagesPET 531 Exam QuestionIgbereyivwe TejiriNo ratings yet
- 2023 June CHT206-EDocument3 pages2023 June CHT206-EGouri K SNo ratings yet
- Ikaapatnamarkahangpagsusulit 170405124948Document52 pagesIkaapatnamarkahangpagsusulit 170405124948CelCoracheaNo ratings yet
- Elective-III: Water & Waste Water Treatment: B.E. (Civil Engineering) Eighth Semester (C.B.S.)Document2 pagesElective-III: Water & Waste Water Treatment: B.E. (Civil Engineering) Eighth Semester (C.B.S.)Adesh DeshbhratarNo ratings yet
- PHY F2 End Term 1Document9 pagesPHY F2 End Term 1Selifa AbutiNo ratings yet
- Research DataDocument18 pagesResearch DataBords MoralesNo ratings yet
- 2021 04 21 Water Treatment AssignmentDocument7 pages2021 04 21 Water Treatment AssignmentchiroNo ratings yet
- Laporan Mekanika Tanah Sondir Universitas IndonesiaDocument17 pagesLaporan Mekanika Tanah Sondir Universitas IndonesiasipilPI12100% (1)
- Ball Milling - Final FinalDocument12 pagesBall Milling - Final FinalKrishna TejaNo ratings yet
- TE 1997 and 2003 Course Oct 2009Document492 pagesTE 1997 and 2003 Course Oct 2009Ajay Solate0% (1)
- Lab Manual FOR Mechanical OperationsDocument34 pagesLab Manual FOR Mechanical OperationsAdhik AgarwalNo ratings yet
- MM 361: Advanced Manufacturing: InstructionsDocument3 pagesMM 361: Advanced Manufacturing: InstructionsSimLo Lulumani Ko'osiko Taloanimae'aNo ratings yet
- 01-Oct-2012-Class7-Area and Volume PDFDocument2 pages01-Oct-2012-Class7-Area and Volume PDFkvinodan73No ratings yet
- Lab Report 1 & 2Document10 pagesLab Report 1 & 219MME-S1-323 Usman Ul Hassan PirzadaNo ratings yet
- Ce 8 Sem Elective 3 Water Waste Water Treatment Summer 2018Document2 pagesCe 8 Sem Elective 3 Water Waste Water Treatment Summer 2018Mathematics Club PCE Technical TeamNo ratings yet
- Homework Exercise - Module 1 CE231Document2 pagesHomework Exercise - Module 1 CE231Md Tanvir Haider 191-47-915No ratings yet
- CM 4002 Fluid Particle Mechanics Jun 2020Document3 pagesCM 4002 Fluid Particle Mechanics Jun 2020RAHUL MATHURNo ratings yet
- Sri Chaitanya IIT Academy., India: A Right Choice For The Real AspirantDocument19 pagesSri Chaitanya IIT Academy., India: A Right Choice For The Real AspirantPreetam Reddy BasarahalliNo ratings yet
- Calculate The Weight Loss in Steel Sample Due To Erosion Corrosion in 3.5% NaCl Solution With 10% Silica Sand Particles As Per ASTM G-184.Document11 pagesCalculate The Weight Loss in Steel Sample Due To Erosion Corrosion in 3.5% NaCl Solution With 10% Silica Sand Particles As Per ASTM G-184.Farwa NaeemNo ratings yet
- Chapter 18 Surface Area and Volume of A Cuboid and CubeDocument22 pagesChapter 18 Surface Area and Volume of A Cuboid and CubeMann GosarNo ratings yet
- Chapter 5 - Wastewater Collection and Removal ExamplesDocument13 pagesChapter 5 - Wastewater Collection and Removal ExamplesÅdän Ahmĕd DâkañeNo ratings yet
- Ot 5Document16 pagesOt 5ZZROTNo ratings yet
- Nama: Ichan M Maulana Nim: 2111141079 Kelas: S1-B Tugas Teknik Manufaktur 3Document6 pagesNama: Ichan M Maulana Nim: 2111141079 Kelas: S1-B Tugas Teknik Manufaktur 3Ichan M MaulanaNo ratings yet
- Fluid Mechanics - II (Old)Document2 pagesFluid Mechanics - II (Old)TauseefNo ratings yet
- CL 5 MathsDocument9 pagesCL 5 MathsRajkumarNo ratings yet
- Target F-2 Extra Practice 1Document28 pagesTarget F-2 Extra Practice 1alcilene almeidaNo ratings yet
- MSF 983 73Document8 pagesMSF 983 73AlbertoNo ratings yet
- Solids HomeworkDocument20 pagesSolids HomeworkindiomajaderoNo ratings yet
- Tutorial Sheet 4 - Factorial and Latin Square DesignDocument3 pagesTutorial Sheet 4 - Factorial and Latin Square DesignKaylaNo ratings yet
- Surface 2Document6 pagesSurface 2Anurag ParasharNo ratings yet
- Soil Mechanics - Problems 1Document2 pagesSoil Mechanics - Problems 1MJ ArboledaNo ratings yet
- Scientific Assistant 2018 PaperDocument20 pagesScientific Assistant 2018 PaperMeharNo ratings yet
- Name: - : Industrial Materials and ProcessesDocument3 pagesName: - : Industrial Materials and ProcessesSheryll PascobilloNo ratings yet
- Sieve Analysis of Fine & Coarse Aggregates: Cie 309 - Construction Materials Lab Lab Report 3 - Astm C136Document11 pagesSieve Analysis of Fine & Coarse Aggregates: Cie 309 - Construction Materials Lab Lab Report 3 - Astm C136Seyoung MyiouNo ratings yet
- Fecha Hora Nombre Calorias (Kcal) Carbohidratos (G)Document18 pagesFecha Hora Nombre Calorias (Kcal) Carbohidratos (G)Carlos Tadeo CapistranNo ratings yet
- Desbrosadora Sthill Fs 450 de Cuchilla: Venta: #2094497839 Cant: 1Document4 pagesDesbrosadora Sthill Fs 450 de Cuchilla: Venta: #2094497839 Cant: 1Carlos Tadeo CapistranNo ratings yet
- IEA PVPS Trends 2018 in Photovoltaic Applications PDFDocument88 pagesIEA PVPS Trends 2018 in Photovoltaic Applications PDFCarlos Tadeo CapistranNo ratings yet
- WindDocument5 pagesWindCarlos Tadeo CapistranNo ratings yet
- SolarDocument11 pagesSolarCarlos Tadeo CapistranNo ratings yet
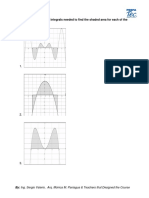
- Determine The Number of Integrals Needed To Find The Shaded Area For Each of The Following GraphsDocument2 pagesDetermine The Number of Integrals Needed To Find The Shaded Area For Each of The Following GraphsCarlos Tadeo CapistranNo ratings yet
- Carbon Bonds and HybridizationDocument12 pagesCarbon Bonds and HybridizationCarlos Tadeo CapistranNo ratings yet
- BCA Self Assessment English and TagalogDocument3 pagesBCA Self Assessment English and TagalogReymundo Pantonial Tugbong JrNo ratings yet
- Difference Between DWA and TEB Local PlannersDocument2 pagesDifference Between DWA and TEB Local PlannersChandrajit GangulyNo ratings yet
- As-St300 - Day 1 - PLC WorkingDocument16 pagesAs-St300 - Day 1 - PLC Workingashutosh123No ratings yet
- Kyehyun Park - Drawing and Painting Beautiful Flowers - Discover Techniques For Creating Realistic Florals and Plants in Pencil and Watercolor-Quarry Books (2022)Document334 pagesKyehyun Park - Drawing and Painting Beautiful Flowers - Discover Techniques For Creating Realistic Florals and Plants in Pencil and Watercolor-Quarry Books (2022)Krutika Sapkal94% (18)
- CERNCourier2021JanFeb DigitaleditionDocument33 pagesCERNCourier2021JanFeb DigitaleditionBhakti rautNo ratings yet
- IET DAVV 2014 Com2Document12 pagesIET DAVV 2014 Com2jainam dudeNo ratings yet
- Simplex 4098+seriesDocument4 pagesSimplex 4098+seriesCode JonNo ratings yet
- 2016 - Using Modern Plant Trait Relationships Between Observed and Theoretical Maximum Stomatal Conductance and Vein Density To Examine Patterns of Plant MacroevolutionDocument10 pages2016 - Using Modern Plant Trait Relationships Between Observed and Theoretical Maximum Stomatal Conductance and Vein Density To Examine Patterns of Plant MacroevolutionJuan Torres CastilloNo ratings yet
- Libros de Estructuras MetalicasDocument8 pagesLibros de Estructuras MetalicasNata277No ratings yet
- Pile CapDocument19 pagesPile Caprsdoost1345No ratings yet
- Basic Electrical Engineering: Fall 2015 Instructor: Dr. Hassan DawoodDocument34 pagesBasic Electrical Engineering: Fall 2015 Instructor: Dr. Hassan Dawoodbakhtawar saeedNo ratings yet
- Chan SHP Final-NolinksDocument3 pagesChan SHP Final-NolinksaliNo ratings yet
- Summit X670 Series: Product OverviewDocument10 pagesSummit X670 Series: Product OverviewAlex KramerNo ratings yet
- Parametric Modeling A Simple ToolDocument6 pagesParametric Modeling A Simple ToolFatimeh ShahinNo ratings yet
- Solow Model Extension-Human CapitalDocument16 pagesSolow Model Extension-Human CapitalQusay Falah Al-dalaienNo ratings yet
- Ee 434L Manual (5-12)Document45 pagesEe 434L Manual (5-12)Saleemullah KhanNo ratings yet
- Compiler Reference GuideDocument1,174 pagesCompiler Reference GuideПавел НиколаевичNo ratings yet
- Design Guide Fichtner PDFDocument246 pagesDesign Guide Fichtner PDFAnonymous knICax100% (1)
- PygmyManual v2 - 31Document67 pagesPygmyManual v2 - 31myplaxisNo ratings yet
- Res2dinvx32 PDFDocument173 pagesRes2dinvx32 PDFWahyu Sutrisno0% (1)
- Bsi Bs en 1366-8 Smoke Extraction DuctsDocument40 pagesBsi Bs en 1366-8 Smoke Extraction DuctsMUSTAFA OKSUZNo ratings yet
- Jib Cranes 20875644 Colour CatalogueDocument30 pagesJib Cranes 20875644 Colour Cataloguepsingh1996No ratings yet
- Science Spoofs, Physics Pranks and Astronomical Antics: Docslugtoast@phas - Ubc.caDocument30 pagesScience Spoofs, Physics Pranks and Astronomical Antics: Docslugtoast@phas - Ubc.cabeemanNo ratings yet
- Power World Simulator 8 TutorialDocument8 pagesPower World Simulator 8 TutorialMauricio VargasNo ratings yet
- Minggu 5 Teori AktDocument69 pagesMinggu 5 Teori AktHILDANo ratings yet
- EE145 Lab Manual Practical 6-10-12.9.19Document12 pagesEE145 Lab Manual Practical 6-10-12.9.19Viraj PatvaNo ratings yet
- Binomial Theorem: Theory and Exercise BookletDocument8 pagesBinomial Theorem: Theory and Exercise BookletEr. Narender SinghNo ratings yet
- Week 8-Wind Energy Generation - ELEC2300Document29 pagesWeek 8-Wind Energy Generation - ELEC2300Look AxxNo ratings yet
- Assignment 3Document10 pagesAssignment 3Joseph PerezNo ratings yet
- Giza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyFrom EverandGiza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyNo ratings yet
- A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceFrom EverandA Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceRating: 4 out of 5 stars4/5 (51)
- Dark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseFrom EverandDark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseRating: 3.5 out of 5 stars3.5/5 (69)
- Knocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldFrom EverandKnocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldRating: 3.5 out of 5 stars3.5/5 (64)
- A Brief History of Time: From the Big Bang to Black HolesFrom EverandA Brief History of Time: From the Big Bang to Black HolesRating: 4 out of 5 stars4/5 (2193)
- Quantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessFrom EverandQuantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessRating: 4 out of 5 stars4/5 (6)
- Packing for Mars: The Curious Science of Life in the VoidFrom EverandPacking for Mars: The Curious Science of Life in the VoidRating: 4 out of 5 stars4/5 (1396)
- Midnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterFrom EverandMidnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterRating: 4.5 out of 5 stars4.5/5 (410)
- Lost in Math: How Beauty Leads Physics AstrayFrom EverandLost in Math: How Beauty Leads Physics AstrayRating: 4.5 out of 5 stars4.5/5 (125)
- The Power of Eight: Harnessing the Miraculous Energies of a Small Group to Heal Others, Your Life, and the WorldFrom EverandThe Power of Eight: Harnessing the Miraculous Energies of a Small Group to Heal Others, Your Life, and the WorldRating: 4.5 out of 5 stars4.5/5 (54)
- The Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeFrom EverandThe Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeRating: 4.5 out of 5 stars4.5/5 (3)
- Summary and Interpretation of Reality TransurfingFrom EverandSummary and Interpretation of Reality TransurfingRating: 5 out of 5 stars5/5 (5)
- Quantum Physics: What Everyone Needs to KnowFrom EverandQuantum Physics: What Everyone Needs to KnowRating: 4.5 out of 5 stars4.5/5 (49)
- The Beginning of Infinity: Explanations That Transform the WorldFrom EverandThe Beginning of Infinity: Explanations That Transform the WorldRating: 5 out of 5 stars5/5 (60)
- The Cosmos: Exploring the Universe's Biggest MysteriesFrom EverandThe Cosmos: Exploring the Universe's Biggest MysteriesRating: 5 out of 5 stars5/5 (1)
- Beyond Weird: Why Everything You Thought You Knew about Quantum Physics Is DifferentFrom EverandBeyond Weird: Why Everything You Thought You Knew about Quantum Physics Is DifferentRating: 4 out of 5 stars4/5 (25)
- Let There Be Light: Physics, Philosophy & the Dimensional Structure of ConsciousnessFrom EverandLet There Be Light: Physics, Philosophy & the Dimensional Structure of ConsciousnessRating: 4.5 out of 5 stars4.5/5 (57)
- Black Holes: The Key to Understanding the UniverseFrom EverandBlack Holes: The Key to Understanding the UniverseRating: 4.5 out of 5 stars4.5/5 (13)
- The End of Everything: (Astrophysically Speaking)From EverandThe End of Everything: (Astrophysically Speaking)Rating: 4.5 out of 5 stars4.5/5 (157)
- The Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeFrom EverandThe Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeNo ratings yet
- Bedeviled: A Shadow History of Demons in ScienceFrom EverandBedeviled: A Shadow History of Demons in ScienceRating: 5 out of 5 stars5/5 (5)