The Integral Test

For a given series what is its sum? A corollary of the Monotonic Sequence Theorem is that the series
=1

we want to know: (1) Does it converge? (2) If it converges,

of non-

negative terms converges if and only if its partial sums are bounded from above.
Consider the harmonic series:

1 1 1 1 = 1 + + + + + . 2 3 =1 This series is divergent even though the th term 1 0 as , cf. the n-th term test seen before. However, the series has no upper bound on its partial sums. We can see this by writing the series as 1+ 1 1 1 1 1 1 1 1 1 1 + + + + + + + + + + + . 2 3 4 5 6 7 8 9 10 16

The Integral Test

Now 1 1 2 1 + > = , 3 4 4 2 1 1 1 1 4 1 + + + > = , 5 6 7 8 8 2 1 1 1 8 1 + + + > = 9 10 16 16 2

and so on. Therefore the sum of the 2 terms ending with 1 2+1 is > 2 2+1 = 1/2. Hence the sequence of partial sums is not bounded from above, and so the harmonic series diverges. Now consider the series,

1 1 1 1 1 =1+ + + + + 2 + . 2 4 9 16 =1

Does it converge or diverge? To answer this question we will consider a new approach involving the use of integration. What we need to do is compare series the integral
1/ 2 . 1 1 =1 2

with

The Integral Test

= 12 + 22 + 32 + + 2 = = 1 + 2 + 3 + + < 1 + <1+
1 1 2 1 1 1 1

1 . 1 2

Therefore < 1 +
1 1 2

=1+

1 1

= 2.

Thus < 2 for all and the partial sums are bounded from above (by 2) and therefore the series converges. Note that the series and the integral need not have the same value in the convergent case.

The Integral Test

Theorem 9: The Integral Test Let * + be a sequence of positive terms. Suppose that = (), where is a continuous, positive, decreasing function of for all ( a positive integer).
= ()

Then the series

Proof.

and the integral

both converge or diverge.

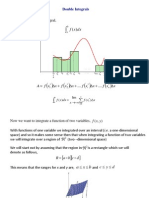
Let us consider the case = 1 and we assume that is a decreasing function with () = for every . In part (a), the areas of rectangles 1 , 2 , , enclose more area than that under the curve = () between = 1 and = + 1. Therefore we can write
+1 1

() 1 + 2 + + .

The Integral Test

From part (b), if we ignore the first rectangle, we can write

2 + 3 + + Adding the area 1 to each of the sides gives

.
1

1 + 2 + 3 + + 1 + Combining the two inequalities gives

+1 1

.
1

1 + 2 + + 1 +

.
1

These inequalities will hold as . Therefore, if

1

is finite, the right-hand part of the inequality shows that

1

is also finite. Similarly, if

part of the inequality.

is infinite, then

is infinite by the left-hand

The Integral Test

The Integral Test can be used to show that the p-series and diverges if 1. Example.
=1 1

converges if > 1

Show that the series

=1 1

(2 +1) converges by the integral test.

The function () = 1/( 2 + 1) is positive, continuous and decreasing for 1. Also

1

1 = lim ,arctan -1 = lim ,arctan arctan 1- = = 2 + 1 2 4 4

and so the series converges (but we dont know the sum).

The Ratio Test

Theorem 10: The Ratio Test Let * + be a series with positive terms and suppose that +1 lim = . Then (a) the series converges if < 1, (b) the series diverges if > 1 or is infinite, (c) the test is inconclusive if = 1. The following are cases where = 1 and test is inconclusive: 1 +1 1/( + 1) : = = 1 1/ + 1 1 : 2 +1 1/ + 1 = 1/2
2

= + 1

12 = 1.

In each case = 1 (i.e. the test is inconclusive) yet we know that

whereas 1/2 converges.

1/ diverges

The Ratio Test

Example. Use the Ratio Test to investigate the convergence of the following series: 2 + 5 ! 2 ! , , . 3 ! 2 =1 =1 =1 () 2 + 5 = , 3 +1 2+1 + 5 = 3+1

+1 (2+1 +5)/3+1 1 2+1 + 5 1 2 + 5 2 = = = (2 + 5)/3 3 2 +5 3 1 + 5 2 1 2 2 = < 1 as and the series converges. 3 1 3

The Ratio Test

() = 2 ! , ! 2 +1 = 2( + 1) ! ( + 1)! 2

+1 2 + 2 ! ! ! 2 + 2 2 + 1 = = + 1 ! + 1 ! 2 ! + 1 + 1 4 + 2 4 + 2/ = = 4 > 1 and the series diverges. + 1 1 + 1/ () ! = , +1 ( + 1)! = ( + 1)+1

+1 + 1 ! + 1 = = = + 1 +1 ! + 1 ( + 1) + 1 1 = 1 + 1/

= + 1

1 and we cannot determine the convergence or the divergence.