Professional Documents
Culture Documents
NN Ch2
Uploaded by
Prasanth ShivanandamOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
NN Ch2
Uploaded by
Prasanth ShivanandamCopyright:
Available Formats
Introduction to
Neural Networks Computing
CMSC491N/691N, Spring 2001
Notations
units:
activation/output:
if is an input unit,
for other units ,
where f( .) is the activation function for
weights:
from unit i to unit j (other books use )
j i
y x ,
j i
Y X ,
i
X signal input
i
x
j
Y ) _ (
j j
in y f y
j
Y
ji
w
ij
w
i
X
j
Y
ij
w
bias: ( a constant input)
threshold: (for units with step/threshold
activation function)
weight matrix: W={ }
i: row index; j: column index
j
b
j
ij
w
0 5 2 ( ) row vectors
3 0 4 ( )
1 6 -1 ( )
column vectors
vectors of weights:
weights come into unit j
weights go out of unit i
) (
3 , 2 , 1 j j j j
w w w w
) (
3 , 2 , 1 i i i i
w w w w
1
w
2
w
3
w
1
w
2
w
3
w
1 2 3
2
1
5
3
4
6
-1
small usually of scale the specifies
rate learning :
n) computatio vector(for input ) ...... , (
vector put target)out (or training ) ...... , (
vector input training ) ....... (
} {
raining learning/t ) ( ) (
,
2 1
2
2 , 1
ij
n
m
n
ij
ij ij ij
w
x x x x
t t t t
s s s s
w W
old w new w w
Review of Matrix Operations
Vector: a sequence of elements (the order is important)
e.g., x=(2, 1) denotes a vector
length = sqrt(2*2+1*1)
orientation angle = a
x=(x1, x2, , xn), an n dimensional vector
a point on an n dimensional space
column vector: row vector
,
_
8
5
2
1
x
a
T
x y ) 8 5 2 1 (
x x
T T
) (
X (2, 1)
transpose
norms of a vector: (magnitude)
vector operations:
i
n i
i
n
i
i
n
i
x x norm L
x x norm L
x x norm L
max
) (
1
2 / 1 2
1
2
2
1
1
1
x y
x
x
x
y y y y x
y
y
y
x x x y x
n y x
x r rx rx rx rx
T
n
n i i
n
i
n
n
T
T
n
,
_
,
_
) ... , ( ) ...... , (
dimension same of vectors column are ,
product ) dot ( inner
vector column a : , scaler a : ) ,...... , (
2
1
2 1
1
2
1
2 1
2 1
Cross product:
defines another vector orthogonal to the plan
formed by x and y.
y x
matrix:
the element on the ith row and jth column
a diagonal element
a weight in a weight matrix W
each row or column is a vector
jth column vector
ith row vector
n m
j
i
mn m m
n
n m
a
a a a
a a a
A
,
_
} {
......
......
2 1
1 12 11
,
_
m
n n m
i
j
a
a
a a A
a
a
) ...... (
:
:
1
1 x
:
:
:
ij
ii
ij
w
a
a
a column vector of dimension m is a matrix of mx1
transpose:
jth column becomes jth row
square matrix:
identity matrix:
,
_
mn n n
m
T
n m
a a a
a a a
A
......
......
2 1
1 21 11
n n
A
'
,
_
otherwise
j i if
a I
j
i
0
1
1 ...... 0 0
0 ...... 1 0
0 ..... 0 1
symmetric matrix: m = n
matrix operations:
The result is a row vector, each element of which is
an inner product of and a column vector
ji ij i i
T
a a ij or a a i or A A
, ,
) ( ) ,...... (
1
j
i n
ra ra ra rA
) ,...... (
) ,...... )( ...... (
1
1 1
n
T T
n m n m
T
a x a x
a a x x A x
T
x
j
a
product of two matrices:
vector outer product:
j i ij p m p n n m
b a C where C B A
n m n n n m
A I A
( )
,
_
,
_
n m m m
n
n
m
i
T
y x y x y x
y x y x y x
y y
x
x
x
y x
...... , ,
,...... ,
......
2 1
1 2 1 1 1
1
1
Calculus and Differential Equations
, the derivative of , with respect to time
System of differential equations
solution:
difficult to solve unless are simple
(t)
i
x
'
) ( ) (
) ( ) (
1 1
t f t x
t f t x
n n
i
x t
)) ( ), ( (
1
t x t x
n
) (t f
i
Multi-variable calculus:
partial derivative: gives the direction and speed of
change of y, with respect to
)) ( ...... ), ( ), ( ( ) (
2 1
t x t x t x f t y
n
) (
3
) (
2
2
) (
1
1
) (
2
2 1
3 2 1
3 2 1
3 2 1
3 2 1
2
) cos(
) sin(
x x x
x x x
x x x
x x x
e
x
y
e x
x
y
e x
x
y
e x x y
+ +
+ +
+ +
+ +
+ +
i
x
the total derivative:
Gradient of f :
Chain-rule: y is a function of , is a function of t
T
n
t x t x
t x t x t y
n
f
n
x
f
x
f
dt
df
) ......
1
(
......
1
) ( ) (
) ( ) ( ) (
1
) ...... , (
1 n
x
f
x
f
f
)) ( ...... ), ( ), ( ( ) (
2 1
t x t x t x f t y
n
i
x
i
x
dynamic system:
change of may potentially affect other x
all continue to change (the system evolves)
reaches equilibrium when
stability/attraction: special equilibrium point
(minimal energy state)
pattern of at a stable state often
represents a solution
'
) ...... , (
) ..... , (
1
1
1 1
) (
) (
n n
n
x x f
n
x x f
t x
t x
i
x
i x
i
0
) ...... , (
1 n
x x
i
x
Chapter 2: Simple Neural Networks for
Pattern Classification
General discussion
Linear separability
Hebb nets
Perceptron
Adaline
General discussion
Pattern recognition
Patterns: images, personal records, driving habits, etc.
Represented as a vector of features (encoded as
integers or real numbers in NN)
Pattern classification:
Classify a pattern to one of the given classes
Form pattern classes
Pattern associative recall
Using a pattern to recall a related pattern
Pattern completion: using a partial pattern to recall the
whole pattern
Pattern recovery: deals with noise, distortion, missing
information
General architecture
Single layer
net input to Y:
bias b is treated as the weight from a special unit with
constant output 1.
threshold related to Y
output
classify into one of the two classes
+
n
i
i i
w x b net
1
'
<
net
net
net f y
if 1 -
if 1
) (
Y
xn
x1
1
w
n
w
1
b
) ...... , (
1 n
x x
Decision region/boundary
n = 2, b != 0, = 0
is a line, called decision boundary, which partitions the
plane into two decision regions
If a point/pattern is in the positive region, then
, and the output is one (belongs to
class one)
Otherwise, , output 1 (belongs to
class two)
n = 2, b = 0, != 0 would result a similar partition
2
1
2
1
2
2 2 1 1
or 0
w
b
x
w
w
x
w x w x b
+ +
2
x
1
x
+
-
) , (
2 1
x x
0
2 2 1 1
+ + w x w x b
0
2 2 1 1
< + + w x w x b
If n = 3 (three input units), then the decision
boundary is a two dimensional plane in a three
dimensional space
In general, a decision boundary is a
n-1 dimensional hyper-plane in an n dimensional
space, which partition the space into two decision
regions
This simple network thus can classify a given pattern
into one of the two classes, provided one of these two
classes is entirely in one decision region (one side of
the decision boundary) and the other class is in
another region.
The decision boundary is determined completely by
the weights W and the bias b (or threshold ).
0
1
+
n
i
i i
w x b
Linear Separability Problem
If two classes of patterns can be separated by a decision boundary,
represented by the linear equation
then they are said to be linearly separable. The simple network can
correctly classify any patterns.
Decision boundary (i.e., W, b or ) of linearly separable classes can
be determined either by some learning procedures or by solving
linear equation systems based on representative patterns of each
classes
If such a decision boundary does not exist, then the two classes are
said to be linearly inseparable.
Linearly inseparable problems cannot be solved by the simple
network , more sophisticated architecture is needed.
0
1
+
n
i
i i
w x b
Examples of linearly separable classes
- Logical AND function
patterns (bipolar) decision boundary
x1 x2 y w1 = 1
-1 -1 -1 w2 = 1
-1 1 -1 b = -1
1 -1 -1 = 0
1 1 1 -1 + x1 + x2 = 0
- Logical OR function
patterns (bipolar) decision boundary
x1 x2 y w1 = 1
-1 -1 -1 w2 = 1
-1 1 1 b = 1
1 -1 1 = 0
1 1 1 1 + x1 + x2 = 0
x
o o
o
x: class I (y = 1)
o: class II (y = -1)
x
x o
x
x: class I (y = 1)
o: class II (y = -1)
Examples of linearly inseparable classes
- Logical XOR (exclusive OR) function
patterns (bipolar) decision boundary
x1 x2 y
-1 -1 -1
-1 1 1
1 -1 1
1 1 -1
No line can separate these two classes, as can be seen from
the fact that the following linear inequality system has no
solution
because we have b < 0 from
(1) + (4), and b >= 0 from
(2) + (3), which is a
contradiction
o
x o
x
x: class I (y = 1)
o: class II (y = -1)
'
< + +
+
+
<
(4)
(3)
(2)
(1)
0
0
0
0
2 1
2 1
2 1
2 1
w w b
w w b
w w b
w w b
XOR can be solved by a more complex network with
hidden units
Y
z2
z1 x1
x2
2
2
2
2
-2
-2
1
0
(-1, -1) (-1, -1) -1
(-1, 1) (-1, 1) 1
(1, -1) (1, -1) 1
(1, 1) (1, 1) -1
Hebb Nets
Hebb, in his influential book The organization of
Behavior (1949), claimed
Behavior changes are primarily due to the changes of
synaptic strengths ( ) between neurons I and j
increases only when both I and j are on: the
Hebbian learning law
In ANN, Hebbian law can be stated: increases only
if the outputs of both units and have the same
sign.
In our simple network (one output and n input units)
ij
w
ij
w
ij
w
i
x
j
y
y x old w new w w
i ij ij ij
) ( ) (
y x old w new w w
i ij ij ij
) ( ) ( or,
Hebb net (supervised) learning algorithm (p.49)
Step 0. Initialization: b = 0, wi = 0, i = 1 to n
Step 1. For each of the training sample s:t do steps 2 -4
/* s is the input pattern, t the target output of the sample */
Step 2. xi := si, I = 1 to n /* set s to input units */
Step 3. y := t /* set y to the target */
Step 4. wi := wi + xi * y, i = 1 to n /* update weight */
b := b + xi * y /* update bias */
Notes: 1) = 1, 2) each training sample is used only once.
Examples: AND function
Binary units (1, 0)
(x1, x2, 1) y=t w1 w2 b
(1, 1, 1) 1 1 1 1
(1, 0, 1) 0 1 1 1
(0, 1, 1) 0 1 1 1
(0, 0, 1) 0 1 1 1
An incorrect boundary:
1 + x1 + x2 = 0
Is learned after using
each sample once
bias unit
Bipolar units (1, -1)
It will fail to learn x1 ^ x2 ^ x3, even though the function is
linearly separable.
Stronger learning methods are needed.
Error driven: for each sample s:t, compute y from s
based on current W and b, then compare y and t
Use training samples repeatedly, and each time only
change weights slightly ( << 1)
Learning methods of Perceptron and Adaline are good
examples
(x1, x2, 1) y=t w1 w2 b
(1, 1, 1) 1 1 1 1
(1, -1, 1) -1 0 2 0
(-1, 1, 1) -1 1 1 -1
(-1, -1, 1) -1 2 2 -2
A correct boundary
-1 + x1 + x2 = 0
is successfully learned
Perceptrons
By Rosenblatt (1962)
For modeling visual perception (retina)
Three layers of units: Sensory, Association, and Response
Learning occurs only on weights from A units to R units
(weights from S units to A units are fixed).
A single R unit receives inputs from n A units (same
architecture as our simple network)
For a given training sample s:t, change weights only if the
computed output y is different from the target output t (thus
error driven)
Perceptron learning algorithm (p.62)
Step 0. Initialization: b = 0, wi = 0, i = 1 to n
Step 1. While stop condition is false do steps 2-5
Step 2. For each of the training sample s:t do steps 3 -5
Step 3. xi := si, i = 1 to n
Step 4. compute y
Step 5. If y != t
wi := wi + xi * t, i = 1 to n
b := b + * t
Notes:
-
Learning occurs only when a sample has y != t
-
Two loops, a completion of the inner loop (each sample is
used once) is called an epoch
Stop condition
-
When no weight is changed in the current epoch, or
-
When pre-determined number of epochs is reached
Informal justification: Consider y = 1 and t = -1
To move y toward t, w1should reduce net_y
If xi = 1, xi * t < 0, need to reduce w1 (xi*w1 is reduced )
If xi = -1, xi * t >0 need to increase w1 (xi*w1 is reduced )
See book (pp. 62-68) for an example of execution
Perceptron learning rule convergence theorem
Informal: any problem that can be represented by a
perceptron can be learned by the learning rule
Theorem: If there is a such that for all
P training sample patterns , then for any start
weight vector , the perceptron learning rule will
converge to a weight vector such that
for all p. ( and may not be the
same.)
Proof: reading for grad students (pp. 77-79
1
W
) ( ) ) ( (
1
p t W p x f
)} ( ), ( { p t p x
0
W
*
W
) ( ) ) ( (
*
p t W p x f
1
W
*
W
Adaline
By Widrow and Hoff (1960)
Adaptive Linear Neuron for signal processing
The same architecture of our simple network
Learning method: delta rule (another way of error driven),
also called Widrow-Hoff learning rule
The delta: t y_in
NOT t y because y = f( y_in ) is not differentiable
Learning algorithm: same as Perceptron learning except in
Step 5:
b := b + (t y_in)
wi := wi + xi * (t y_in)
Derivation of the delta rule
Error for all P samples: mean square error
E is a function of W = {w1, ... wn}
Learning takes gradient descent approach to reduce E by
modify W
the gradient of E:
There for
P
p
p in y p t
P
E
1
2
)) ( _ ) ( (
1
) ...... , (
1 n
w
E
w
E
E
i
i
w
E
w
i
P
p
P
p
i i
x p in y p t
P
p in y p t
w
p in y p t
P w
E
] )) ( _ ) ( (
2
[
) ( _ ) ( ( ))] ( _ ) ( (
2
[
1
1
i
i
w
E
w
i
P
x p in y p t
P
] )) ( _ ) ( (
2
[
1
How to apply the delta rule
Method 1 (sequential mode): change wi after each training
pattern by
Method 2 (batch mode): change wi at the end of each
epoch. Within an epoch, cumulate
for every pattern (x(p), t(p))
Method 2 is slower but may provide slightly better results
(because Method 1 may be sensitive to the sample ordering)
Notes:
E monotonically decreases until the system reaches a state
with (local) minimum E (a small change of any wi will
cause E to increase).
At a local minimum E state, , but E is not
guaranteed to be zero
i
x p in y p t )) ( _ ) ( (
i w E
i
0 /
i
x p in y p t )) ( _ ) ( (
Summary of these simple networks
Single layer nets have limited representation power
(linear separability problem)
Error drive seems a good way to train a net
Multi-layer nets (or nets with non-linear hidden units)
may overcome linear inseparability problem, learning
methods for such nets are needed
Threshold/step output functions hinders the effort to
develop learning methods for multi-layered nets
Why hidden units must be non-linear?
Multi-layer net with linear hidden layers is equivalent to a
single layer net
Because z1 and z2 are linear unit
z1 = a1* (x1*v11 + x2*v21) + b1
z1 = a2* (x1*v12 + x2*v22) + b2
y_in = z1*w1 + z2*w2
= x1*u1 + x2*u2 + b1+b2 where
u1 = (a1*v11+ a2*v12)w1, u2 = (a1*v21 + a2*v22)*w2
y_in is still a linear combination of x1 and x2.
Y
z2
z1 x1
x2
w1
w2
v11
v22
v12
v21
0
You might also like
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- Study GuideDocument66 pagesStudy GuidePrasanth ShivanandamNo ratings yet
- Ece-V-fundamentals of Cmos Vlsi (10ec56) - NotesDocument214 pagesEce-V-fundamentals of Cmos Vlsi (10ec56) - NotesNithindev Guttikonda0% (1)
- Blumix Study MaterialDocument69 pagesBlumix Study MaterialsulohitaNo ratings yet
- Cognizant PDFDocument4 pagesCognizant PDFMadan KumarNo ratings yet
- Matlab FiguresDocument2 pagesMatlab FiguresPrasanth ShivanandamNo ratings yet
- Embedded Sample PaperDocument11 pagesEmbedded Sample PaperShashi KanthNo ratings yet
- Optimization Techniques: Sources UsedDocument54 pagesOptimization Techniques: Sources UsedPrasanth ShivanandamNo ratings yet
- Sample Engineering Resume1Document2 pagesSample Engineering Resume1kanha1No ratings yet
- Ec2302 QBDocument4 pagesEc2302 QBDee PakNo ratings yet
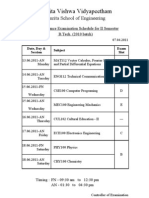
- Final Second Chance ScheduleDocument19 pagesFinal Second Chance SchedulePrasanth ShivanandamNo ratings yet
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (890)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Jamshid Ghaboussi, Xiping Steven Wu-Numerical Methods in Computational Mechanics-Taylor & Francis Group, CRC Press (2017) PDFDocument332 pagesJamshid Ghaboussi, Xiping Steven Wu-Numerical Methods in Computational Mechanics-Taylor & Francis Group, CRC Press (2017) PDFghiat100% (1)
- UT Dallas Syllabus For Math2418.001 06s Taught by Paul Stanford (phs031000)Document4 pagesUT Dallas Syllabus For Math2418.001 06s Taught by Paul Stanford (phs031000)UT Dallas Provost's Technology GroupNo ratings yet
- Ge MathsDocument2 pagesGe MathsMuhammed AthifNo ratings yet
- Quick look at vector operations in Mechanical APDLDocument29 pagesQuick look at vector operations in Mechanical APDLhazemismaeelradhi100% (1)
- dòng chảy ricciDocument97 pagesdòng chảy ricciRin TohsakaNo ratings yet
- matrixAlgebraReview PDFDocument16 pagesmatrixAlgebraReview PDFRocket FireNo ratings yet
- Levant 1993Document18 pagesLevant 1993Daniel ArevaloNo ratings yet
- MA2000 SP1 2015 Subject OutlineDocument8 pagesMA2000 SP1 2015 Subject OutlineThomasJohnnoStevensonNo ratings yet
- X-Ray Diffraction Peak Profiles From Threading Dislocations in Gan Epitaxial FilmsDocument12 pagesX-Ray Diffraction Peak Profiles From Threading Dislocations in Gan Epitaxial FilmsIlkay DemirNo ratings yet
- Us 20060073976Document31 pagesUs 20060073976cvmpatientiaNo ratings yet
- M. Krasnov, A. Kiselev, G. Makarenko, E. Shikin - Mathematical Analysis For Engineers. 1-Mir Publishers (1990)Document601 pagesM. Krasnov, A. Kiselev, G. Makarenko, E. Shikin - Mathematical Analysis For Engineers. 1-Mir Publishers (1990)Lee TúNo ratings yet
- Language FundamentalsDocument114 pagesLanguage Fundamentalssalome storeNo ratings yet
- Electromagnetics MathDocument8 pagesElectromagnetics MathBill WhiteNo ratings yet
- ISC Mathematics Class XII (Amended) - 2021Document9 pagesISC Mathematics Class XII (Amended) - 2021aditricNo ratings yet
- Appendix ThreeDocument2 pagesAppendix ThreeTom DavisNo ratings yet
- Topological Ideas BINMORE PDFDocument262 pagesTopological Ideas BINMORE PDFkishalay sarkarNo ratings yet
- Larry Smith - Linear AlgebraDocument285 pagesLarry Smith - Linear AlgebraLucas AuditoreNo ratings yet
- DPS Xii PB1 Blue Print 202324Document2 pagesDPS Xii PB1 Blue Print 202324ashu3670No ratings yet
- On Circulant MatricesDocument10 pagesOn Circulant Matricesgallantboy90No ratings yet
- 20 Days Timetable (2nd Attempt)Document2 pages20 Days Timetable (2nd Attempt)Kaustubh AggarwalNo ratings yet
- Line Plot / Line Graph : Example: Cell Phone Use in Anytowne, 1996-2002Document5 pagesLine Plot / Line Graph : Example: Cell Phone Use in Anytowne, 1996-2002Shafika NabilaNo ratings yet
- Qualifying Test - Master Programme in MathematicsDocument7 pagesQualifying Test - Master Programme in MathematicsSyedAhsanKamalNo ratings yet
- 2 Mathematics 1Document3 pages2 Mathematics 1pathir KroNo ratings yet
- Large Deflections of Microbeams Under Electrostatic LoadsDocument10 pagesLarge Deflections of Microbeams Under Electrostatic Loadsthethe308No ratings yet
- BTech EC Scheme & Syllabus 2012Document75 pagesBTech EC Scheme & Syllabus 2012kldfurio111No ratings yet
- Lecture 5Document4 pagesLecture 5Faisal RahmanNo ratings yet
- Chapter 8 (Complex Numbers)Document8 pagesChapter 8 (Complex Numbers)Naledi MashishiNo ratings yet
- Mathematics Mind MapDocument709 pagesMathematics Mind MapMike Jones100% (1)
- Javascript TutorialDocument36 pagesJavascript TutorialSiddharth ShuklaNo ratings yet
- Linear ProgrammingDocument127 pagesLinear ProgrammingLadnaksNo ratings yet