Professional Documents
Culture Documents
Heapsort: Comp 122, Spring 2004
Uploaded by
sud_mishraOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Heapsort: Comp 122, Spring 2004
Uploaded by
sud_mishraCopyright:
Available Formats
Comp 122, Spring 2004
Heapsort
heapsort - 2
Lin / Devi
Comp 122
Heapsort
Combines the better attributes of merge sort
and insertion sort.
Like merge sort, but unlike insertion sort, running
time is O(n lg n).
Like insertion sort, but unlike merge sort, sorts in
place.
Introduces an algorithm design technique
Create data structure (heap) to manage information
during the execution of an algorithm.
The heap has other applications beside sorting.
Priority Queues
heapsort - 3
Lin / Devi
Comp 122
Data Structure Binary Heap
Array viewed as a nearly complete binary tree.
Physically linear array.
Logically binary tree, filled on all levels (except lowest.)
Map from array elements to tree nodes and vice versa
Root A[1]
Left[i] A[2i]
Right[i] A[2i+1]
Parent[i] A[i/2]
length[A] number of elements in array A.
heap-size[A] number of elements in heap stored in A.
heap-size[A] s length[A]
heapsort - 4
Lin / Devi
Comp 122
Heap Property (Max and Min)
Max-Heap
For every node excluding the root,
value is at most that of its parent: A[parent[i]] > A[i]
Largest element is stored at the root.
In any subtree, no values are larger than the value
stored at subtree root.
Min-Heap
For every node excluding the root,
value is at least that of its parent: A[parent[i]] s A[i]
Smallest element is stored at the root.
In any subtree, no values are smaller than the value
stored at subtree root
heapsort - 5
Lin / Devi
Comp 122
Heaps Example
26 24 20 18 17 19 13 12 14 11
1 2 3 4 5 6 7 8 9 10
26
24 20
18
17 19 13
12
14 11
Max-heap as an
array.
Max-heap as a binary
tree.
Last row filled from left to right.
heapsort - 6
Lin / Devi
Comp 122
Height
Height of a node in a tree: the number of edges on the
longest simple downward path from the node to a leaf.
Height of a tree: the height of the root.
Height of a heap: lg n
Basic operations on a heap run in O(lg n) time
heapsort - 7
Lin / Devi
Comp 122
Heaps in Sorting
Use max-heaps for sorting.
The array representation of max-heap is not sorted.
Steps in sorting
Convert the given array of size n to a max-heap (BuildMaxHeap)
Swap the first and last elements of the array.
Now, the largest element is in the last position where it belongs.
That leaves n 1 elements to be placed in their appropriate locations.
However, the array of first n 1 elements is no longer a max-heap.
Float the element at the root down one of its subtrees so that the array
remains a max-heap (MaxHeapify)
Repeat step 2 until the array is sorted.
heapsort - 8
Lin / Devi
Comp 122
Heap Characteristics
Height = lg n
No. of leaves = n/2(
No. of nodes of
height h s n/2
h+1
(
heapsort - 9
Lin / Devi
Comp 122
Maintaining the heap property
Suppose two subtrees are max-heaps,
but the root violates the max-heap
property.
Fix the offending node by exchanging the value at the
node with the larger of the values at its children.
May lead to the subtree at the child not being a heap.
Recursively fix the children until all of them satisfy the
max-heap property.
heapsort - 10
Lin / Devi
Comp 122
MaxHeapify Example
26
14 20
24 17 19 13
12
18 11
14
14
24 24
14
14
18 18
14
MaxHeapify(A, 2)
heapsort - 11
Lin / Devi
Comp 122
Procedure MaxHeapify
MaxHeapify(A, i)
1. l left(i)
2. r right(i)
3. if l s heap-size[A] and A[l] > A[i]
4. then largest l
5. else largest i
6. if r s heap-size[A] and A[r] > A[largest]
7. then largest r
8. if largest= i
9. then exchange A[i] A[largest]
10. MaxHeapify(A, largest)
Assumption:
Left(i) and Right(i)
are max-heaps.
heapsort - 12
Lin / Devi
Comp 122
Running Time for MaxHeapify
MaxHeapify(A, i)
1. l left(i)
2. r right(i)
3. if l s heap-size[A] and A[l] > A[i]
4. then largest l
5. else largest i
6. if r s heap-size[A] and A[r] > A[largest]
7. then largest r
8. if largest= i
9. then exchange A[i] A[largest]
10. MaxHeapify(A, largest)
Time to fix node i and
its children = O(1)
Time to fix the
subtree rooted at one
of is children =
T(size of subree at
largest)
PLUS
heapsort - 13
Lin / Devi
Comp 122
Running Time for MaxHeapify(A, n)
T(n) = T(largest) + O(1)
largest s 2n/3 (worst case occurs when the last row of
tree is exactly half full)
T(n) s T(2n/3) + O(1) T(n) = O(lg n)
Alternately, MaxHeapify takes O(h) where h is the
height of the node where MaxHeapify is applied
heapsort - 14
Lin / Devi
Comp 122
Building a heap
Use MaxHeapify to convert an array A into a max-heap.
How?
Call MaxHeapify on each element in a bottom-up
manner.
BuildMaxHeap(A)
1. heap-size[A] length[A]
2. for i length[A]/2 downto 1
3. do MaxHeapify(A, i)
heapsort - 15
Lin / Devi
Comp 122
BuildMaxHeap Example
24 21 23 22 36 29 30 34 28 27
Input Array:
24
21 23
22
36 29 30
34
28 27
Initial Heap:
(not max-heap)
heapsort - 16
Lin / Devi
Comp 122
BuildMaxHeap Example
24
21 23
22
36 29 30
34
28 27
MaxHeapify(10/2 = 5)
36 36
MaxHeapify(4)
22 34
22
MaxHeapify(3)
23 30
23
MaxHeapify(2)
21 36
21
MaxHeapify(1)
24 36
24 34
24 28
24
21
21
27
heapsort - 17
Lin / Devi
Comp 122
Correctness of BuildMaxHeap
Loop Invariant: At the start of each iteration of the for
loop, each node i+1, i+2, , n is the root of a max-heap.
Initialization:
Before first iteration i = n/2
Nodes n/2+1, n/2+2, , n are leaves and hence roots of
max-heaps.
Maintenance:
By LI, subtrees at children of node i are max heaps.
Hence, MaxHeapify(i) renders node i a max heap root (while
preserving the max heap root property of higher-numbered
nodes).
Decrementing i reestablishes the loop invariant for the next
iteration.
heapsort - 18
Lin / Devi
Comp 122
Running Time of BuildMaxHeap
Loose upper bound:
Cost of a MaxHeapify call No. of calls to MaxHeapify
O(lg n) O(n) = O(nlg n)
Tighter bound:
Cost of a call to MaxHeapify at a node depends on the height,
h, of the node O(h).
Height of most nodes smaller than n.
Height of nodes h ranges from 0 to lg n.
No. of nodes of height h is n/2
h+1
(
heapsort - 19
Lin / Devi
Comp 122
Running Time of BuildMaxHeap
|
.
|
\
|
=
(
(
(
=
=
+
n
h
h
n
h
h
h
n O
h O
n
lg
0
lg
0
1
2
) (
2
2
) 2 / 1 1 (
2 / 1
(A.8) in 2 / 1 ,
2
2
2
0
lg
0
=
=
= s
=
=
x
h
h
h
h
n
h
h
) (
2 2
0
lg
0
n O
h
n O
h
n O
h
h
n
h
h
=
|
.
|
\
|
= |
.
|
\
|
= =
Tighter Bound for T(BuildMaxHeap)
T(BuildMaxHeap)
Can build a heap from an unordered array in linear time
heapsort - 20
Lin / Devi
Comp 122
Heapsort
Sort by maintaining the as yet unsorted elements as a
max-heap.
Start by building a max-heap on all elements in A.
Maximum element is in the root, A[1].
Move the maximum element to its correct final
position.
Exchange A[1] with A[n].
Discard A[n] it is now sorted.
Decrement heap-size[A].
Restore the max-heap property on A[1..n1].
Call MaxHeapify(A, 1).
Repeat until heap-size[A] is reduced to 2.
heapsort - 21
Lin / Devi
Comp 122
Heapsort(A)
HeapSort(A)
1. Build-Max-Heap(A)
2. for i length[A] downto 2
3. do exchange A[1] A[i]
4. heap-size[A] heap-size[A] 1
5. MaxHeapify(A, 1)
heapsort - 22
Lin / Devi
Comp 122
Heapsort Example
26 24 20 18 17 19 13 12 14 11
1 2 3 4 5 6 7 8 9 10
26
24 20
18
17 19 13
12
14 11
heapsort - 23
Lin / Devi
Comp 122
Algorithm Analysis
In-place
Not Stable
Build-Max-Heap takes O(n) and each of the n-1 calls
to Max-Heapify takes time O(lg n).
Therefore, T(n) = O(n lg n)
HeapSort(A)
1. Build-Max-Heap(A)
2. for i length[A] downto 2
3. do exchange A[1] A[i]
4. heap-size[A] heap-size[A] 1
5. MaxHeapify(A, 1)
heapsort - 24
Lin / Devi
Comp 122
Heap Procedures for Sorting
MaxHeapify O(lg n)
BuildMaxHeap O(n)
HeapSort O(n lg n)
heapsort - 25
Lin / Devi
Comp 122
Priority Queue
Popular & important application of heaps.
Max and min priority queues.
Maintains a dynamic set S of elements.
Each set element has a key an associated value.
Goal is to support insertion and extraction efficiently.
Applications:
Ready list of processes in operating systems by their
priorities the list is highly dynamic
In event-driven simulators to maintain the list of events to be
simulated in order of their time of occurrence.
heapsort - 26
Lin / Devi
Comp 122
Basic Operations
Operations on a max-priority queue:
Insert(S, x) - inserts the element x into the set S
S S {x}.
Maximum(S) - returns the element of S with the largest key.
Extract-Max(S) - removes and returns the element of S with
the largest key.
Increase-Key(S, x, k) increases the value of element xs key
to the new value k.
Min-priority queue supports Insert, Minimum, Extract-
Min, and Decrease-Key.
Heap gives a good compromise between fast insertion
but slow extraction and vice versa.
heapsort - 27
Lin / Devi
Comp 122
Heap Property (Max and Min)
Max-Heap
For every node excluding the root,
value is at most that of its parent: A[parent[i]] > A[i]
Largest element is stored at the root.
In any subtree, no values are larger than the value
stored at subtree root.
Min-Heap
For every node excluding the root,
value is at least that of its parent: A[parent[i]] s A[i]
Smallest element is stored at the root.
In any subtree, no values are smaller than the value
stored at subtree root
heapsort - 28
Lin / Devi
Comp 122
Heap-Extract-Max(A)
Heap-Extract-Max(A)
1. if heap-size[A] < 1
2. then error heap underflow
3. max A[1]
4. A[1] A[heap-size[A]]
5. heap-size[A] heap-size[A] - 1
6. MaxHeapify(A, 1)
7. return max
Running time : Dominated by the running time of MaxHeapify
= O(lg n)
Implements the Extract-Max operation.
heapsort - 29
Lin / Devi
Comp 122
Heap-Insert(A, key)
Heap-Insert(A, key)
1. heap-size[A] heap-size[A] + 1
2. i heap-size[A]
4. while i > 1 and A[Parent(i)] < key
5. do A[i] A[Parent(i)]
6. i Parent(i)
7. A[i] key
Running time is O(lg n)
The path traced from the new leaf to the root has
length O(lg n)
heapsort - 30
Lin / Devi
Comp 122
Heap-Increase-Key(A, i, key)
Heap-Increase-Key(A, i, key)
1 If key < A[i]
2 then error new key is smaller than the current key
3 A[i] key
4 while i > 1 and A[Parent[i]] < A[i]
5 do exchange A[i] A[Parent[i]]
6 i Parent[i]
Heap-Insert(A, key)
1 heap-size[A] heap-size[A] + 1
2 A[heap-size[A]]
3 Heap-Increase-Key(A, heap-size[A], key)
heapsort - 31
Lin / Devi
Comp 122
Examples
You might also like
- 08 HeapsortDocument31 pages08 HeapsortGireeshma ReddyNo ratings yet
- Heapsort: Comp 122, Spring 2004Document31 pagesHeapsort: Comp 122, Spring 2004Ioannis MilasNo ratings yet
- Sorting and Order Statistics (1x1)Document107 pagesSorting and Order Statistics (1x1)Miki MicahNo ratings yet
- Heap SortDocument40 pagesHeap SortaggarwalmeghaNo ratings yet
- Introduction To Algorithms: Courtesy of MIT Press. Used With PermissionDocument28 pagesIntroduction To Algorithms: Courtesy of MIT Press. Used With PermissionPranav KarthikeyanNo ratings yet
- Chapter 6 HeapsortDocument12 pagesChapter 6 HeapsortAYUSHI NIGAMNo ratings yet
- Spring 2021: Data Structures 2Document15 pagesSpring 2021: Data Structures 2AbazNo ratings yet
- Ranjithkumar.s (DSA Theory DA1)Document7 pagesRanjithkumar.s (DSA Theory DA1)RANJITHKUMAR SNo ratings yet
- 373 Lecture 3Document25 pages373 Lecture 3api-3696125No ratings yet
- Heap Sort N File HandlingDocument17 pagesHeap Sort N File HandlingRISHITANo ratings yet
- Unit 2 SortingDocument42 pagesUnit 2 SortingknoxxNo ratings yet
- 5 Lec HeapfinalDocument25 pages5 Lec HeapfinalHarshit RoyNo ratings yet
- Lecture 06 - HeapSortDocument42 pagesLecture 06 - HeapSortSyed Nasir DanialNo ratings yet
- H9-Solution (WWW Alirezaweb Com) PDFDocument3 pagesH9-Solution (WWW Alirezaweb Com) PDFVahid EsmaeilzadehNo ratings yet
- Heap SortDocument39 pagesHeap SortAkash JainNo ratings yet
- Spring 2019 Data Structures II #2Document20 pagesSpring 2019 Data Structures II #2AbazNo ratings yet
- Heap SortDocument38 pagesHeap SortnurulalomadorNo ratings yet
- CS 332: Algorithms: Introduction To HeapsortDocument35 pagesCS 332: Algorithms: Introduction To HeapsortAnonymous niE5VQOHNo ratings yet
- Analysis of HeapsortDocument37 pagesAnalysis of HeapsortFrancisco Marlito Muñoz AlforqueNo ratings yet
- CLRSCH 6 SlidesDocument14 pagesCLRSCH 6 Slidessanjayjain.nitkNo ratings yet
- Chapter-8. HeapDocument11 pagesChapter-8. HeapQuazi Hasnat IrfanNo ratings yet
- Outline: - Heap Data Structure - Extract Min - Insert - Priority Queue - HeapsortDocument3 pagesOutline: - Heap Data Structure - Extract Min - Insert - Priority Queue - HeapsortJuan RamírezNo ratings yet
- A2SV - Heap LectureDocument87 pagesA2SV - Heap Lecturefedasa.boteNo ratings yet
- Heaps, Heapsort, Priority QueuesDocument13 pagesHeaps, Heapsort, Priority Queueshim7827No ratings yet
- 1 Heaps: 1.1 The Heap Data StructureDocument8 pages1 Heaps: 1.1 The Heap Data StructureSelenia Ramirez ReyesNo ratings yet
- Adc 4Document61 pagesAdc 4ati atiNo ratings yet
- One Minute Review of Basic Data Structures: DictionariesDocument14 pagesOne Minute Review of Basic Data Structures: Dictionariesnamithaa kNo ratings yet
- 1 Heaps: 1.1 The Heap Data StructureDocument8 pages1 Heaps: 1.1 The Heap Data Structureshashank dwivediNo ratings yet
- Heap SortDocument10 pagesHeap SorthbNo ratings yet
- Faculty of Engineering & Technology: Assistant Professor Computer Science & EngineeringDocument21 pagesFaculty of Engineering & Technology: Assistant Professor Computer Science & EngineeringPayal MishraNo ratings yet
- Implementation and Runtime Analysis of Heap SortDocument6 pagesImplementation and Runtime Analysis of Heap SortEayashen ArafatNo ratings yet
- CS2040 Tutorial5 AnsDocument4 pagesCS2040 Tutorial5 Ansjoanna tayNo ratings yet
- Unit 2: Sorting and Order Statistics: Course ContentsDocument33 pagesUnit 2: Sorting and Order Statistics: Course ContentshrsliNo ratings yet
- LectureSeven2020 Heap PDFDocument4 pagesLectureSeven2020 Heap PDFMehul RathoreNo ratings yet
- Heap SortDocument5 pagesHeap Sortdhiraj1223353No ratings yet
- HeapSort in Real - TimeDocument5 pagesHeapSort in Real - TimeRadheshyam NayakNo ratings yet
- M. Santosh Kumar Datastructures Using C++Document7 pagesM. Santosh Kumar Datastructures Using C++Marumamula Santosh KumarNo ratings yet
- 1/1-A For Unsuccessful, 1/a Log (1/1-A) For Successful SearchDocument3 pages1/1-A For Unsuccessful, 1/a Log (1/1-A) For Successful SearchRobertSmithNo ratings yet
- CSC 263Document17 pagesCSC 263hitman047No ratings yet
- Chapter 8 - HeapsDocument41 pagesChapter 8 - HeapsNguyễn Thanh LinhNo ratings yet
- Heap Sort Algorithm: Relationship Between Array Indexes and Tree ElementsDocument15 pagesHeap Sort Algorithm: Relationship Between Array Indexes and Tree ElementsMudit ChoudharyNo ratings yet
- Data Structures and Algorithms (AT70.02)Document15 pagesData Structures and Algorithms (AT70.02)mellyNo ratings yet
- Heap SortDocument8 pagesHeap SortVimal PrakashNo ratings yet
- Adsa-2unit Heap ContinueDocument20 pagesAdsa-2unit Heap Continuesharmilahema33No ratings yet
- Lec 06 HeapsortDocument20 pagesLec 06 Heapsortcoco finaNo ratings yet
- HeapAndHeapsort PDFDocument12 pagesHeapAndHeapsort PDFLoai LabaniNo ratings yet
- AlgorithmDocument18 pagesAlgorithmRaja shreeNo ratings yet
- H170227e Vimbainashe Chigumbu Daa-3Document8 pagesH170227e Vimbainashe Chigumbu Daa-3Vimbainashe ChigumbuNo ratings yet
- Heap (Data Structure)Document7 pagesHeap (Data Structure)Andres R. BucheliNo ratings yet
- Heap TreesDocument24 pagesHeap TreesSai KrishnaNo ratings yet
- Daa Lab Manual Kcs553 2022-23Document89 pagesDaa Lab Manual Kcs553 2022-232030195No ratings yet
- Priority Queues (Heaps)Document56 pagesPriority Queues (Heaps)bhavana1203No ratings yet
- Heap Sort - JavatpointDocument16 pagesHeap Sort - JavatpointAakash SolankiNo ratings yet
- HEAP SORT NewDocument8 pagesHEAP SORT Newaarti46858No ratings yet
- Cs-509: Advanced Data Structures and Algorithms: Assignment Number 3Document7 pagesCs-509: Advanced Data Structures and Algorithms: Assignment Number 3Balpreet SinghNo ratings yet
- Heap SortDocument38 pagesHeap SortreemNo ratings yet
- Heap and Priority Queue: Li Yin February 6, 2019Document12 pagesHeap and Priority Queue: Li Yin February 6, 2019markNo ratings yet
- Ads Unit IIIDocument18 pagesAds Unit IIIrajasekharv86No ratings yet
- DAA-C3-Heap For Prim'sDocument7 pagesDAA-C3-Heap For Prim'samanterefe99No ratings yet
- Data Structures and Algorithms in Swift: Implement Stacks, Queues, Dictionaries, and Lists in Your AppsFrom EverandData Structures and Algorithms in Swift: Implement Stacks, Queues, Dictionaries, and Lists in Your AppsNo ratings yet
- Esiee MimoDocument52 pagesEsiee Mimosud_mishraNo ratings yet
- Feb2010 9471 MME R2 0 CPLDocument54 pagesFeb2010 9471 MME R2 0 CPLsud_mishraNo ratings yet
- Agilent Illustration of An FDDDocument15 pagesAgilent Illustration of An FDDsud_mishraNo ratings yet
- RRCDocument27 pagesRRCsud_mishraNo ratings yet
- 22 Safavi EhDocument26 pages22 Safavi EhghionoiucNo ratings yet
- Wireless-Networks-Lte Advanced Evolving and Expanding Into New Frontiers.v11.20140304Document42 pagesWireless-Networks-Lte Advanced Evolving and Expanding Into New Frontiers.v11.20140304Datacom Engr Rashid ShahNo ratings yet
- Overview of The 3GPP LTE Physical LayerDocument27 pagesOverview of The 3GPP LTE Physical Layersomeone409008100% (5)
- LTE Advance REV 090003 r1Document48 pagesLTE Advance REV 090003 r1matrix121985100% (1)
- Introduction To Wireless MIMO - Theory and ApplicationsDocument63 pagesIntroduction To Wireless MIMO - Theory and Applicationskokusz76100% (2)
- MIMO RohdeDocument23 pagesMIMO RohdeRenato De LaraNo ratings yet
- WWW Sharetechnote Com HTML FromR99toLTEDocument38 pagesWWW Sharetechnote Com HTML FromR99toLTEsud_mishraNo ratings yet
- Lte Attach PDFDocument6 pagesLte Attach PDFNitin KatariaNo ratings yet
- 1MA96 0E WiMAXDocument34 pages1MA96 0E WiMAXsud_mishraNo ratings yet
- 1MA96 0E WiMAXDocument34 pages1MA96 0E WiMAXsud_mishraNo ratings yet
- Intro To LTEDocument78 pagesIntro To LTEAndrea StefanelliNo ratings yet
- 3GPP Beijing Workshop Courau TSG RAN ChairmanDocument30 pages3GPP Beijing Workshop Courau TSG RAN Chairmansud_mishraNo ratings yet
- Lte - Basics CallDocument87 pagesLte - Basics CallAvi ShettyNo ratings yet
- Lecture 20Document26 pagesLecture 20sud_mishraNo ratings yet
- 12 Umts-EdchDocument32 pages12 Umts-EdchAjay Parmar100% (1)
- RRCDocument27 pagesRRCsud_mishraNo ratings yet
- LTEDocument22 pagesLTEsud_mishraNo ratings yet
- 3GPP LTE (Long Term Evolution) : University of Kansas - School of EngineeringDocument39 pages3GPP LTE (Long Term Evolution) : University of Kansas - School of Engineeringخالد ياسر مواسNo ratings yet
- GMAT+Tactical+Strategies+V1 1Document52 pagesGMAT+Tactical+Strategies+V1 1sud_mishraNo ratings yet
- LTE RRC Connection Setup MessagingDocument10 pagesLTE RRC Connection Setup MessagingNagasravika BodapatiNo ratings yet
- Mobility Management in UMTSDocument27 pagesMobility Management in UMTSFaisal KhanNo ratings yet
- V HDL TutorialDocument74 pagesV HDL Tutorialanmol123454No ratings yet
- 3GPP LTE MAC PresentationDocument23 pages3GPP LTE MAC PresentationEventHelix.comNo ratings yet
- LTE Protocol SignalingDocument11 pagesLTE Protocol SignalingKhåïrul Akmar TiminNo ratings yet
- MIMO in LTE Operation and MeasurementDocument25 pagesMIMO in LTE Operation and MeasurementpetersoteNo ratings yet
- 10 UE-modesDocument11 pages10 UE-modesibrar1137No ratings yet
- Heapsort AlgoDocument16 pagesHeapsort AlgoMudit ChoudharyNo ratings yet
- HeapSort in Real - TimeDocument5 pagesHeapSort in Real - TimeRadheshyam NayakNo ratings yet
- Of Engineering & Technology, Coimbatore of Engineering & Technology, CoimbatoreDocument1 pageOf Engineering & Technology, Coimbatore of Engineering & Technology, CoimbatoreNithya SubramanianNo ratings yet
- Heap SortDocument29 pagesHeap SortamanNo ratings yet
- Binomial HeapDocument16 pagesBinomial HeapNishant MishraNo ratings yet
- Min Max HeapsDocument22 pagesMin Max HeapsyashikabirdiNo ratings yet
- Heap SortDocument3 pagesHeap SortByronPérezNo ratings yet
- Fibonacci Heaps: These Lecture Slides Are Adapted From CLRS, Chapter 20Document46 pagesFibonacci Heaps: These Lecture Slides Are Adapted From CLRS, Chapter 20Raghuveer RamanNo ratings yet
- Heap Data StructureDocument5 pagesHeap Data StructureISR EducationsNo ratings yet
- Uses A Heap As Its Data Structure - In-Place Sorting Algorithm - Memory Efficient - Time Complexity - O (N Log (N) )Document41 pagesUses A Heap As Its Data Structure - In-Place Sorting Algorithm - Memory Efficient - Time Complexity - O (N Log (N) )mvdurgadeviNo ratings yet
- Leftist Skew HeapsDocument52 pagesLeftist Skew HeapsRevathy100% (1)
- Leftist Skew HeapsDocument52 pagesLeftist Skew HeapsKeyan Monadjem100% (1)
- Binomial Heaps: 15-211 Fundamental Structures of Computer ScienceDocument24 pagesBinomial Heaps: 15-211 Fundamental Structures of Computer ScienceraulNo ratings yet
- Michelle Bodnar, Andrew Lohr May 22, 2017: H h+1 H 1 I 0 I HDocument16 pagesMichelle Bodnar, Andrew Lohr May 22, 2017: H h+1 H 1 I 0 I HAbhishek SinghNo ratings yet
- 06 1 Priority Queues 2 HeapsDocument152 pages06 1 Priority Queues 2 Heapskunal lahotiNo ratings yet
- Lecture-08 - Advanced Data Structures - 2Document56 pagesLecture-08 - Advanced Data Structures - 2灭霸No ratings yet
- Presentation On HeapsortDocument23 pagesPresentation On Heapsortabhics006100% (1)
- Leftist Heaps and Skew HeapsDocument13 pagesLeftist Heaps and Skew HeapsLeming ShenNo ratings yet
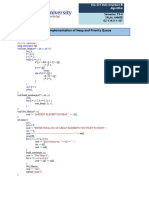
- Lab 11: Implementation of Heap and Priority QueueDocument3 pagesLab 11: Implementation of Heap and Priority QueuenasirqureshiNo ratings yet
- Binary Heaps, Heap Sort Algorithm: Welcome To CS221: Programming & Data StructuresDocument44 pagesBinary Heaps, Heap Sort Algorithm: Welcome To CS221: Programming & Data StructuresPRITAM RAJNo ratings yet
- Heap Data Structure - Interview CakeDocument15 pagesHeap Data Structure - Interview CakeRonaldMartinezNo ratings yet
- Pairing HeapsDocument31 pagesPairing Heapsmanishbhardwaj81310% (1)
- 1) Write A Program For Heap Sort? Ans: #IncludeDocument8 pages1) Write A Program For Heap Sort? Ans: #IncludeUtpal RaiNo ratings yet
- Bakhtawar AssignmentDocument6 pagesBakhtawar AssignmentMASTER JIINo ratings yet
- Insertion, Deletion, Sorting and Complexity AnalysisDocument10 pagesInsertion, Deletion, Sorting and Complexity AnalysisSudha ShankerNo ratings yet
- Name - Aryan Gupta Reg. No. 199301088 Section - BDocument9 pagesName - Aryan Gupta Reg. No. 199301088 Section - BbruhNo ratings yet
- Lecture 6 Algorithms and Problem SolvingDocument29 pagesLecture 6 Algorithms and Problem SolvingEmad AbdelkaderNo ratings yet
- 6.006 Introduction To Algorithms: Mit OpencoursewareDocument7 pages6.006 Introduction To Algorithms: Mit Opencoursewareraw.junkNo ratings yet
- Heap AlgorithmDocument6 pagesHeap AlgorithmMaysam AlkeramNo ratings yet
- Mergeable HeapsDocument27 pagesMergeable HeapsSitmCompSansthanNo ratings yet